2024年バージョンの全面改定された新しい本が公開されているので移動してください

関数型プログラミングをゼロからわかりやすく実用的に幅広い視点から解説！〜 圏論からFRPの構築まで

a岡部　健Ken Okabekentutorialbook@gmail.com 関数型プログラミングが『銀の弾丸』である　という非常識な常識 2022Functional Programming as the Silver bullet, that is the Insane common sense 2022

関数型プログラミング（Functional programming）を解説します。

New!【ReactのためのFRP（ReactiveMonad）のDemo その他】の章を最後に追加しました 1. 何が問題なのだろう？ 2. 命令型プログラミング＝ほぼすべてのプログラミング入門者が半ば強制的に辿る道 2.1. Start from Scratch（ゼロからのスタート） 2.2. 命令型コード(JavaScript) 2.3. 命令型プログラミングに傾倒している「歪な状況」を根本的に解決する必要がある 3. 関数型プログラミング（Functional Programming）は式（Expression）の組み立て 3.1. 関数型コード(JavaScript) 3.2. 関数型コードは式（Expression）である 3.3. 関数型プログラミングは式（Expression）を組み立てていく作業 3.4. 関数型コードは値が変化するようなことはない 4. 関数と二項演算子　関数型コードの式を構成する主要部品 4.1. 関数（Function）と二項演算子（Binary operator） 4.2. 関数（Function）と演算子（Operator）は本当は同じものである 4.3. 二項演算子（Binary operator）はとてつもなく強力な記法である 5. オブジェクト指向のメソッドを関数型の二項演算子として置き換える 5.1. 関数型＆オブジェクト指向のハイブリッド言語としてのJavaScript 5.2. オブジェクト指向時代の終焉 5.3. オブジェクト指向のメソッドと二項演算の関係 5.4. JavaScriptで独自の二項演算子（Custom operator）を定義する 5.5. 既存のオブジェクトメソッドを二項演算子として捉え直す 6. 式の組み立ては依存グラフの構成 6.1. もっとも単純な関数型コード 6.2. 少し複雑な関数型コード 6.3. 依存グラフ（Dependency graph）を構成する式（関数型コード）を書いてコンピュータに解決してもらう 6.4. 計算不可能な巡回グラフ 有向閉路グラフ (directed cycle graph) 6.5. 計算可能な有向非巡回グラフ（DAG） 6.6. 命令型プログラミングのフローをコントロールする文（Statement）は完全に不要だった　数式でやれば良い 6.7. 二項演算'reduce'の振る舞いの謎 6.8. 依存グラフを構成する二項演算を最大限に活用した式の組み立て 7. 命令型コードのif文switch文は場合分けの演算式にする 7.1. 命令型コードのif文 7.2. 関数型コードのif式 7.3. 条件 (三項) 演算子をつかう 7.4. より洗練され強力なパターンマッチングをつかう 7.5. 【余談】TC39の没落 8. 関数型プログラミングで複雑性との闘いに勝利するためのたったひとつの方法 8.1. ある式を別の式に交換する 8.2. 「等しい（Equality）」という超強力な概念 8.3. ソフトウェア危機に対する工学的アプローチの根本的な問題 8.4. 『銀の弾丸』等しくすれば組合せ爆発（Combinatorial explosion）を回避可能 9. 型（Type）は何故そんなに役に立つのか？そもそも型（Type）とは何か？ 9.1. JavaScriptコミュニティでは型（Type）が圧倒的に重要視されている 9.2. 巷によくある、よくわからない、型（Type）の説明 9.3. わかりやすい、型（Type）の説明 9.4. スーパーイディオム 10. 関数（Function） 10.1. 関数の具体例 10.2. かんたんにテーブルで表される関数 10.3. テーブルからかんたんにグラフにできる関数 10.4. 数学法則を使う関数 10.5. 数式だけが関数なのではない 11. 写像（Map） 11.1. 写像（Map）という概念の定義 11.2. 写像（Map）と集合（Set）と型（Type） 11.3. 型（type）集合（set）写像（map）関数（function）定義域（domain）値域（range）終域（codomain） 12. 関数の表記法 12.1. f(x) 記法とアロー記法 12.2. プレースホルダ（placeholder）という概念 12.3. f(x) 記法の関数の定義 12.4. f(x) 記法の関数の適用 12.5. f(x) 記法でもアロー記法でもない関数の定義 12.6. アロー記法の関数の定義 12.7. アロー記法の関数の適用 13. f(x) 記法からの脱却　パイプライン演算子（Pipeline Operator） 13.1. f(x) 記法の問題点 13.2. データファーストになるパイプ構造 13.3. 独自のパイプライン演算子をJavaScriptで実装する試み 13.4. 関数（写像）の連鎖をイメージ通りに表現できるパイプライン演算子 13.5. 二項演算子で式を書けばコードはシンプルになりType定義の構造と一致しやすい 13.6. 二項演算子（Custom operator）は見やすくて書きやすい 14. 代数構造（代数的構造）（Algebraic structure）と有向非巡回グラフ（DAG）＝依存グラフ 14.1. これまでのまとめ 14.2. Twitterは代数構造と有向非巡回グラフ（DAG）＝依存グラフを活用して自社システムを組んでいる 14.3. 代数構造（代数的構造）（Algebraic structure） 14.4. ３つの代数構造と「等しい（Equality）」という概念 15. モノイド（Monoid）複雑性を排除してくれるシンプルな二項演算 15.1. モノイド（Monoid）の具体例 15.2. モノイド（Monoid）の定義 15.3. モノイドの素晴らしさ①　型（Type）が単一の閉じた二項演算 15.4. モノイドの素晴らしさ②　組み合わせ方に依存しない、結合法則（Associativity） 15.5. モノイドの素晴らしさ③　単位元（Identity element） 15.6. 半群（Semigroup）にはいつでも単位元を追加してモノイドにできる 15.7. モノイドとFold（Reduce）の強力さ 15.8. Fold（Reduce）と単位元 15.9. 論理演算もモノイド 16. 関数（写像）の連鎖と関数（写像）の合成（Function composition） 16.1. 関数（写像）の連鎖 16.2. 関数（写像）の合成（Function composition） 16.3. 関数（写像）合成（Function composition）は二項演算 16.4. 関数（写像）合成（Function composition）はモノイド（Monoid） 16.5. 関数の合成という二項演算には結合性がある 16.6. 関数の合成という二項演算には左右の単位元が存在する 16.7. 関数合成という二項演算はモノイド（証明終わり） 17. 高階関数（Higher-order function） 17.1. 関数の合成（Function compositon）と高階関数（Higher-order function）という用語 17.2. 高階関数（Higher-order function）は世界にありふれている 17.3. パイプライン演算子をつかって高階関数を表現する 17.4. 関数の合成（Function compositon）と高階関数（Higher-order function）の比較 17.5. 関数同士の組み合わせでない高階関数 17.6. 高階関数（Higher-order function）とラムダ式（アロー関数式） 17.7. ラムダ式（アロー関数式）で遊ぶ identity関数 17.8. ラムダ式（アロー関数式）で遊ぶ right関数 17.9. ラムダ式（アロー関数式）で遊ぶ log関数 17.10. right関数で命令型コードの順次実行をエミュレートしてしまう 17.11. コンビネータ論理 17.12. 2+引数関数は使わず単項関数（Unary function）を使う　 17.13. カリー化(currying) 17.14. カリー化(currying)する関数とアン・カリー化（uncurrying）する関数 18. 独自の二項演算（Custom operator）、関数合成の二項演算子、パイプライン演算子の実装 18.1. 道具立てを揃える 18.2. JavaScriptで独自の二項演算子（Custom operator）を定義する 18.3. JavaScriptで独自の二項演算子（Custom operator）を定義するための関数 18.4. 関数合成の二項演算子の実装　グローバル 18.5. 関数合成の二項演算子の実装　ローカル 18.6. パイプライン演算子の実装 18.7. null問題とオプション型（OptionType） 18.8. パイプライン演算子のコード 19. ファンクタ（Functor）すべてを包括するような代数構造 19.1. モノイド（Monoid）と同じくらい重要なファンクタ（Functor）という代数構造 19.2. ファンクタ（Functor）すべてを包括するような代数構造 19.3. Array.map()というファンクタ（Functor）を調べればわかってくること 19.4. パイプライン演算（Pipeline operation）は Identity functor 19.5. FunctorはIdentity functor（関数適用）を基本とする拡張可能な代数構造 19.6. Functorをもっと厳密にTypeScriptで定義していく 19.7. 圏論（Category theory）のFunctor 20. モナド（Monad）はファンクタ（Functor）の特別なケース 20.1. パイプライン演算は関数合成（Function composition）ができる 20.2. パイプライン演算はIdentity functorで関数合成（Function composition）ができる特別なFunctor モナド（Monad） 20.3. mapFunctorの連結の様子 Functorの合成（composition） 20.4. mapFunctorの合成（Functor composition）の問題点 20.5. flatMapMonadの登場 　 20.6. mapとflatMapの比較 20.7. flatMapは結合性と単位元があるFunctorなのでMonad 20.8. Monadの左右の単位元（Identity）はタイプコンストラクタ関数 20.9. Monadをもっと厳密にTypeScriptで定義していく 20.10. Monadの実装にはflatという概念が使われている 20.11. MonadはFunctorのより安全な上位互換となる代数構造 20.12. Monadのつくりかた 21. 「非同期（Asynchronous）」と命令型プログラミングという技術的負債とasync/await 21.1. ノイマン型コンピュータ 21.2. 現代ではノイマン型の命令型思考は技術的負債となっている 21.3. 「非同期（Asynchronous）」という用語 21.4. JavaScriptの非同期関数（Async function）async/await 22. 関数型リアクティブプログラミング（FRP） 時間に依存する関数型コードの書き方 22.1. 命令型コードは時間とコードの配置場所に暗黙に依存している 22.2. 命令型コードで普通にやっている値の書き換えというのは一体なんなのか？ ミュータブル（mutable）な世界 22.3. イミュータブル（Immutable）な世界 22.4. GitはImmutableな永続データ構造（Persistent data structure） 22.5. 関数そして二項演算子は暗黙に時間依存してはならない 22.6. 関数そして二項演算子が時間依存するときは明示的に依存グラフを構成する 22.7. 時間軸上のイベントを参照する関数 22.8. イベント駆動型プログラミング（Event-driven programming） 22.9. リアクティブプログラミング（Reactive programming） 22.10. PromiseはJavaScriptに導入された時間軸上のイベントのFunctor 23. シンプルでミニマルかつ強力なFRPの実装 23.1. Demo 23.2. ReactiveFunctor ReactiveMonad 23.3. ReactiveFunctor を実装するための下敷きとなるアイデア 23.4. ReactiveFunctor を実装するスタート地点 23.5. ReactiveFunctor のタイプコンストラクタ（型構築子） 23.6. ReactiveFunctor の二項演算子を表すreactive関数① 23.7. ReactiveFunctor のトリガー関数 change() 23.8. ReactiveFunctor の二項演算子を表すreactive関数② 23.9. 初歩的なReactiveFunctor のコード 23.10. 初歩的なReactiveFunctor のテスト 24. より安全なReactiveFunctor version2 24.1. やはりReactive値を保持する必要があった 24.2. ReactiveFunctor version 2 24.3. タイプコンストラクタ 24.4. reactive関数 24.5. change関数 24.6. version2のテスト 25. ReactiveFunctor version3 (typed with None) 25.1. Noneの導入 25.2. 型（Type）の導入 25.3. reactive演算子の追加　 25.4. タイプコンストラクタ 25.5. isNoneとoptionMap 25.6. version3のテスト 26. ReactiveMonad 26.1. flat機構の追加 26.2. flatReactive関数と演算子の追加　 26.3. タイプコンストラクタ 26.4. ReactiveMonad 結合性（Associativity）テスト 26.5. ReactiveMonad 左右の単位元（left & right Identity）テスト 26.6. ReactiveMonad ES Modules（ESM） 27. ReactiveMonadのエクステンション関数 27.1. Demo 27.2. ReactiveMonadとエクステンション関数の関係 27.3. エクステンション関数の実装 28. ReactのためのFRP（ReactiveMonad）のDemo その他 29. MIT License 30. フリー／購入 31. Contact　インスタフォロー/DM　シェアコメント　 1. 何が問題なのだろう？

バグがなく生産効率が高くメンテナンスが容易なプログラミングを実現したいのだが結構難しい

フォン・ノイマン型コンピュータというマシンを操作するという発想の命令型あるいはオブジェクト指向のプログラミングは、設計とコードが複雑になるから

マシンの状態を操作するという発想から脱却し、数学的手法に基づくシンプルで堅牢な関数型プログラミングの習得と実践

！！！！！

そして、なにより習得するための良い入門書がほぼほぼ存在していない、ことです。本稿は筆者が「もっと早く読みたかった」と2022年現在に考える関数型プログラミングの入門書です。 TypeScriptの知識と実践は推奨されますが、本書で読み進めるにあたって必須ではありません。むしろ多くの基本的な概念については、型（Type）は必要ではなく逆に煩雑になることが多いので、JavaScriptを優先しています。 2. 命令型プログラミング＝ほぼすべてのプログラミング入門者が半ば強制的に辿る道2.1. Start from Scratch（ゼロからのスタート）命令型プログラミング（Imperative Programming）は、コンピュータと呼ばれる物理的なハードウェアに順番に命令を送るという一連のシークエンスをコードとして並べる作業のことで、命令を送ればそのとおりマシンは動作するのだろう、という極めて自然で直感的にも理解しやすく原始的なやり方です。 2020年現在、ほぼすべてのプログラミング入門者は、まず命令型プログラミングの作法（プログラミングパラダイム (programming paradigm)）を徹底的に叩き込まれることからはじめる慣習になっています。

https://www.nhk.or.jp/school/programming/start/index.html これは、古典的で素朴なプログラミングの作法を学ぶという意味では正しいかもしれません。そして将来的にこの状況が改革されるのかどうかも良くわかりません。 命令型プログラミングのコードとは以下のようなものです。 1から10までの数を足すコード

ここで、たとえば

x = x + 1

というコードがありますが、実際には3つの操作を表現しています。 1. Xに割り当てられているメモリに格納された値を読み取る2. その値をひとつ増やす3. 新しい値を X に割り当てられているメモリに書き込む こういうメモリのに格納された「今」の値をプログラマは常に想像しながらコーディングしていくわけです。 http://www.f.waseda.jp/moriya/PUBLIC_HTML/social/Scratch/21.pdf とたいへん丁寧に説明されているわけですが、詳細がわかればわかるほど、命令型プログラミングのコードはかなり複雑なことをやっていることがわかってきます。 2.2. 命令型コード(JavaScript)

let sum = 0;let x = 0; for (let i = 0; i < 10; i++) { x = x + 1; console.log(x); sum = sum + x;} console.log(sum);

1234567891055 // sum

10回繰り返すループを作るためにforステートメントに i というカウンター変数を使うパターンです。 sum と x が繰り返しループとともに刻々と値が変化していき、コードの字面の変数名を見ただけでは、その値が何なのかは？頭のなかでコードのコンピュータの振る舞いをエミュレーションしなければならず、その途中で不等式　x ⩽10　なども判断していく、ということになります。 あるいはカウンターとして1ずつ増えていく変数ｉをｘの代わりに使うパターンもありえて、その場合は使う変数はひとつ減らせる！と考えられるのかもしれません。 しかし、実はこれは与えられた課題の本質とは全く関係ないコードの流れ自体をあれこれ考えなければいけないという別の問題に頭を酷使しているのです。 for 文 命令型プログラミングのコードはたいへん複雑なのです。 2.3. 命令型プログラミングに傾倒している「歪な状況」を根本的に解決する必要がある この根本的な問題を根本的に解決する必要があるのですが、ほぼすべての人は最初に刷り込まれたプログラミングの作法が命令型プログラミングなので、この命令型の作法こそがプログラミングの作法として至極当然であるとし、ここの部分のメンタルブロックが強烈で、なかなか発想を転換することができません。 そしてこれは何もプログラミングの経験が浅い初心者を中心に起こっていることではありません。実際には、後述するとおり、JavaScriptの仕様策定をしているグループであるTC39

の参加者でさえ、この命令型プログラミングへ過剰なまでに執着している現状があって、その結果、元来が本稿で解説するところである関数型プログラミングの概念の機能ですら、JavaScriptの新機能の仕様としては、命令型プログラミングの作法で実装されようとしている、というビックリ仰天のかなり歪な状態を筆者自身が目撃しており現状はかなり深刻であると感じています。 またこの種の問題点を共有しながら適切に解説しているドキュメントは非常に少なく、適切に発想を転換する機会に恵まれないことが現状です。本稿はその問題を適切にアプローチして解説することを目的としています。 3. 関数型プログラミング（Functional Programming）は式（Expression）の組み立て3.1. 関数型コード(JavaScript)上の命令型コードを関数型で書き直すならば、こうなります。

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add); console.log(sum);

55 // sum

課題の本質ではない無用な変数は取り除かれ、プログラマーの頭を悩ますループの流れも存在せず、ただ２つの式がconstによって宣言されているだけです。 このコードについては、今後複数章にまたがって詳しく解説していきます。3.2. 関数型コードは式（Expression）であるJavaScriptは、文（Statement）と式（Expression）から構成されています。 文と式(JavaScript Primer) 命令型プログラミングのコードは文（Statement）が中心でした。たとえば、for文 関数型プログラミングのコードは、それに対して、式（Expression）が中心です。 3.3. 関数型プログラミングは式（Expression）を組み立てていく作業 言い換えると、関数型プログラミングは式（Expression）を組み立てていく作業に他なりません。この作業は、命令型プログラミングの作業における、文（Statement）を組み立て、カウンター変数を別途に用意することも含めて刻々と変化する変数を監理しながら流れを整える、という作業とは根本的に異なります。 3.4. 関数型コードは値が変化するようなことはないlet で定義した i x sum のようにコードの流れで値がコロコロと変化していくようなことはなく、 const で定義するように値は定数として（一発で）定義されます。あとから値を二重に破壊的代入しようとするとエラーが出ます。

const x = 5;x = 10; // error

命令型では、

let x;x = 5;x = 10;

というコードがJavaScriptでもちろん有効で、実際、

for (let i = 0; i < 10; i++) {//....

というように命令型コードのforループを回すときなどに必要になってくるのですが、関数型コードではアンチパターンです。理由はコードの位置、上下関係で値が変化するので式自体に明示されていない余剰の要素が紛れ込んで論理構成が破綻するからです。これについては後々詳細に説明していきます、 関数型コードでは命令型コードのように命令文の上下の並びから発生するコードの流れ（フロー）をベースにするのではなく、式の構成によってプログラミングしていきます。 従って命令型のようにコードの振る舞いをコンピュータに成り代わってプログラマーの頭の中でのエミュレーションをしながら、あるいはデバッガーに利用して値の変化を追跡する必要がありません。与えられた課題の本質とは全く関係ないコードの流れ自体をあれこれ考えなければいけないという別の問題に頭を酷使する必要は消滅します。これは少なくともこのレベルではデバッグが不要である、ということを意味します。 そしてこの式（Expression）の中心となる素材が、関数と二項演算子です。 4. 関数と二項演算子　関数型コードの式を構成する主要部品4.1. 関数（Function）と二項演算子（Binary operator） 関数（Function）については数学的にも関数型プログラミングとしても、両方の観点で非常に重要で根幹となる要素だけに、後の章で改めて詳しく説明しますが、いきなり最初から数学全開でいくと解説としてとっつきにくい懸念があるので、今回はとりあえずなんとなくわかっているものとして取り扱います。 二項演算子（Binary operator）は、我々が小学１年かそれ以前から慣れ親しんでいる 1 + 2 というような２つの項目をあわせて一つにする演算（オペレーション）を 二項演算（Binary operattion）と呼び、そのうち• + は演算子(Operator)、あるいは英語カタカナ読みでオペレータ• 1,2,3などは被演算子(Operand) あるいは英語カタカナ読みでオペランドと呼びます。 ややこしく感じかねないですが、演算（Operation）は演算子(Operator)被演算子（Operand）というペア要素で構成されている、ということです。これは用語はともかくとして、わざわざ説明されずとも我々が小学校以来、直感的に理解している事実です。 1 + 2 というような二項の間の演算なら二項演算で＋は二項演算子だ、となるわけですが、 論理否定の演算子 !

!true // false!false // true

のように、一項演算子、または単項演算子というものも普通に存在しています。 4.2. 関数（Function）と演算子（Operator）は本当は同じものであるちょうど、一項演算子（単項演算子）の話が出たので、関数（Function）と演算子（Operator）の関係について、ここですぐ整理してしまいたいと思います。 関数（Function）と演算子（Operator）は本当は同じものです。 • 単項演算（Unary operation） の場合

単項演算とは、数学で、被作用子（オペランド）が一つだけであるような演算（つまり、入力が一つの演算）のこと。たとえば、論理否定は真理値に対する単項演算であり、自乗は実数に対する単項演算である。階乗 n! も単項演算である。与えられた集合 S に対する単項演算は、関数 S→S に他ならない。

たとえば、論理否定の演算子 !

!true // false!false // true

は、

const f = a => !a; f(true); // falsef(false); // true

と関数表記へそのまま置き換えることができ、一項演算子は１引数の関数(Unary function)と対応するのがわかります。

!(true) // falsef(true) // false

とすれば、単にシンボルの割当ての違いにすぎない、とはっきりとわかります。 • 二項演算（Binary operattion） の場合

これは図の通り、二項演算（Binary operattion）x ◦ y とは2引数の関数＝二項関数（Binary function）ｆ(x, y) であるということです。 つまり、１＋２という二項演算は、+(1, 2)という二項関数の糖衣構文（syntax sugar）にすぎない、ということです。 我々が小学校１年生の頃から扱って慣れ親しんでいた二項演算とは、中学に進級して初めて習う関数というものと正体は同じもので、関数のほうが概念としては統一的に全体を俯瞰することができます。 実際に、純粋関数型言語であるHaskellではこの事実に準じて実際に、二項演算子と関数表記の相互入れ替えが言語仕様として可能になっています。 中置と前置の切り替え ここでは、二項演算子はオペランドの間に挟まる記法なので、中置演算子と書かれていますね。 JavaScriptも同じように出来れば良いな、とは思いますし出来ないわけがないですが、今のところ意識が低いので出来ていません。JavaScriptの仕様策定団体であるTC39はJavaScript関数型プログラミングコミュニティの意に反して非常に意識が低いのは間違いありません。ただし、稀に良いことはあって、 べき乗 (**)という二項演算子がES2016で導入されました。

Math.pow(2, 3) ==2 ** 3 Math.pow(Math.pow(2, 3), 5) == 2 ** 3 ** 5

これは、まさに、二項関数（Binary function）Math.pow(x, y)を二項演算（Binary operattion）x ** yへ置き換えたものです。 4.3. 二項演算子（Binary operator）はとてつもなく強力な記法である まったく同じ意味のコードであっても、べき乗 (**)という新しい二項演算子を導入した結果、いかにコードが無駄なく簡潔になり、数学的な構造が読みやすくなったのかは明白です。 特にこのように連鎖してネスト構造になった場合、非常にシンプルに記述できます。これはバグの混入を事前に防ぐことができ、プログラミングの生産効率が飛躍的に向上することに直結します。 二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y) のことであり、概念としては、関数だけで統合できてしまうのですが、数式の表記方法としてはむしろ、x ◦ y のほうが圧倒的に優れており、なにより、これは繰り返しになりますが我々が小学校の算数の時間から徹底的にトレーニングされてきた慣れ親しんでいる表記でもあります。非常に直感的に理解可能です。 ”関数”型プログラミングとして、二項演算子という主要部品も根源的には関数という概念に統合される、という概念の統一感があります。それと同時に、関数型プログラミングで、実際にコードを書いていくのは、あくまで二項演算子を極限まで活用する、二項演算を主とする式（Expression）の組み立てとする、ということを本稿の一貫した理念とします。 実際にこの二項演算で式を組み立てて行く、という理念あるいは手法は、Haskellのような純粋関数型言語では、ほぼ自動的に達成されてしまうので、実際にHaskellのコードでは二項演算の式だらけで、非常に短いコードで高度なことを成し遂げているのだけれども、外部の人間からしてみると何をやっているのかよくわからない、ということが起こるでしょう。 JavaScriptの関数型プログラミングにおいて、この二項演算子を極限まで活用する、という理念あるいは手法は、あまり広くシェアされているとは観察されませんが、本稿を読みすすめるにつれて、その強力さは共有されていくと考えます。 5. オブジェクト指向のメソッドを関数型の二項演算子として置き換える5.1. 関数型＆オブジェクト指向のハイブリッド言語としてのJavaScriptJavaScriptは関数型プログラマーであるブレンダン・アイク（Brendan Eich）によって生み出されました。本人ブログエントリによると、実際に彼はNetScapeから、Webブラウザ実装言語にSchemeというLisp系の関数型言語を実装するという約束で雇用されたのですが、その過程で、Javaとオブジェクト指向ブームが巻き起こり、煽りを受けた結果、企業のマーケティングの理由から上層部の指示によって、「Javaのように見える」オブジェクト指向の性格をもつプログラミング言語が要求されることとなりました。その結果、世に送り出されたのが、関数型言語とオブジェクト指向の両方の性質を併せ持つハイブリッド言語としてのJavaScriptです。　オブジェクト指向自体をどのように定義するのか、ということ自体が歴史的に右往曲折があって厄介な問題なのですが、とりあえず巷で言われているオブジェクト指向プログラミング、言語では、たとえばC++やJavaは、関数型プログラミングを想定した代物ではありえない、という一点において原理的に命令型プログラミングを踏襲するカテゴリに入ると考えてまったく問題ありません。 関数型プログラミングをある程度以上のレベルで習得してしまうと、原理的にはオブジェクト指向プログラミングは不要の(冗長な)手法となります。関数型プログラミングは、オブジェクト指向プログラミングを完全に置き換えます。 なぜならば、関数型プログラミングは、すでに数学世界に存在している式（数式）を組み立てる、という極めてシンプルで解釈のブレのない作業ですが、オブジェクト指向プログラミングは同じ作業をオブジェクトという本質的には必要はなかった（あまり出来の良くはない）人工的に発明された枠組みの中で、様々な複雑なルールをそのオブジェクトに付与した冗長なフォーマットに焼き直した上で、こういうデザインパターンが望ましい、アンチパターンだ、と設計の欠点の辻褄あわせをしているにすぎないからです。 5.2. オブジェクト指向時代の終焉 当時の熱狂的なオブジェクト指向ブームは2020年代においてはとっくに過ぎ去り、長期に渡る壮大な検証実験を経た結果、多くの問題が指摘されるようになってきました。関数型プログラミングと比較してオブジェクト指向批判の数々の記事がWeb検索でヒットします。日本語の良記事も多くありますし、やはり英語圏のものも多いのでGoogle翻訳などをして読むと良いかもしれません。 Object-Oriented Programming — The Trillion Dollar Disasterオブジェクト指向言語ーそれは何兆ドル規模の厄災 さらに、JavaScriptが必須であるWebのフロントエンド界隈では、壮大な実験が行われました。Reactです。

JavaScriptはES2015(ES6)時代になり、オブジェクト指向そのもののClass（クラス）が新たに導入されました。これに伴い、Reactでも、フレームワークの根幹となるコンポーネントをClassで表現するように標準化されました。 筆者などは「いくらJavaScriptが根強いオブジェクト指向ファンの要請から、後方互換性のようなクラスが導入されたからといって、Reactのようなメジャーな外部ライブラリまでそれに習うのは困ったことになった、時代の逆行だ」と、まったく歓迎していませんでした。案の定、オブジェクト指向のクラスを標準コンポーネントとして利用するというReactのアプローチは失敗し、実質クラス実装のコンポーネントは破棄し、関数型に近いHooksという仕組みが導入されることになりました。 以下はIntroducing Hooksからの引用です。

Classes confuse both people and machinesIn addition to making code reuse and code organization more difficult, we’ve found that classes can be a large barrier to learning React. You have to understand how this works in JavaScript, which is very different from how it works in most languages. You have to remember to bind the event handlers. Without unstable syntax proposals, the code is very verbose. People can understand props, state, and top-down data flow perfectly well but still struggle with classes. The distinction between function and class components in React and when to use each one leads to disagreements even between experienced React developers. クラスは人も機械も混乱させるコードの再利用やコードの整理が難しくなるだけでなく、クラスがReactを学ぶ上で大きな障壁になることがわかりました。これがJavaScriptでどのように動作するかを理解しなければならず、それはほとんどの言語で動作する方法とは大きく異なります。イベントハンドラをバインドすることを覚えなければなりません。不安定な構文の提案がなければ、コードは非常に冗長になります。人々は、プロップ、ステート、トップダウンのデータフローは完璧に理解できても、クラスには苦労します。Reactにおける関数コンポーネントとクラスコンポーネントの区別と、それぞれをいつ使用するかについては、経験豊富なReact開発者の間でも意見の相違が見られます。

To solve these problems, Hooks let you use more of React’s features without classes. Conceptually, React components have always been closer to functions. Hooks embrace functions, but without sacrificing the practical spirit of React. Hooks provide access to imperative escape hatches and don’t require you to learn complex functional or reactive programming techniques. これらの問題を解決するために、HooksはクラスなしでReactの機能をより多く使用できるようにします。概念的には、Reactのコンポーネントは常に関数に近いものでした。Hooksは関数を受け入れますが、Reactの実用的な精神を犠牲にすることはありません。Hooksは、命令的なエスケープハッチへのアクセスを提供し、複雑な関数型またはリアクティブプログラミング技術を学ぶ必要はありません。

オブジェクト指向については、おもにオブジェクト指向の習得に長い時間を費やしたオブジェクト指向ブームに生きたプログラマーによって強い擁護がなされてきたのですが、結局の所、われわれプログラマーコミュニティはエンジニアであり現実世界でその技術がうまく機能するかどうか？というのは生命線といえるものであり、実際にReactのような大規模なシェアをもつWebフレームワークでうまく行かなかった、という厳然たる事実は到底覆い隠されるものではありませんでした。 結果「より関数型的」なReactHooksが導入されたわけですが、

Hooksは関数を受け入れますが、Reactの実用的な精神を犠牲にすることはありません。Hooksは、命令的なエスケープハッチへのアクセスを提供し、複雑な関数型またはリアクティブプログラミング技術を学ぶ必要はありません。

とあるのは、ここも根源的な間違いを犯しており、ReactHooksはかなり複雑で習得コストが高く、筆者個人はまったく評価していません。実際に読者でも使いづらいと理解している人たちはきっと多いでしょうし、実際に品質に不満な第三者がさまざまなより本質的に関数型的なアプローチのサードパーティの代替物がリリースされています。 5.3. オブジェクト指向のメソッドと二項演算の関係とはいえ、JavaScriptはオブジェクト指向言語でもあり、オブジェクト指向は言語の根深い実装と直結しており、オブジェクトとメソッドという構造が言語の基本となっています。関数型プログラミングをこれから志向していこうとしても、絶対に避けられるものではありません。 では、JavaScriptにおいて切り離すことができないオブジェクト指向の表記は、関数型プログラミングで扱う式としてどのように解釈すべきでしょうか？ JavaScriptはオブジェクト指向言語でもあり、オブジェクトとメソッドという構造が言語の基本となっています。 たとえば文字列はStringオブジェクトという構造で定義されていて、String.concat() というメソッドがあらかじめ実装されています。

concat() メソッドは、文字列引数を呼び出し文字列に連結して、新しい文字列を返します。

"Hello".concat("World") // "HelloWorld""Hello".concat(" ").concat("world!") // "Hello world!"

「へーStringオブジェクトにこんなconcatというオブジェクトがあるのか！初めて知った」という読者もいることでしょう。なぜならば我々はこんなオブジェクトメソッドのまわりくどい表記は無視して、シンプルにこう書くことを好むからですね。

"Hello" + "World" // "HelloWorld""Hello" + " " + "world!" // "Hello world!"

まったく同じ意味と動作のコードなのですが、どちらが書きやすく、読みやすく、デバッグもしやすいのかは一目瞭然です。 String.concat(String) = Stringというオブジェクト指向のコードがString + String = Stringという二項演算に置き換えられる、という事実から以下の事実が明らかになります。 オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数（Parameter）は、二項演算の右側の被演算子（Operand）になります。 また、オブジェクトのメソッドチェーンは、二項演算の連鎖と同じものである、という事実をかんたんなJavaScriptのコードから認識できるでしょう。

"Hello" .concat(" ") .concat("world!") "Hello" + " " + "world!"

二項演算子（Binary operator）はオブジェクト指向のコードを置き換え可能な、強力な表記法です。 また、JavaScriptの配列データ構造を司るArrayオブジェクトにはArray.concat() というメソッドがあらかじめ実装されています。String.concat()とまったく同じメソッド名であることに注目してください。

concat() メソッドは、2つ以上の配列を結合するために使用します。このメソッドは既存の配列を変更せず、新しい配列を返します。 const array1 = ["a", "b", "c"];const array2 = ["d", "e", "f"];const array3 = array1.concat(array2); // ["a", "b", "c", "d", "e", "f"]

同じメソッド名で、機能面でもまったく同じ概念であることが確認できます。 JavaScriptでは、文字列の結合（連結）のための二項演算子が加法演算子のシンボルである + を共有していることを考えると、

"Hello" + "World"; // "HelloWorld"

配列の結合（連結）のための二項演算子も、同じように加法のシンボルである + を共有していても別に問題なかったはずです。

["a", "b", "c"] + ["d", "e", "f"]; // ["a", "b", "c", "d", "e", "f"]

こんなふうに。しかしこれは "a,b,cd,e,f" という変な結果になります。TypeScriptなら未然にちゃんとエラーが出ます。

文字列構造であるStringsと配列データ構造であるArrayは異なるオブジェクトですが、同じ機能を目的とする同じメソッド名のconcatを共有しています。しかし前者では便利に直感的に二項演算子 + を使えていたのに、後者では使えません。 実は、ここには別段合理的な理由など存在せず、ただ単にJavaScript言語実装の気まぐれにすぎないのです。べき乗の二項演算子をES2016で新規導入したのと同じように今からでも新規実装できるような事案ではあるのでしょう。 なんとかならないでしょうか？ 5.4. JavaScriptで独自の二項演算子（Custom operator）を定義するJavaScriptでは現在このような機能はありません。tc39/proposal-operator-overloadingという既存の演算子のオーバーロードの検討はあるにはありますが、まったく活発ではないようですし、残念ながらTC39にはあまり期待できません。 しかし、多少のハック的手法を許容するのであれば、なんとかはなります。それが本書の手法です。すべては二項演算子を活用するという根幹の目的を達成するためです。逆にこの最難関ポイントを突破することさえできれば、関数型プログラミングの見通しがクリアになり、視野は広がり、理解を深めることが容易になります。 では、はじめてみましょう。 シンプルなお馴染みの + という二項演算子を用いた、加法の二項演算 1 + 2 = 31 + 2 + 3 = 6 は、＋という二項演算子によって、JavaScriptのオブジェクトとしてNumberとNumberいう集合同士からNumberが演算される、と代数的に定義されています。 これは、オブジェクト指向の世界に翻訳すると、Numberオブジェクトに＋(Number)というメソッドが実装されていてNumberを返すということと同じです。つまり、

Object.defineProperty( Number.prototype, "plus", { value: function (R) { // R is Right hand side or the Binary operator return this + R; // `this` is Left hand side of the Binary operator }});

と、Numberオブジェクトにplusメソッドを拡張してやることで、

(1).plus(2); // 3(1).plus(2).plus(3); // 6

とオブジェクト指向の表記で記述することも可能です。 さらに、plusではなく本当に + という記号で拡張定義することも可能です。

Object.defineProperty( Number.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this + R; // `this` is Left hand side of the Binary operator }});

この場合は、オブジェクト指向的な . (ドット)記法ではSyntaxErrorになるので、代わりにプロパティ/連想配列形式でうまく書けます。

(1)['+'](2); // 3(1)['+'](2)['+'](3); // 6

と車輪の再発明をすることも可能です。 同様に、Arrayオブジェクト に+ という記号のプロパティでArray.concat() というメソッドを拡張してしまいます。

Object.defineProperty( Array.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this.concat(R); // `this` is Left hand side of the Binary operator }});

このコードでは、this.concat(R) と単純にArrayオブジェクトメソッドを + というオブジェクトプロパティにコピーしています。その結果、

array1.concat(array2);array1['+'](array2);

となります。

["a", "b", "c"] + ["d", "e", "f"]; // ["a", "b", "c", "d", "e", "f"]

と書くのは言語仕様的に無理でも、

["a", "b", "c"]['+'](["d", "e", "f"]); // ["a", "b", "c", "d", "e", "f"]

と書くことは可能になりました。 JavaScriptで独自の二項演算子（Custom operator）を定義することに成功しました。 Object.defineProperty()では、デフォルトの設定では、プロパティの値は変更することはできず、プロパティ列挙可能性がfalseになります。プロパティの列挙可能性と所有権

列挙可能プロパティは、内部の列挙可能enumerableフラグが true に設定されているプロパティです。これは、単純な代入や初期化で作成されたプロパティのデフォルトです (Object.defineProperty で追加したプロパティはデフォルトで列挙可能性が false になります）。

5.5. 既存のオブジェクトメソッドを二項演算子として捉え直す上記のとおり、オブジェクトメソッド表記が、オブジェクトプロパティ/連想配列形式で表記できる、というのは、逆方向に応用することも可能です。つまり、

array1.concat(array2);array1['concat'](array2);

と書き直せるということで、すでに確認したとおり、

オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数（Parameter）は、二項演算の右側の被演算子（Operand）になります。

という事実が、オブジェクトメソッド表記から一旦離れることにより、意識しやすくなります。もちろん、既にオブジェクトメソッド表記で簡潔に書けていることは間違いないので、無理に書き直す必要性はないでしょうが、あくまで二項演算子として扱うことを常に意識するためには役立つでしょう。 同様の原理で、Arrayオブジェクトには最初から.mapメソッドが実装されていることを考慮して、

const f = a => a + 1; [1, 2, 3].map(f); // [2, 3, 4][1, 2, 3]['map'](f); // [2, 3, 4]

というように、Array.map(f) メソッドというのは、配列Arrayと関数f との間の二項演算子 map である、と理解できます。 では、ここで課題である関数型のコードを見てみましょう。

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add);

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add)

という、オブジェクト指向フォーマットで書かれた式は、

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]['reduce'](add)

と二項演算であることを強く意識したフォーマットへ書き直すこともできて、 reduce は、 • 配列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] • 関数 add の間の二項演算を司る二項演算子であると代数的に理解できます。（代数学についてはあとで説明） まとめると、 • 加算演算子である + は、NumberとNumberからNumberを生み出す二項演算子です。• Number + Number = Number• 1 + 2 = 3 • 文字列結合としての + は、とStringとStringからStringを生み出す二項演算子です。• String + String = String• "Helllo" + "World!" = "HelloWorld!"• • 配列結合としての 'concat' は、ArrayとArrayからArrayを生み出す二項演算子です。• Array 'concat' Array = Array• [1,2,3] ['concat'] ([4,5,6)] = [1, 2, 3, 4, 5, 6] • 'map' は、ArrayとFuncttionからArrayを生み出す二項演算子です。• Array 'map' Function = Array• [1,2,3] ['map'] (f) = [2,3,4] • 'reduce' は、ArrayとFuncttionからObjectを生み出す二項演算子です。• Array 'reduce' Function = Object• Object はFunctionの働きによって変わる。• [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ['reduce'] (add) = 55 二項演算子 'reduce' についてはまだまだ謎につつまれているので、さらなる探求が続く章とともに必要です。 6. 式の組み立ては依存グラフの構成6.1. もっとも単純な関数型コードJavaScriptは、文（Statement）と式（Expression）から構成されている。命令型プログラミングのコードは、forループなどの文（Statement）が中心、関数型プログラミングのコードは、それに対して、式（Expression）が中心。 関数型コードは式（Expression）である。関数型プログラミングは式を組み立てていく作業。 式の中心となる素材が、関数（Function）と二項演算子（Binary operator）。 関数（Function）と演算子（Operator）は本当は同じものである。二項演算子（Binary operator）はとてつもなく強力な記法である。 これが一番の大枠のまとめです。この大枠に付随する、どうしても説明しておかなければならなかった事柄も説明出来たと思います。 では実際に、式を組み立てていくとして、もっとも単純なコードは何でしょうか？ おそらくもっとも単純な式とは、

1

あるいは

"hello"

こんな感じでしょう。これがもっとも単純な関数型のコードです。 ではもう少し進んで、

1 + 2

より関数型コードらしくなりました。なぜならば、関数（Function）と演算子（Operator）は本当は同じもの二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y)

であることはすでに確認済みなので、1 + 2 は実際に関数（Function）を扱う式（Expression）である関数型コードです。よく考えると、我々は全員、小学校の義務教育の範囲内ですでに関数型コードを書いていた、ということになります。 6.2. 少し複雑な関数型コードさらにもう少し複雑にしてみましょう。

1 + 2　+ 3

この関数型コードは、数学の＋演算子のルールによって、実際には暗黙の了解で、

(1 + 2)　+ 3

と解釈されます。数学であってもJavaScriptコードであっても変わりはありません。 というより、関数型プログラミングの力の源泉は数式であり数学そのものであるので、もし「プログラミングと数学は違う」であるとか「JavaScriptは純粋関数型言語ではないし関数型プログラミングは無理だ」という愚言が呈された場合は、それはたいてい強い命令型プログラミングへの傾倒によるメンタルブロックによるものですし、「このコードの振る舞いは数学とは異なる」と示された場合、本当にそうなのか慎重に吟味する必要がありますし、もし本当にそれが数学の振る舞いと異なるJavaScriptパーツなのであれば、関数型コードを書く場合は重大な障害になりうると認識し回避策を熟慮したほうが良いです。 JavaScriptのグループ化演算子 ( ) は、式における演算の優先順位を制御します。これは数学の（）の振る舞いと等価です。 このとき、式の構造は

このように構成されました。上のコードと対比させると、x=1, y=2, z=3 です念の為。 6.3. 依存グラフ（Dependency graph）を構成する式（関数型コード）を書いてコンピュータに解決してもらう 上記の図はグラフを構成しています。特に依存（関係）グラフ（Dependency graph）などと呼ばれているものです。

In mathematics, computer science and digital electronics, a dependency graph is a directed graph representing dependencies of several objects towards each other. It is possible to derive an evaluation order or the absence of an evaluation order that respects the given dependencies from the dependency graph. 数学やコンピュータサイエンス、デジタルエレクトロニクスの分野で、依存（関係）グラフは、複数のオブジェクトの相互依存関係を表す有向グラフ （directed graph）である。依存関係グラフから、与えられた依存関係を尊重した評価順序や評価順序がないことを導き出すことができる。

依存関係グラフから、与えられた依存関係を尊重した評価順序や評価順序がないことを導き出すことができる。

とあるとおり、関数型のコードでは、演算子とともにグループ化演算子 ( ) を組み合わせることで依存グラフを構成し、演算はその依存グラフを解決する形で進んでいきます。 これは数学とほぼ全てのプログラミング言語において共通の仕様です。「ほぼ全て」と留保したのは、別に作ろうと思えば一般的な数学規則としての（）の規則を無視したプログラミング言語を設計することはいくらだって可能だからです。しかしメジャーな言語たとえば、CやJava、JavaScript、Haskell、Pythonでは、このグループ化演算子（）の振る舞いは同一でしょう。

1 + 2　+ 3 + 4 + 5

あるいは演算ルールに則って暗黙に省略されてしまっているグループ化演算子 ( ) を明示して

((((1 + 2)　+ 3) + 4) + 5)

という式＝関数型コードについて

依存関係の矢印の向きの解釈を逆にして表現すると、さらに依存グラフらしく表現すると、こうなります。

プログラマーが関数型コードの式を組み立てていくときは、このように二項演算子と（）を活用して依存グラフを構成します。 JavaScriptの実行環境は、式（Expression）によって構成された依存グラフを解析し、解決していくことによってコードを実行していきます。 依存（関係）グラフはソフトウェア開発分野でありふれた概念で、パッケージマネージャーやあるいはGitHubレポジトリなどに見られます。 依存関係グラフについて

GitHubの依存関係グラフ~ 開発ワークフロー全体をセキュアに

オープンソースの利用が加速する中で、プロジェクトにはおそらく何百もの依存関係が存在します。平均でリポジトリあたり203個のパッケージ依存関係が存在することがわかっています。アプリケーションにどのような依存関係があるのか、どうすれば実際に判断することができるのでしょうか。ドキュメントまたはStack Overflowからコードを自分のコードにコピペしすることも、依存関係と言えるでしょう。 依存関係とは何か、また、GitHubの依存関係グラフでコードどのような影響があるかを確認する方法について、そして依存関係を安全に維持するために何をすべきかについて、詳しく見ていきましょう。 依存関係の把握依存関係はソフトウェアの実行に必要なバイナリです。これには、アプリケーション開発時に必要なバイナリ(多くの場合、開発依存関係と呼ばれる)と、実行時にアプリケーションの一部として実際に使用されるバイナリの両方が含まれていると考えることができます。また、スタックの他の部分にも依存関係があります。たとえば、アプリケーションがオペレーティングシステム上で実行される、などです。ただし、ここでは分かりやすくするために、これについては除外します。 依存関係は、開発者がアプリケーションの一部として指定したときに環境に取り込まれます。これは通常、依存関係が宣言されるマニフェストファイル、または特定バージョンの依存関係が指定されるロックファイルの一部として実行されます。依存関係は推移的に含まれる場合もあります。つまり、特定の依存関係を指定していなくても、自分で指定した依存関係によって指定されている場合、結果的にその依存関係に依存することになります。 これが、ネットワーク効果を介して依存関係が急速に拡大する仕組みであり、アプリケーションが何に依存しているかを識別することが難しくなる理由ともなります。これを簡単に把握できるようにする一般的な方法は、依存関係を非巡回グラフとして提示し、レビューすることです。つまり、あるバイナリから別のバイナリへの依存の方向を示すことによって、一連の依存関係を表示します。ファミリーツリーと同様に、アプリケーションには直接引き込む依存関係があり(ファミリーツリーにおけるペアレントのようなもの)、その依存関係にも独自の依存関係(ペアレント関係の上位のようなもの)があります。ただし、類似しているのはそこまでです。複数の項目がすべて1つのバイナリにつながる可能性があり、また所有する依存関係の数に制限はありません。おそらく、”ペアレント関係のさらに上位の関係”よりもさらに前に遡ることができます。

6.4. 計算不可能な巡回グラフ 有向閉路グラフ (directed cycle graph)

これが、ネットワーク効果を介して依存関係が急速に拡大する仕組みであり、アプリケーションが何に依存しているかを識別することが難しくなる理由ともなります。これを簡単に把握できるようにする一般的な方法は、依存関係を非巡回グラフとして提示し、レビューすることです。

とありますが、なぜ依存関係は、非巡回グラフというものなっているのでしょうか？ 非巡回グラフでないほうの巡回グラフというのはプログラミングでもあまり耳慣れない言葉ですが、プログラマーに限らず一般の人でも聞いたことのある言葉でいうならば要するに無限ループのことです。 グラフ理論では、有向閉路グラフ (directed cycle graph)などと呼びますが、別にここでは積極的にこの用語を覚える必要はありません。ただし、概念としては常識的に理解しておく必要はあるし、実際にこういうGitHubのドキュメントでも非巡回グラフであるとか、その下敷きとなる重要概念として紹介されていたりはするので、用語が出てきたら、ああアレのことか、とわかれば、プログラマとしてもかなりのアドバンテージにはなります。

有向閉路グラフ (英: directed cycle graph) は辺に向きのある閉路グラフであり、全ての辺は同じ向きになっている。閉路のない有向グラフは有向非巡回グラフ (英: directed acyclic graph) という。

これは計算可能性理論とも密接な関係があって、チューリングマシンの停止問題や、もっと一般的に循環論法と同じことである、というのは直感的にも理解できるのではないでしょうか？ 以下は、循環論法の概念図ですが、巡回グラフとまったく同じ概念であることは一目で理解できるでしょう。

無限ループ、循環論法は、巡回グラフ、有向閉路グラフ (directed cycle graph)であり、計算不可能です。 そしてこれが

依存関係グラフから、与えられた依存関係を尊重した評価順序や評価順序がないことを導き出すことができる。

のうち「評価順序がないことを導き出す」という依存関係グラフのケースです。 チューリングマシンの停止問題でも

アラン・チューリングは1936年、停止性問題を解くアルゴリズムは存在しないことをある種の対角線論法のようにして証明した。 すなわち、そのようなアルゴリズムを実行できるチューリングマシンの存在を仮定すると「自身が停止するならば無限ループに陥って停止せず、停止しないならば停止する」ような別の構成が可能ということになり、矛盾となる。

とあるように、原理的に、関数型コードであっても命令型であっても、有向閉路グラフ (directed cycle graph)は計算不可能であるので、プログラミングのコードとして成立しません。 6.5. 計算可能な有向非巡回グラフ（DAG）ただし、再帰（Recursion）あるいは、もっと一般的に、自己相似（Self-similarity）あるいは、フラクタル構造（Fractal）

もしくは、自己言及（Self-reference）https://plato.stanford.edu/entries/self-reference/

というのは、OSのディレクトリツリー構造としても普通に使われています。

あるディレクトリは別のディレクトリを含む再帰構造になっています。 循環論法 関連項目

再帰プログラミング形式的には、「ある用語の定義を与える表現の中にその用語自体が登場」しており、一見すると循環定義そのもののような構造で書かれているが、再帰で辿っていける鎖の端に具体的な値を決定できる要素が最低でもひとつ見つけられるように記述しておけば、プログラムとして立派に作動する。決定できる要素が与えられないと再帰プログラムとして成立せず、まともに動作しない。）

つまり、無限ループは計算不能になって使い物にならないが、有限ループのグラフ構造なら計算可能だし、それは、巡回グラフにはなっていない、ということです。 命令型プログラミングでは、フローの制御文のForやWhileをある種のステートメントのパターンとして繰り返し構造を表現しますが、関数型プログラミングでは、このように自然界や工学的な構造として普通に現れる、再帰（Recursion）構造を強く意識して、依存グラフとして構成し、式で表現します。 巡回グラフあるいは、有向閉路グラフ (directed cycle graph)になっていない、つまり、計算可能で無限ループになってないグラフのことは、有向非巡回グラフ（Directed acyclic graph）と呼びます。

有向非巡回グラフ、有向非循環グラフ、有向無閉路グラフ（ゆうこうひじゅんかいグラフ、英: Directed acyclic graph, DAG）とは、グラフ理論における閉路のない有向グラフのことである。有向グラフは頂点と有向辺（方向を示す矢印付きの辺）からなり、辺は頂点同士をつなぐが、ある頂点vから出発し、辺をたどり、頂点vに戻ってこないのが有向非巡回グラフである[1][2][3]。 有向非巡回グラフは様々な情報をモデル化するのに使われる。有向非巡回グラフにおける到達可能性は半順序を構成し、全ての有限半順序は到達可能性を利用し有向非巡回グラフで表現可能である。順序づけする必要があるタスクの集合は、あるタスクが他のタスクよりも前に行う必要があるという制約により、頂点をタスク、辺を制約条件で表現すると有向非巡回グラフで表現できる。トポロジカルソートを使うと、妥当な順序を手に入れることができる。加えて、有向非巡回グラフは一部が重なるシーケンスの集合を表現する際の空間効率の良い表現として利用できる。また、有向非巡回グラフはイベント間の因果関係を表現することにも使える。さらに、有向非巡回グラフはデータの流れが一定方向のネットワークを表現することにも使える。

有向非巡回グラフ（Directed acyclic graph, DAG）は、依存グラフ（Dependency graph）のなかで依存関係のサイクル（循環依存関係）が存在しない特殊なケースであり、関数型プログラミングあるいは本稿で、依存グラフというときには、有向非巡回グラフ（Directed acyclic graph）のことを意味します。原理的に計算可能なのはこちらでしかないからですね。

In a dependency graph, the cycles of dependencies (also called circular dependencies) lead to a situation in which no valid evaluation order exists, because none of the objects in the cycle may be evaluated first. If a dependency graph does not have any circular dependencies, it forms a directed acyclic graph, and an evaluation order may be found by topological sorting. 依存関係グラフにおいて、依存関係のサイクル（循環依存関係とも呼ばれる）は、サイクル内のどのオブジェクトも最初に評価することができないため、有効な評価順序が存在しないという状況を引き起こす。依存グラフに循環依存性がない場合、それは有向非巡回グラフ（DAG）を形成し、トポロジカルソートによって評価順序を見つけることができる。

有向非巡回グラフはイベント間の因果関係を表現することにも使える。

というのは、関数型プログラミングの文脈でいうと、関数型リアクティブプログラミング（FunctionalReactiveProgramming）つまりFRPのことです。 演算可能な式を二項演算子やグループ化演算子（）を活用して代数的に構成することは、有向非巡回グラフ（Directed acyclic graph, DAG）を構成することであり、これはそのままイベント間の因果関係を表現することが可能です。 実際、前述のReactHooksでも取り扱っている対象であるReactコンポーネントの状態管理には、このDAGを使うFRPの原理で実装すべきでしたが、少なくと理念としては、

Hooksは関数を受け入れますが、Reactの実用的な精神を犠牲にすることはありません。Hooksは、命令的なエスケープハッチへのアクセスを提供し、複雑な関数型またはリアクティブプログラミング技術を学ぶ必要はありません。

とFacebookの担当技術者自身が明言してしまっているのは非常に残念なことです。 FRPについては関数型プログラミングを実世界のアプリケーションで活用するために必須なので本稿の後半では詳細に説明します。 6.6. 命令型プログラミングのフローをコントロールする文（Statement）は完全に不要だった　数式でやれば良いJavaScriptの実行環境は、式（Expression）によって構成された依存グラフを解析し、解決していくことによってコードを実行する能力が数学の原理原則としてデフォルトで最初から装備されているのであれば、命令型プログラミングのフローをコントロールする文（Statement）別の言葉では、制御構造（Control flow）と呼ばれる仕組みってそもそも必要？？となりますよね。 命令型プログラミングのこれはいったいなんだったのか？

有向非巡回グラフ（Directed acyclic graph, DAG）の、依存グラフ（Dependency graph）を構築すれば良いのです。 実際はまだ我々は積み残した課題、あるいは謎が残っています。上の命令形フロー文を式に置き換えた関数型コード

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add);

あるいは、

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add)

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]['reduce'](add)

この二項演算子'reduce'の振る舞いの謎です。 6.7. 二項演算'reduce'の振る舞いの謎 都合上、長いので、このサンプルコードを

[1, 2, 3, 4, 5]['reduce'](add)

へ置き換えます。 • 'reduce' は、ArrayとFuncttionからObjectを生み出す二項演算子です。• Array 'reduce' Function = Object 'reduce'の二項演算の仕組みは、左側のオペランドとして与えられた配列集合（Array）[1, 2, 3, 4, 5]を素材として並び順に従い、右側のオペランドとして与えられた二項関数　add = (a, b) => a + b によって順次演算を行います。 つまり、

'reduce'とは、まさにこのとおりの依存グラフを構成する二項演算子だったのです。 これは日本語では畳み込み、英語ではfoldとして、広く知られています。

In functional programming, fold (also termed reduce, accumulate, aggregate, compress, or inject) refers to a family of higher-order functions that analyze a recursive data structure and through use of a given combining operation, recombine the results of recursively processing its constituent parts, building up a return value. Typically, a fold is presented with a combining function, a top node of a data structure, and possibly some default values to be used under certain conditions. The fold then proceeds to combine elements of the data structure's hierarchy, using the function in a systematic way. 関数型プログラミングにおいて、fold（reduce、accumulate、aggregate、compress、inventとも呼ばれる）とは、再帰的なデータ構造を分析し、与えられた結合操作を使用して、その構成部分を再帰的に処理した結果を再結合し、戻り値を構築する高階関数のファミリーを指します。通常、フォールドには、結合関数、データ構造のトップノード、および特定の条件で使用されるデフォルト値が提示されます。フォールドはその後、データ構造の階層の要素を結合し、関数を体系的に使用していきます。

つまり、Array.reduceあるいはFoldという関数は、

命令型プログラミングでは、フローの制御文のForやWhileをある種のステートメントのパターンとして繰り返し構造を表現しますが、関数型プログラミングでは、このように自然界や工学的な構造として普通に現れる、再帰（Recursion）構造を強く意識して、依存グラフとして構成し、式で表現します。

の具体例だったのです。 結合操作（combining operation）、高階関数（higher-order functions ）という用語については、かなり重要なので、これも独立した章で詳細に説明していきます。 6.8. 依存グラフを構成する二項演算を最大限に活用した式の組み立て命令型コード

let sum = 0;let x = 0; for (let i = 0; i < 10; i++) { x = x + 1; console.log(x); sum = sum + x;} console.log(sum);

は、関数型コードに数学の式として洗練された理念で置き換えが可能で、

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add)

あるいは

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]['reduce'](add)

という式を書くことは、

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10

という式を書くことと等価で、これらの式をもってまったく同じ依存グラフを構成している、ということになります。 このように、コントロールフローの文や変数を追跡しながら命令型コードを書くのではなく、依存グラフを構成する二項演算を最大限に活用した式の組み立てに注力することで、バグの入り込む余地が極小の関数型コードを書くことが実現できます。 7. 命令型コードのif文switch文は場合分けの演算式にする7.1. 命令型コードのif文 JavaScriptは、文（Statement）と式（Expression）から構成されている。命令型プログラミングのコードは、forループなどの文（Statement）が中心、関数型プログラミングのコードは、それに対して、式（Expression）が中心。 関数型コードは式である。関数型プログラミングは式を組み立てていく作業。式の組み立ては依存グラフの構成。JavaScriptの実行環境は、式（Expression）によって構成された依存グラフを解析し、解決していくことによってコードを実行。 式の中心となる素材が、関数と二項演算子。 関数（Function）と演算子（Operator）は本当は同じもの二項演算子はとてつもなく強力な記法 これが一番の大枠のまとめです。ここで、命令型プログラミングのコードは、forループなどの文（Statement）が中心、と、命令型のサンプルコードに即して書いたのですが、他に大事な制御文として、条件分岐を司るif文があります。

if 文は、指定された条件が truthy ならば文を実行します。条件が falsy なら、もう一方の文を実行することができます。

よく見るフローチャートの条件分岐ではこのようなダイアグラムのシンボルで表現されていることが多いです。

上の図はそっくり、電車の線路の分岐と同じ概念ですね。

ちょうど電車がレールにそって、分岐器（ポイント）で進行方向が変わる、というようなことであり、その分岐されたそれぞれの行き先には、それぞれの命令文が用意されており、それを実行することになる、と。 for文によるルーブの中にもこの条件分岐の概念、つまりループの流れから脱出するための条件文が含まれており、全く同じことなのですが、このような条件分岐の文を書き連ねることによりコードの流れをコントロールしようとする命令型コードの問題点は、プログラマーがいちいち「電車に乗って分岐の流れに沿って進む必要がある」ことです。頭のなかで電車に乗って、ここがポイントだからこっちに流されて行って、と簡単なときはなんとかなるでしょうが、コードがどんどん複雑になってくると、まったくなんとかならない方が多く、本当にこのポイントでこちらに流されているのだろうか？この現在自分が居る位置は本当に正しいのだろうか？というシミュレーションの正しさの検証が必要となり、それはBUGの温床になっています。 実際にブレークポイントとかバグトラッカーというのは、関数型プログラミングで利用局面はない、とは言えないまでも、ほぼほぼこういう命令型の分岐やループを含むコードの流れを確認するために利用されており、これはデバッグにおいて大変な負担です。 関数型コードではこのようなフローチャートの条件分岐の先に待機している「文（statment）を実行」という流れを制御するのではなく、あくまで式（expression）の組み立てをするだけなので、このようなif文は使いません。 7.2. 関数型コードのif式遠回りのようですが、一旦、JavaScriptではない関数型プログラミングの流れが強いRustでは、if文がどうなっているのか？と確認すると、ifは文ではなく、式になっています。 if/else（Rust By Example 日本語版） これは純粋関数型言語であるHaskellでも同様です。 7.3. 条件 (三項) 演算子をつかうJavaScriptには幸か不幸かif文をそのまま置き換えるif式というものが存在しないので、代わりに条件 (三項) 演算子を利用します。これは実質if式なのです。

条件 (三項) 演算子は JavaScript では唯一の、3 つのオペランドをとる演算子です。条件に続いて疑問符 (?)、そして条件が真値であった場合に実行する式、コロン (:) が続き、条件がfalsyであった場合に実行する式が最後に来ます。この演算子は、 if 文のショートカットとしてよく用いられます。

要するに場合分けをする演算子です。条件式があり、その結果、ある値が決定されます。 C言語の流れを汲むJavaScriptの条件 (三項) 演算子の書式は<条件式> ? <真式> : <偽式> 3項を結ぶ必要上、 (?)と (:) の2つの記号を使うが、演算子としては1つの演算子。 １つの演算子ということは＋プラス演算子で１＋１というような演算を行っているのと同じです。コードのフローの条件分岐ではなくて、値の場合分けという演算、計算をしているのです。 たとえばtrue ? 999 : 0 と書けば、<条件式>はtrueで真なので、この式の値は999になります。 もちろんfalse ? 999 : 0 ならば、値は０となります。 三項演算子は命令型のif文と比べて可読性が悪いという誤解がありますが、改行すればいいだけで、命令型のif文による条件分岐と関数型の条件演算子の式とを対比すると、 • 命令型　if文

let x; if (true) { x = "true" } else { x = "false" } // x == "true"

• 関数型　条件演算子の式

const x = true ? "true" : "false"; // x == "true"

とかなり条件演算子の式のほうがかなり簡潔に記述できます。 命令型では、まずxという後から中身になにか値を入れる変数をletでとりあえず準備しておいて、if文によってフローを分岐させる、このサンプルコードの場合、かんたんのため条件式がtrueと決め打ちされているので、分岐先の代入命令文により x = "true" と値が代入されています。破壊的代入を行っているわけで、実際このコードでletではなく破壊的代入を明示的に禁止するconstとするとエラーになります。 関数型ではフローをコントロールするのではなく、「値の場合わけ」をします。命令型コードのような x はとりあえず空で、後から命令文によってなにか値が代入される、というフローは存在しません。最初からconstで決め打ちです。決め打ちはしますが、どの値で決め打ちするのかを条件演算子によってその場で場合分けするのです。この場合かんたんのため条件式がtrueと決め打ちされているので、x = "true" と値が決定されます。 偶数と奇数を場合分けするコードは、

const number = 3 const result = (number % 2 === 0) ? "偶数" : "奇数"; console.log(result); //奇数

となり、すべて式の組み立てと宣言で構成されています。 7.4. より洗練され強力なパターンマッチングをつかう if文を条件演算子の式で簡潔に書き直せることは理解できた、では、より複雑な条件を扱うswitch文はどうする？という懸念があることでしょう。これも関数型コードでは当然のように式で構築します。 例えば、switch文を利用して、HTMLのDOMのタグの種類を判別する以下のような命令型のコードがあります。

switch (type) { case 'text': case 'span': case 'p': return 'text'; case 'btn': case 'button': return 'button';}

これは、関数型の式として（オブジェクトメソッドとしての表記ではあるが）書き直せます。

const sanitize = name => match(name) .with('text', 'span', 'p', () => 'text') .with('btn', 'button', () => 'button') .otherwise(() => name);

sanitize('span'); // 'text'sanitize('p'); // 'text'sanitize('button'); // 'button'

こういう形式を、パターンマッチング（Pattern Matching）と呼びます。

いくつかの高水準プログラミング言語には、多分岐の一種で、場合分けと同時に構成要素の取り出しのできる言語機能があり、パターンマッチと呼ばれている。

ts-pattern

Write better and safer conditions. Pattern matching lets you express complex conditions in a single, compact expression. Your code becomes shorter and more readable. What is Pattern Matching?Pattern Matching is a technique coming from functional programming languages to declaratively write conditional code branches based on the structure of a value. This technique has proven itself to be much more powerful and much less verbose than imperative alternatives (if/else/switch statements) especially when branching on complex data structures or on several values. Pattern Matching is implemented in Haskell, Rust, Swift, Elixir and many other languages. There is a tc39 proposal to add Pattern Matching to the EcmaScript specification, but it is still in stage 1 and isn't likely to land before several years (if ever). Luckily, pattern matching can be implemented in userland. ts-pattern Provides a typesafe pattern matching implementation that you can start using today.

より良い、より安全な条件（condition）を書きましょう。パターンマッチングを使えば、複雑な複数の条件を、単一のコンパクトな式（expression）で表現できます。コードが短くなり、読みやすくなります。 パターンマッチングとは何ですか？パターンマッチングとは、関数型プログラミング言語に由来する技術で、値の構造に基づいて条件付きコードの分岐を宣言的に記述するものです。この技術は、特に複雑なデータ構造や複数の値で分岐する場合に、命令型の代替物（if/else/switch文）よりもはるかに強力で、はるかに冗長性が少ないことが証明されています。 パターンマッチングは、Haskell、Rust、Swift、Elixir、その他多くの言語で実装されています。EcmaScript仕様にパターンマッチングを追加するためのtc39プロポーザルがありますが、まだステージ1であり、この先数年は実装されそうにありません（仮に実装されることがあったとしても）。幸運なことに、パターンマッチングはユーザーランドで実装することができます。 ts-patternは、タイプセーフなパターンマッチングの実装を提供しており、今日から使い始めることができます。

素晴らしいですね。 上の関数型コードで大枠のconst sanitize = name =>というのは、ユーザが自由に定義した関数と引数です。 switch/case文に相当する主要なパーツは• match• with• otherwiseの３つです。

match(name) .with('text', 'span', 'p', () => 'text') .with('btn', 'button', () => 'button') .otherwise(() => name);

おそらく多くの読者にとっては初めて見るAPIなので何のことかよくわからないでしょう。 ここで役立つ強力なフレームワークが、二項演算/二項演算子で式を構築するという関数型コードの一貫した理念です。すでに我々が確認したとおり、オブジェクト指向の表記は以下のように二項演算に変換できます。

オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数は、二項演算の右側の被演算子（Operand）になります。

• 'map' は、ArrayとFuncttionからArrayを生み出す二項演算子です。• Array 'map' Function = Array• [1,2,3] ['map'] (f) = [2,3,4]という馴染み深いケースを思い出しましょう。 このAPIは、

Array.of(5) //[5] .map(f) .map(g) .reduce(h);

に非常に近い構造をしています。 オブジェクト指向の言葉で言うと、Array.of() メソッドは、 Arrayインスタンスを生成します。数学の言葉で言うと、Array.of() は単項演算子であり、配列集合を生み出します。5 → [5]そして 'map' は、Arrayである [5] とFuncttionである f からArrayを生み出す二項演算子です。 パターンマッチングの式に当てはめて考えると、

match(name) .with('text', 'span', 'p', () => 'text')

Array.of() が単項演算子であり、配列集合を生み出したのと同様に、match()は単項演算子であり、パターンマッチングの単位となる集合を生み出します。生み出された配列オブジェクトをArray型と表現するならば、パターンマッチングオブジェクトはPatternMatch型と表現しても良いでしょう。 この場合は、String型の引数として渡ってきたnameがPatternMatch型に格上げされた、ということです。これが、二項演算の左側の被演算子（Operand）になります。PatternMatch.with() メソッドあるいは単に 'with' は、二項演算子です。('text', 'span', 'p', () => 'text')が、二項演算の右側の被演算子（Operand）になります。二項演算の生成物は、あたらしいPatternMatch型の値です。 このように、命令型コードでは漫然とswtich/case文として処理していたものが、関数型コードでは二項演算子で式を構築する、というフレームワークに統合されます。 命令型で書いていたswtich/case文のコードは、関数型のコードでは 1 + 2 = 3 1 + 2 + 3 = 6 Array 'map' f = ArrayArray 'map' f 'map' f = ArrayArray 'reduce' f = Object という二項演算の式と同様に PatternMatch 'with' pattern = PatternMatchPatternMatch 'with' pattern 'with' pattern = PatternMatchPatternMatch 'otherwise' pattern = Object という二項演算の式を組み立てる作業となります。 そして、式の組み立ては依存グラフの構成であり、依存グラフ（Dependency graph）を構成する式（関数型コード）を書いてコンピュータに解決してもらうだけなので、その他の余計なことを考慮する必要は原理的にありません。 さて、この素晴らしいパターンマッチングAPIは、前述の通りJavaScript標準では実装されていないのですが、ts-patternというライブラリで提供されています。作者の紹介ブログはBringing Pattern Matching to TypeScript 🎨 Introducing TS-Pattern v3.0です。 https://www.npmjs.com/package/ts-pattern npmでも目下人気急上昇で、JavaScriptにパターンマッチング（Pattern Maching）機能を提供するライブラリとしては品質は傑出しています。 #StateOfJS 2020: What do you feel is currently missing from JavaScript?2020サーベイ:JavaScriptに欠けていると感じるものは？では、

Pattern MachingはTop3となっており、現在のJavaScriptプログラマーにとって特段に需要が高い機能であることが確認できます。 関数型言語としては見做されることはないPythonですら最近では結構強力なパターンマッチングが実装されているようです。Python 3.10の新機能：「構造的パターンマッチ」とは 7.5. 【余談】TC39の没落では、JavaScript言語標準としてパターンマッチング（Pattern Maching）はどうなっているのでしょうか？tc39/proposal-pattern-matching 現在State:1で、多分あと数年はかかるでしょう。というかStage:4まで到達してその後完成するのか？それ以前にTC39プロポーザル版Pattern Matchingは、どのような実装になっているのでしょう？ うーん、なんか文（Statememt）になっていますね・・・元々Pattern Matchingとは関数型プログラミングが発祥であり、式（expression）であるのが普通なのに。ts-patternのコードでは純粋に簡潔に二項演算の式として構築できることとは対照的です。

const sanitize = name => match(name) .with('text', 'span', 'p', () => 'text') .with('btn', 'button', () => 'button') .otherwise(() => name);

これは何を意味するのか？というと、ts-patternライブラリの作者はPattern Matchingがなんたるかという本質とそれによってもたらされる効能、より良い、より安全な条件（condition）を書きましょう。パターンマッチングを使えば、複雑な複数の条件を、単一のコンパクトな式（expression）で表現できます。コードが短くなり、読みやすくなります。パターンマッチングとは、関数型プログラミング言語に由来する技術で、値の構造に基づいて条件付きコードの分岐を宣言的に記述するものです。この技術は、特に複雑なデータ構造や複数の値で分岐する場合に、命令型の代替物（if/else/switch文）よりもはるかに強力で、はるかに冗長性が少ないことが証明されています。を良く理解していてその強い理念と情熱をもって実装しているのに対して、本件のTS39プロポーザルの参加者は、需要がありそうだしやってみよう、標準化されたら自分の功績にもなるし、という功名心（全員がそうではないが筆者が直接やりとりしたこともあるアカウントの参加者（あまりレベルが高いプログラマとは見做せない）を見てたらおそらくそんなところ）で、さらに背景には「JavaScriptはあくまで命令型の文の集まりとして記述されるべきだ」という信念のようなものが共有されており、switch/case文との後方互換性を維持したかったのだろうと想像します。 いずれにせよ将来、仮にパターンマッチング（Pattern Maching）がTC39によって標準化されたとしても、関数型プログラミングを指向するのであれば、ts-patternライブラリを使い続けるべきでしょう。 筆者の体感から言うと、JavaScriptの策定団体であるTC39はもはやまともに機能していません。近頃特に酷くなってきています。私見ですが、プログラミング技術界隈は、設計理念を共有する一握りの極めて強力で機動性の高い小規模の技術者集団によって大きな進歩を成し遂げています。TC39のすべてとはとても言えませんが、多くのプロポーザルでは、まっとうな設計理念を持たず技術水準がけして高いとは見受けられず、名誉欲や承認欲求だけが強いコントロールフリークがあれこれ仕様に口出す行為を大変楽しんでおられて、高い理念と技術力があるライブラリ作者などの主張正論がもはや通らなくなってしまっています。船頭多くして船山に登るの状態です。その結果、当初、高い知見でコミュニティを牽引してきたプログラマが馬鹿らしくなって将来性のあるプロポーザルから離脱してしまっています。それがこのPattern Matchingプロポーザルにもよく反映されています。 #StateOfJS 2020: What do you feel is currently missing from JavaScript?2020サーベイ:JavaScriptに欠けていると感じるものは？の2位は、Standard Libraryですが、これはまさにnodejsとnpmのことですね。全部、外部の誰かが本来JavaScriptに必要な標準機能を提供しているわけです。V8 JavaScriptエンジン上に構築されたランタイム環境としてデファクトスタンダードとなったnodeJS

nodeから利用できるパッケージマネージャとライブラリエコであるnpm

このように外部で実現されたnpmライブラリをWebブラウザで利用するために、最初にBrowserifyが発明され、その後、Webpackなどが登場してきました。この混乱の背景にはブラウザ戦争による標準化の困難さがあったので、TC39の没落というのは公平ではない気がしますし、現在ではES Modules(esm)が登場したので状況は良い方向へ流動的です。もっとも大きな流れはnodeのオリジナルの開発者であるRyan Dahlが、Node.jsに関する10の反省点 - Ryan Dahl - JSConf EUとして、新しいJS/TSランタイムDenoをリリースしました。https://github.com/denoland/denohttps://deno.land/

Denoはnpmから脱却し、標準化されたESModuleを利用しています。もはやWebpack系の回り道は必要ありません。 2020サーベイの1位は、StaticTypingで圧倒的です。これはまさにTypeScriptの登場と人気ぶりに直結しています。JavaScriptに型（Type）をつけて欲しいという要望は昔から強く有りましたが実現することはありませんでした。遅々としたJavaScriptの進歩に業を似やした技術者達は、それぞれ独自のAltJSと呼ばれるJavaScriptの代替となる言語を開発しました。TypeScriptはそのうちMicrosoftのアンダース・ヘルスバーグ (Anders Hejlsberg ）が設計し人気を博し現在主流となったAltJSです。TypeScript/背景

TypeScriptはECMAScript 2015において期待されている機能を先取りするようなものであるともいえる。ECMAScriptの提案にないがTypeScriptに独自に搭載された機能として、静的言語解析を可能にする静的型付け機能(使用するかどうかは選択可能)がある。

#StateOfJS 2020: What do you feel is currently missing from JavaScript?2020サーベイ:JavaScriptに欠けていると感じるものは？第3位のPattern Machingに続く4位はパイプラインオペレータ（Pipeline Operator）です。結構、僅差とは言えて、このあたりが突出しているようです。 パイプラインオペレータ（Pipeline Operator）も例にもれずTC39プロポーザルがあります。tc39/proposal-pipeline-operator現在Stage:2で、最近昇格しましたが、Brief history of the JavaScript pipe operatorJavaScriptパイプオペレータの簡単な歴史でまとめられているように、2015年より、このひとつのオペレータのために議論が紛糾しており現在かなり悪い方向へ迷走中です。パイプラインオペレータ（Pipeline Operator）は、もともと関数型言語であるF#で広く活用されてきた数学的な意味での二項演算子なのですが、非常に愚かなことに、前述の「JavaScriptは命令型の文で書かれなければならない」それが多数派だからという信念の影響で、具体的にはAsync/Await（これ自体が式であるPeomise.then()のSyntaxSugar（糖衣構文）である命令型の文であり、同じ信念のもとに生み出された）との相性が悪い、との理由で長らく提案され続けていたF#Styleは却下され、現在HackStyleなる醜悪なものとなりStage2に進み、コミュニティからの大反発を食らっています。関数型プログラミングコミュニティはHackStyleの偽パイプラインオペレータ（Pipeline Operator）が仮に本当に実装されても受け入れることはないでしょう。これはパターンマッチング（Pattern Maching）とまったく同じ状況と言えなくもないですが、厄介なのは、ユーザーランドレベルのライブラリで上手く提供されて活用できるパターンマッチング（Pattern Maching）とは異なりパイプラインオペレータ（Pipeline Operator）は言語レベルでハードコーディングされた二項演算子なのです。 教訓: もはやTC39はアテにならない。静的型（StaticTyping）、パターンマッチング（Pattern Matching）、パイプラインオペレータ（Pipeline Operator）、それから演算子のオーバーロード（Operator overloading）、演算子のユーザー定義（Custom Operator）など関数型プログラミングを指向する上で本当に欲しい機能がJavaScriptのネイティブ実装として提供される希望はかなり少ないでしょう。しかし、オブジェクト指向への評価の没落と反比例するように関数型プログラミングへの注目度は年々高まり続けている、それはこういうパターンマッチング（Pattern Maching）という関数型由来の技術への需要の高まりという現象を見ても明らかです。 8. 関数型プログラミングで複雑性との闘いに勝利するためのたったひとつの方法8.1. ある式を別の式に交換する

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add)

あるいは

[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]['reduce'](add)

という式を書く このように説明すると、命令型のコードはそんな配列データ[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]ベタ書きなどしていないし、100とか1000とか10万とか大きな数になればどう適応させるつもりなのか？コードの汎用性に欠けるのではないか？という指摘がきっとあることでしょう。 それは実は結構些細なことで、関数型コードはあくまで式なので、その[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]を、具体的な値ではない、より汎用度の高い式に交換してしまえば簡単に解決できる問題です。 目的の配列操作のやり方は複数あるようですが、ES6 - generate an array of numbers任意の数の自然数の配列を得られるnatural関数を用意して

const natural = n => [...Array(n).keys()] .map(a => a + 1);

const add = (a, b) => a + b;const sum = natural(10).reduce(add); console.log(sum); // 55

ベタ書きだった配列の式を natural(10) という別の式へ置き換えれば良いでしょう。 このように関数型プログラミングは、コード全体が式の列挙であり、それぞれの式の一部分も別の式と交換可能です。 同様に、

natural(10)['reduce'](add)

において、reduce は、 • 配列 natural(10) • 関数 add の間の二項演算を司る二項演算子という事実を考えると、左辺オペランドであるnatural(10)を別の値に交換できたのと同様に、右辺オペランドであるaddも別の関数へ交換可能です。 たとえば、加算のかわりに乗算であるmultiplyに交換して、

const multiply = (a, b) => a * b;const product = natural(4).reduce(multiply);// 1 * 2 * 3 * 4console.log(product); // 24

とすることも自由に可能です。コードの堅牢性が担保されたまま、バグの心配をせずに可能です。 8.2. 「等しい（Equality）」という超強力な概念 厳密に正しさが担保されておりバグがないコードを書く超強力な手段として、式の構築にのみ注力する関数型コードを書くことが機能する背景には、式が「交換可能」である、という概念があります。 上の事例では、[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]という具体的な値が、より抽象的で汎用的な構造であった、natural(10)という値に交換できた、さらに、natural(4)という別の値に交換してもコードが壊れないことは事前によくわかっている、addという関数はmultiplyという別の関数に交換してもコードが壊れないことは事前によくわかっている、このあたりの「コードの堅牢性の担保」があるバグのでないコードを書くにあたって大変に強力で重要です。 「交換可能」ということは、数学的にもうちょっと突き詰めて考えてみると、それは「等しい（Eqaulity）」ということです。

In mathematics, equality is a relationship between two quantities or, more generally two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. 数学では、2つの量、より一般的には2つの数学的表現の間の関係で、量が同じ値を持つこと、あるいは表現が同じ数学的対象を表すことを主張することを「等価性」という。

プログラミングでは、[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ＝ natural(10)という値の等価性もあり、もうひとつ、natural(10)という値がnatural(4)あるいは、addという関数はmultiplyという別の関数に交換可能というのは、その型（Type）＝集合が等しい、という原理があります。型（Type）＝集合については、後述しますが、値が等しい、型（Type）が等しい式を構築する、というアプローチは、「コードの堅牢性の担保」があるバグのないコードを書くためのたったひとつの方法と言い切っても過言ではありません。 8.3. ソフトウェア危機に対する工学的アプローチの根本的な問題ソフトウェア危機ということがありました。

ソフトウェア危機（ソフトウェアきき、Software Crisis）とは、高性能化するハードウェアのコストは低下する一方、複雑化するソフトウェア開発のコストは上昇する傾向が続くことにより、将来的にソフトウェアの供給が需要を満たせなくなるという考え方である。この用語は、ソフトウェア工学がまだ十分に確立していなかった頃によく使われた。その根本には、正しく、可読性が高く、検証可能なコンピュータプログラムを書くことが困難であるという事情がある。

ソフトウェア危機の解決手法ソフトウェア危機は（少なくとも一部は）様々な手法や方法論の開発によって解決されてきつつある。 • オブジェクト指向、カプセル化• 構造化プログラミング• ガベージコレクション• アジャイルソフトウェア開発• マルチスレッド・プログラミング• ソフトウェアコンポーネント• ソフトウェアプロトタイピング• デザインパターン• 統合開発環境、RAD• バグ管理システム、バージョン管理システム• 反復型開発• Model View Controllerしかしフレデリック・ブルックスが『銀の弾などない』で記している通り、「本質的な複雑性」に対して生産性を向上させるような技法は存在しないと言われている。

この、フレデリック・ブルックスによる『銀の弾などない』（No Silver Bullet ）というのは、巷でやたらに引用されています。

『銀の弾などない— ソフトウェアエンジニアリングの本質と偶有的事項』（ぎんのたまなどない ソフトウェアエンジニアリングのほんしつとぐうゆうてきじこう、英: No Silver Bullet - essence and accidents of software engineering）とは、フレデリック・ブルックスが1986年に著した、ソフトウェア工学の広く知られた論文である。 原論文は英語である。日本語では『銀の弾丸はない』と、翻訳されることもある。ブルックスは、「銀の弾丸」（Silver Bullet）として、魔法のように、すぐに役に立ちプログラマの生産性を倍増させるような技術や実践 (特効薬) は、今後10年間（論文が著された1986年の時点から10年の間）は現れないだろう、と記載した。 銀の弾とは、銀で作られた弾丸であり、西洋の信仰において狼人間、悪魔を撃退する際に用いるものとされていた。 ブルックスの警句は、非常に多く引用されており、生産性、品質、制御に適用されている。ブルックスは、自身の警句で述べているプログラマの生産性の限界は「本質的な複雑性」（essential complexity）についてのみ当てはまると述べているのであり、「偶有的な複雑性」（accidental complexity）に対する挑戦については支持している。ブルックスは、偶有的な複雑性については著しい改善（おそらく今後10年間で10倍以上）がみられるだろうと述べている。 ブルックスは、この論文で本質的な複雑性に対処するために、次のことを提案している（詳細は#提案を参照） 購入できるものをあえて構築しないようにするために大市場を利用する。ソフトウェア要件の確立に際し、開発循環計画の一部として、迅速なプロトタイピングを使用する。実行と使用とテストが行われるにつれて、より多くの機能をシステムに追加しながら、ソフトウェアを有機的（系統的）に成長させる。若い世代の素晴らしいコンセプトデザイナーを発掘し、育てる。

『銀の弾などない』（No Silver Bullet ）という主張内容については、2021年現在でもソフトウェア業界で広く引用されるわりには、現在の知見で本当にまだ権威として引用できるほどなのか？と考えてみると個人的にはまったく評価していません。 おそらくブルックスの主張はオブジェクト指向全盛にむけた時代においては、たしかにそれは宣伝されるほどには銀の弾丸ではなかった、という意味では正しいです。 オブジェクト指向をはじめとする、数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないという意味では正しい。 • デザインパターン• Model View Controller というのも、まるでソフトウェア開発における冴えた知見の結晶のように持ち上げられることがありますが、これらは数学の範疇外の余剰の工学的発明で、本質的には複雑性を増しているにすぎず、筋の悪い間違った工学的アプローチです。 そして、ブルックスがいう「本質的な複雑性」とは数学のことなど語っているわけではまったくないので、彼の主張は的外れであると言えます。 8.4. 『銀の弾丸』等しくすれば組合せ爆発（Combinatorial explosion）を回避可能『銀の弾などない』（No Silver Bullet ）というのは誤りで、『銀の弾』は実は存在していて、それは「等しい（Equality）」という超強力な概念に他なりません。 ソフトウェア開発、あるいはプログラミングにおける「本質的な複雑性」（essential complexity）とは、ほんとうは数学的な概念で、それは、組合せ爆発（Combinatorial explosion）です。

組合せ爆発（くみあわせばくはつ、英: combinatorial explosion）は、計算機科学、応用数学、情報工学、人工知能などの分野では、解が組合せ（combination）的な条件で定義される離散最適化問題で、問題の大きさn に対して解の数が指数関数や階乗などのオーダーで急激に大きくなってしまうために、有限時間で解あるいは最適解を発見することが困難になることをいう。

念の為ですが、解決したい課題の対象が本質的に原理的に内在している組み合わせ爆発のことではなく、プログラマが書いてしまいがちで、不注意な、あるいは、不適切な工学的アプローチによるコード自体が本質的には回避可能であるのにもかかわらず、非合理的に、無用に、組みわせ爆発を起こしている、ということです。 無用な組合せ爆発を回避するためには、可能な限り要素を減らすこと、そして何より肝要なことは、本質的に等しいものは、等しいものとして徹底的に扱うこと、さらに必ずしも等しくなければならない要請はなくても、等しいものとして扱うことができるならば等しくする、ということです。 要素が1つしかなければ、組み合わせというのが原理的に存在しないので、組合せ爆発による問題など起こりようがありません。しかし、それぞれの要素に区別があるときは、指数関数的に組み合わせ爆発が起こり収集はつかなくなります。 数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないのですが、裏を返すと「唯一正しい工学的アプローチ」『銀の弾丸』とは、組合せ爆発を回避する「等しくする」という数学的アプローチです。実際これはソフトウェア開発に限らない一般的な工学的な問題として死活問題なので、工業規格という人類の経験則による知見が存在しています。ISO規格（国際標準化機構）があり、JIS（日本）など各国に規格が決定されています。 身近なところでは、電気のコンセントプラグがあり、特にプログラマにとっては、USB規格があります。

ユニバーサル・シリアル・バス（英: Universal Serial Bus、略称：USB、ユーエスビー）は、コンピュータ等の情報機器に周辺機器を接続するためのシリアルバス規格の1つ。ユニバーサル（汎用）の名の示す通り、ホスト機器にさまざまな周辺機器を接続するためのペリフェラルバス規格であり、最初の規格となるUSB 1.0は1996年に登場した。現在のパーソナルコンピュータ周辺機器において、最も普及した汎用インターフェース規格である。

もちろん、Appleのように独自の規格、つまり自前機器のエコだけで完結すれば良いだろう、というのもひとつの主張ではありますが、最近排除されて消費者に歓迎された事案は記憶に新しいところです。EU スマートフォンの充電器をUSB Type-Cへ統一へ（iPhoneのLightningケーブル排除へ） USBなどを使っているとわかりますが、こういう「等しさ」が担保されている概念はBuilding blockになります。その定められた規格内に収まってさえおれば、それらは「等しい」と見做され、自由自在に組み合わせても壊れる心配がありません。LEGOもそれ自体がBuilding blockであり単一の接続規格で、自由自在に構築可能です。

そして、関数型コードの式においては、実際に、

const multiply = (a, b) => a * b;const product = natural(4).reduce(multiply);// 1 * 2 * 3 * 4console.log(product); // 24

reduceという二項演算子の左右オペランドはあらかじめ型（Type）が規定（規格化）されているので、規格に合致してさえおれば、別の値、式に置き換えても全く問題がないことは予め保証されています。逆に、TypeScriptで、タイプエラーが出るということは、間違った型、間違った規格の組み合わせを行ったということになります。 そして、繰り返しとなりますが、二項演算子というのは、関数のことなので、根源的には関数には厳密な型がある、ということにほかなりません。この事実については、後述する関数それ自体の解説の章で詳説します。 根源的には、コードの要素を等しく保つというアプローチで、コードをUSBデバイスやLEGOブロックのように自由自在に組み合わせてもコードは壊れないと担保される、バグのでないメンテナンス性の高いコードをプログラミング可能となります。 実際にこれだけJavaScriptに型付けするTypeScriptが絶大な支持を得ており、Rustなどモダンな言語でも型があたりまえな現状において、型（Type）の等しさを担保することは、銀の弾丸（SilverBullet）だ、と主張されることは滅多にありません。おそらく、ただ『銀の弾などない』（No Silver Bullet ）とさえ発言しておけば、有る一定の論争がある場所で曖昧な玉虫色の決着をつけることに有用な方便としてだけ乱用されており、そこそこ達観した知見のあるポーズを取ることができるからだろうと想像するしかありませんが、現代においては、あまり意味のない言及です。 型（Type）とは、等しくする効用の対象として顕著な事例ですが、「等しい（Equality）」という概念の超強力さはもっと一般的なもので他にも色々あるのでそれについては別に後述します。とりあえず当面は型のことを説明していきましょう。 9. 型（Type）は何故そんなに役に立つのか？そもそも型（Type）とは何か？9.1. JavaScriptコミュニティでは型（Type）が圧倒的に重要視されている #StateOfJS 2020: What do you feel is currently missing from JavaScript?2020サーベイ:JavaScriptに欠けていると感じるものは？では、

Static Typing（静的型付け）が圧倒的な需要があります。 その根本的な理由は、

プログラミングでは、[1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ＝ natural(10)という値の等価性もあり、もうひとつ、natural(10)という値がnatural(4)あるいは、addという関数はmultiplyという別の関数に交換可能というのは、その型（Type）＝集合が等しい、という原理があります。型（Type）＝集合については、後述しますが、値が等しい、型（Type）が等しい式を構築する、というアプローチは、「コードの堅牢性の担保」があるバグのないコードを書くためのたったひとつの方法と言い切っても過言ではありません。

関数型コードの式においては、実際に、 const multiply = (a, b) => a * b;const product = natural(4).reduce(multiply);// 1 * 2 * 3 * 4console.log(product); // 24 reduceという二項演算子の左右オペランドはあらかじめ型（Type）が規定（規格化）されているので、規格に合致してさえおれば、別の値、式に置き換えても全く問題がないことは予め担保されています。逆に、TypeScriptで、タイプエラーが出るということは、間違った型、間違った規格の組み合わせを行ったということになります。

根源的には、コードの要素を等しく保つというアプローチで、コードをUSBデバイスやLEGOブロックのように自由自在に組み合わせてもコードは壊れないと担保される、バグのでないメンテナンス性の高いコードをプログラミング可能となります。

ということです。9.2. 巷によくある、よくわからない、型（Type）の説明 多くのプログラマーは多かれ少なかれ「どうやらプログラミングの世界には型（Type）があって、それをコードの中で明示的に宣言するかしないかが、ときどき大きな議論になっているようだ」というところから型（Type）の概念に遭遇することでしょう。

JavaScriptは動的型付け言語（dynamically typed language）です。

動的型付け（どうてきかたづけ、英: dynamic typing）とは、プログラミング言語で書かれたプログラムにおいて、変数や、サブルーチンの引数や返り値などの値について、その型を、コンパイル時などそのプログラムの実行よりも前にあらかじめ決めるということをせず、実行時の実際の値による、という型システムの性質のことである。 また、そのような性質の言語を、動的型付き言語（どうてきかたつきげんご、英: dynamically typed language）という。これに対し、型は実行前に決まる、というのが静的型付けである。型推論を利用していて、構文上は型の記述が省略可能な言語もあるが、そういった言語も静的型付けである（MLなど）。

TypeScriptは静的型付け言語（statically typed language）です。

静的型付け（せいてきかたづけ、英: static typing）は、プログラミング言語で書かれたプログラムにおいて、変数や、サブルーチンの引数や返り値などの値について、その型が、コンパイル時など、そのプログラムの実行よりも前にあらかじめ決められている、という型システムの性質のことである。 また、そのような性質の言語を、静的型付き言語（せいてきかたつきげんご、英: statically typed language）という。これに対し、型は実行時の実際の値による、というのが動的型付けである。型推論を利用していて、構文上は型の記述が省略可能な言語もあるが、そういった言語も静的型付けである（MLなど）

では、その型（Type）というものは何なのか？Wikipediaなどで調べてみると、 データ型

データ型（データがた、data type）とはコンピュータプログラミングや計算機科学において、データ値の性質を定義するための表現であり、コンパイラやインタプリタにそのデータ値の用法を宣言するための機能である。単に型（かた、type）とも呼ばれる。データ型は、関数や演算子に対するデータ値の適用の可否や、変数に対するデータ値の代入や束縛の可否を判定して、式やステートメントによる計算実行を制限する。データ型を基準にした計算可能性を規則化する形式手法は、型システムと呼ばれている。データ型は型理論視点の値の集合と同義になり、式・関数・変数の評価後の代数としても用いられる。ほとんどのプログラミング言語は、整数型・浮動小数点型・論理型・文字型といった基本データ型を備えており、また一定のデータ構造に付与される複合データ型を備えている。言語によってはポインタ・シンボル・式・関数にもデータ型は付与される。

型システム

型システム（英: type system）は、計算機科学およびコンピュータプログラミング分野において、主にデータを扱うための数々の規則の集合から成立した形式体系であり、プログラム内の様々な要素に型（type）と呼ばれる特性を付与する仕組みである。型を付与される対象としては基本的なデータ値のほか、変数、式、関数、オブジェクト、モジュールなどが挙げられる。型の付与は、データの分類を成立させてデータ型を表現するほか、それらデータ型の規則的な集合を表わしたデータ構造の形式的分類も成立させる。型システムの意義は、プログラム要素を分類し、各分類の識別法則の一貫性および分類間関係の整合性を保証して、フォールトアヴォイダンスの視点からプログラムエラーの発生を抑止することにある。型システムは数学基礎論または数理論理学で扱われる型理論に基づいて構築されたコンピュータプログラミング用の形式手法である[1]。型とは「データ型」も参照プログラミング言語はさまざまな値を扱う。代表的かつ最も原始的なものは数値や文字列だが、一般的に有限の資源制約があるコンピュータにとって都合のよい内部表現が使われ、例えば数値には32ビットや64ビットといった固定サイズの整数型や浮動小数点数型が、文字列には特定の文字コード集合によって符号化された整数値の羅列（文字配列）が使われることが多い。文字列の表現には最後の文字（番兵）に0を使用するゼロ終端文字列（ヌル終端文字列）が使われることもあれば、長さ情報を別途整数値で保持する複合データ構造が使われることもある。三角関数は浮動小数点数を引数にとり浮動小数点数を返す。先頭の文字を大文字にする関数は文字列を引数にとり文字列を返す。ユーザーからの入力を数値として扱うためには、文字列を解釈して数値を返す関数が必要である。ここで、3.14 や "hoge" といった値について「浮動小数点数」や「文字列」といった種類に分類して扱っているが、同じ種類の値であれば同じ操作（演算）が可能である。この「値の種類」が型（データ型）である。

初学者というか多くの、ほとんどのプログラマーが型（Type）とは何か？と概念を習得したいときに、この説明でわかるとは到底思えません。もしかしたら説明している当事者が事象の表面をなぞって見せているだけで本当のことは何もわかっていない危険性が大きいです。 9.3. わかりやすい、型（Type）の説明 型（Type）とは集合（Set）のことです。

数学における集合 (しゅうごう、英: set, 仏: ensemble, 独: Menge) とは、大雑把に言えばいくつかの「もの」からなる「集まり」である。集合を構成する個々の「もの」のことを元 (げん、英: element; 要素) という。 数学において、集合とは要素の集まりである。集合を構成する要素は、数、記号、空間上の点、直線、その他の幾何学的形状、変数、さらには他の集合など、あらゆる種類の数学的対象となりうる。集合は有限個の要素を持つこともあれば、無限個の要素を持つこともある。2つの集合が等しいのは、正確に同じ要素を持つ場合に限られる。

ブリタニカ百科事典

集合とは、数学や論理学において、対象物（要素）の集まりのことで、数学的なもの（例えば、数や関数）である場合もあれば、そうでない場合もある。集合の直感的なアイデアは、おそらく数のそれよりも古いものである。例えば、動物の群れのメンバーは、袋の中の石と一致させることができるが、どちらの集合のメンバーも実際には数えられない。この概念は無限にまで広がる。例えば、1から100までの整数の集合は有限であるが、すべての整数の集合は無限である。

Type theory versus set theory型理論 vs 集合論

Alternately, we could change our terminology so that what we have been calling “types” are instead called “sets”.あるいは、これまで「型」と呼んでいたものを「集合」と呼ぶように用語を変更することもできます。 Thus, words like “type” and “set” and “class” are really quite fungible. This sort of level-switch is especially important when we want to study the mathematics of type theory,このように、「型」や「集合」や「クラス」などの言葉は、実はかなり代替可能です。このようなレベルの切り替えは、型理論の数学、つまり型理論の数学を研究するときには特に重要です。

以上は、nLab記事からの引用文です。

nLab は、数学・物理学・哲学の研究レベルの内容について扱ったウィキである。nLabはMathOverflowにおいて、質問前にチェックするべき標準的なオンラインの数学文献の1つとしてリストされている。多くの質問と解答が、nLabを背景資料として用いている。また、nLabはバイエズがアメリカ数学会（American Mathematical Society）に投稿した数学ブログのレビュー記事の中で言及されている2つのウィキのうちの1つである。

Types as Sets集合としての型

One of the most important techniques in Elm programming is to make the possible values in code exactly match the valid values in real life. This leaves no room for invalid data, and this is why I always encourage folks to focus on custom types and data structures.In pursuit of this goal, I have found it helpful to understand the relationship between types and sets. It sounds like a stretch, but it really helps develop your mindset! Elmプログラミングで最も重要なテクニックの一つは、コード内の値を実際に有効な値と正確に一致させることです。これでは無効なデータを残す余地がないので、私は常にカスタム型やデータ構造に注目することを推奨しています。この目的を追求するにあたって、型（types）と集合（sets）の関係を理解しておくことが役立つことを私は発見しました。余計なことのように聞こえますが、それは貴方のマインドセットの形成に本当に役立つのです！

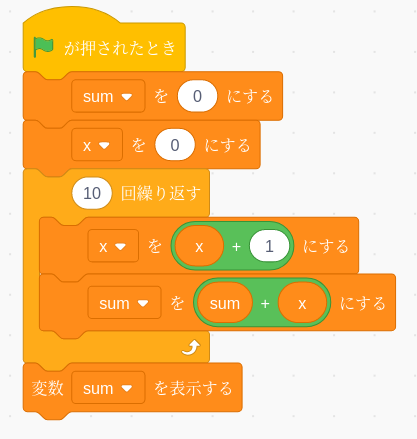
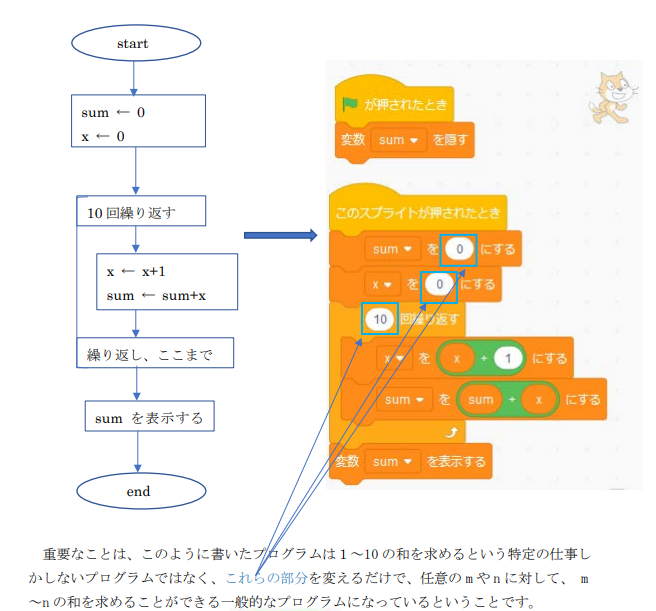
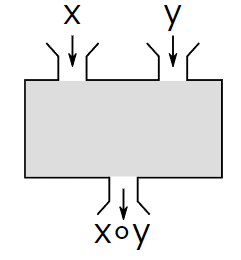
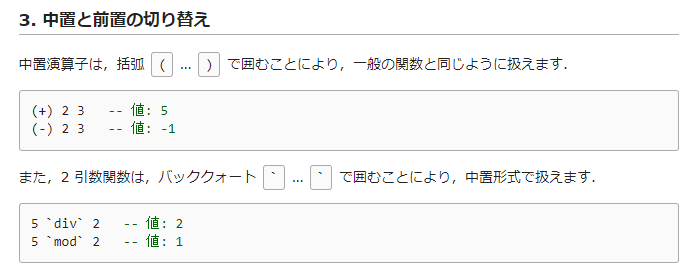
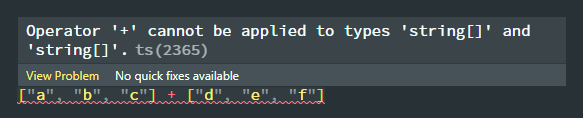
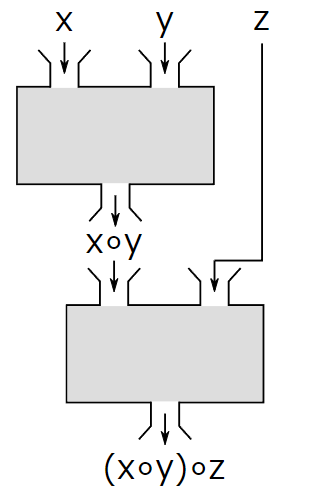
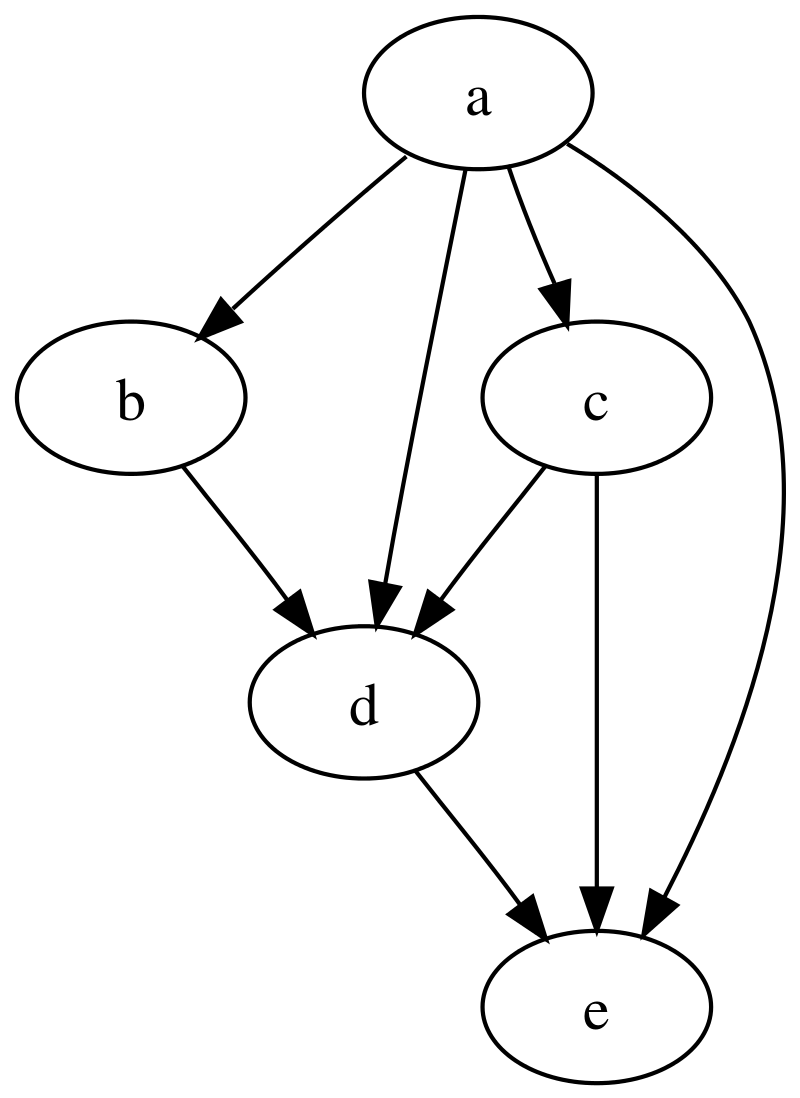
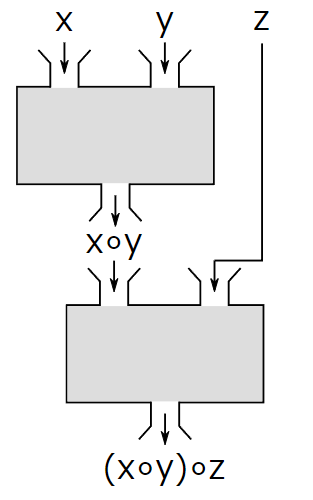
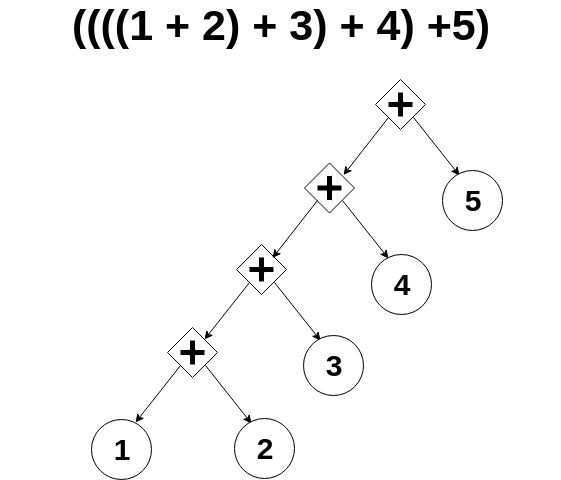
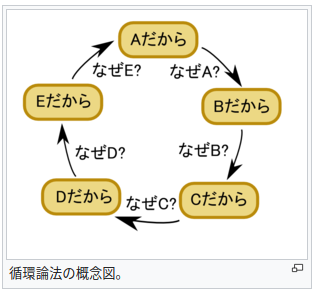
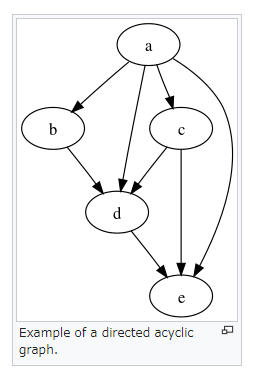
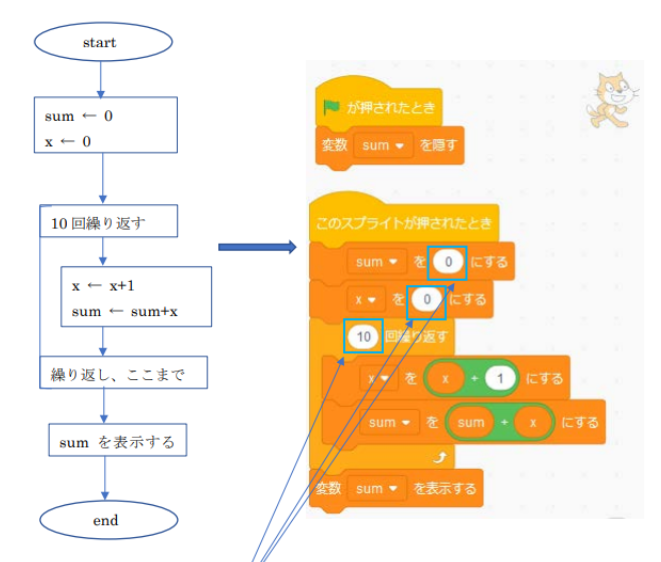
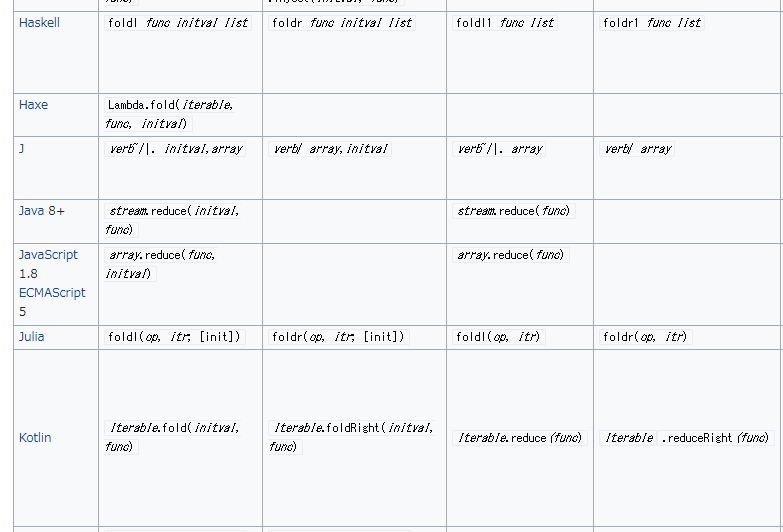
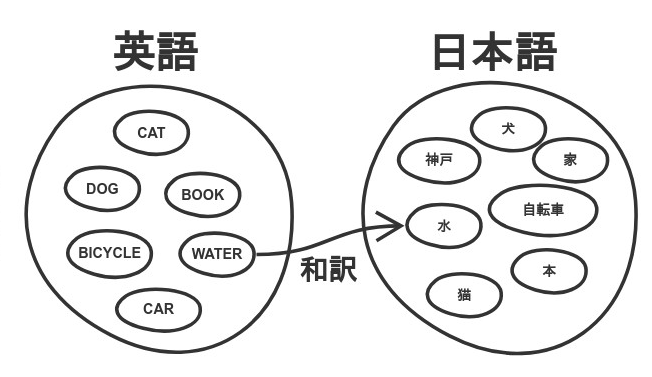
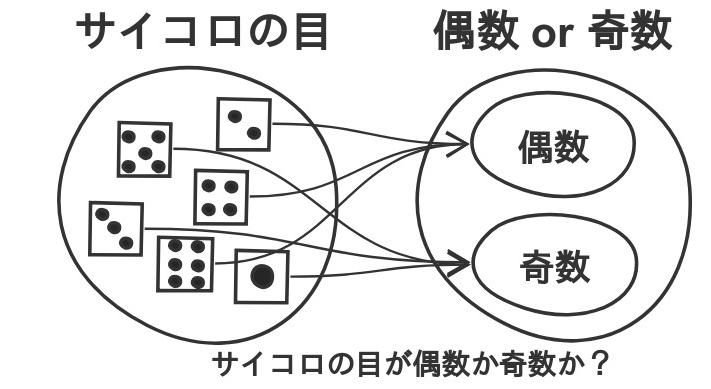
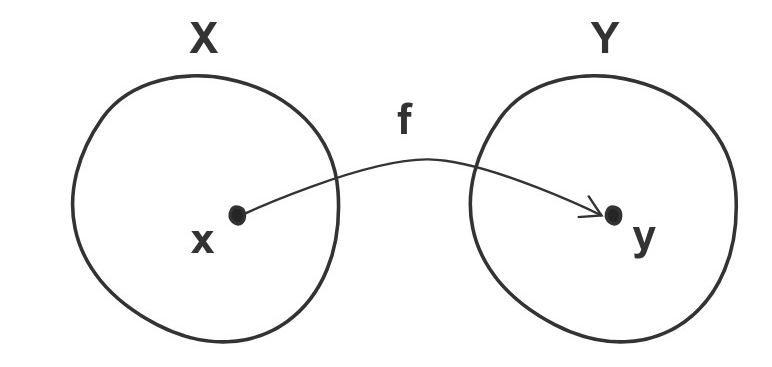
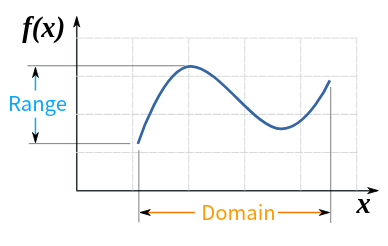
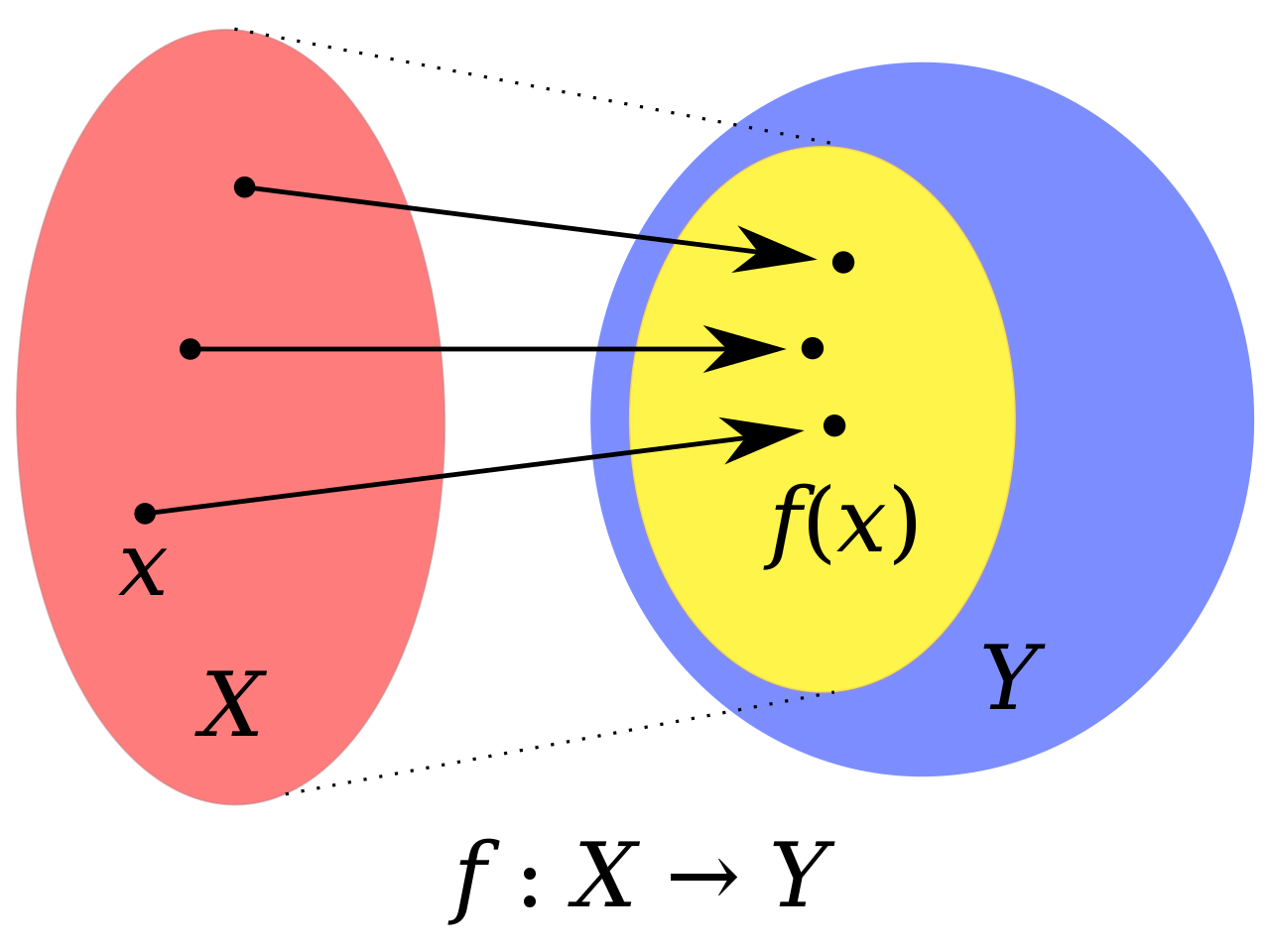
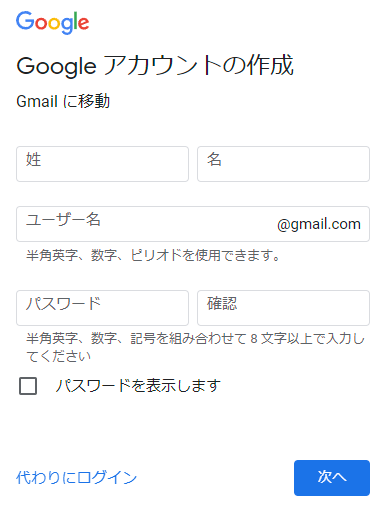
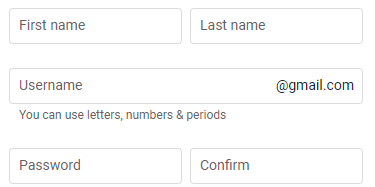
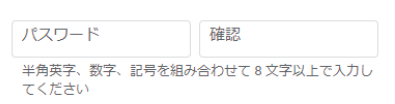
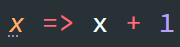
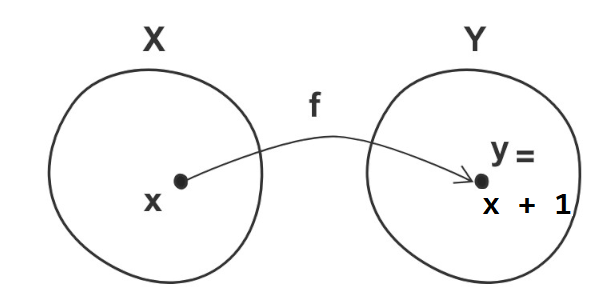
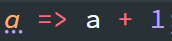
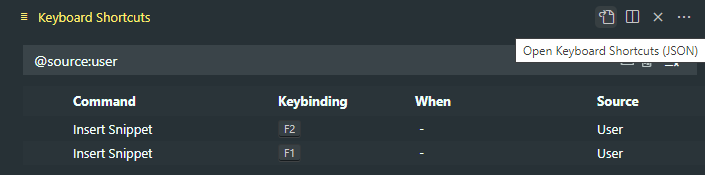
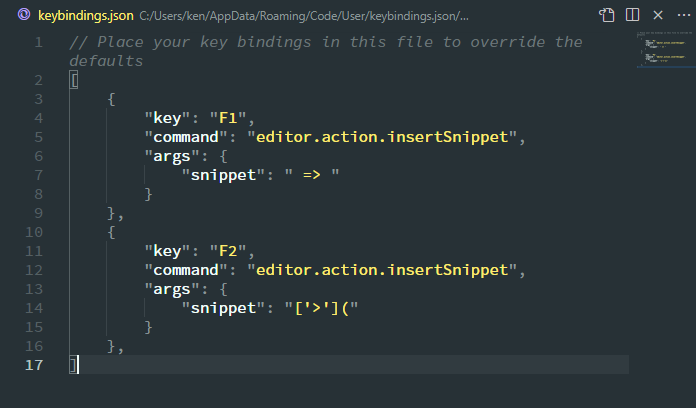
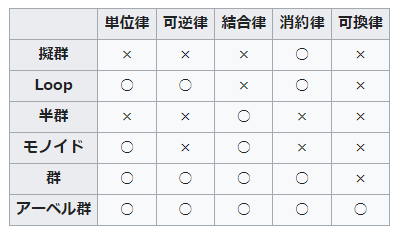
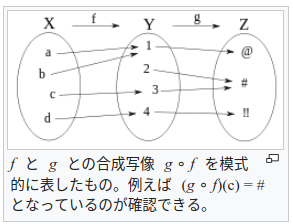
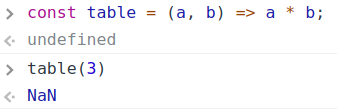
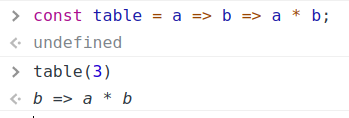
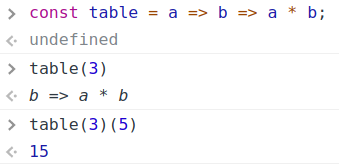
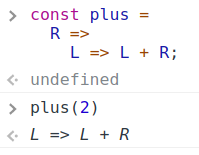
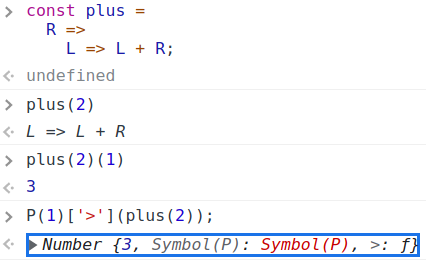
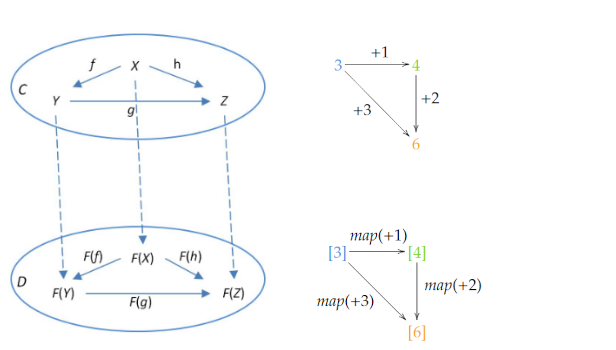
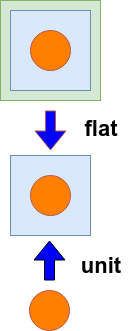
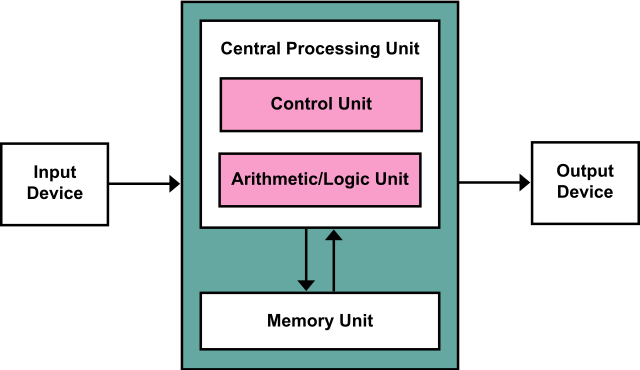
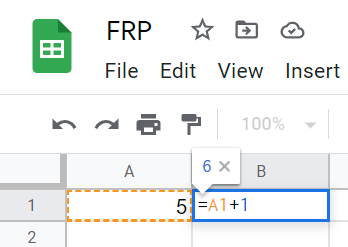
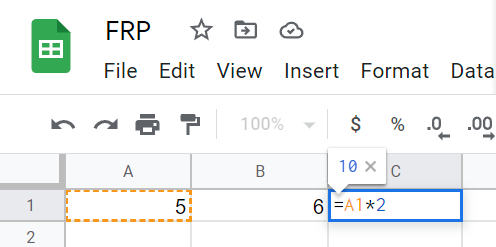
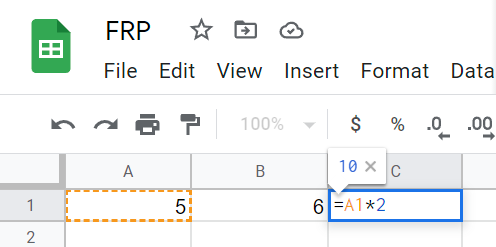
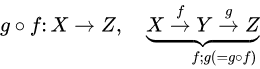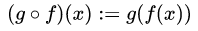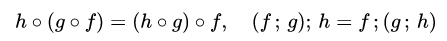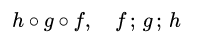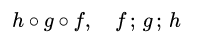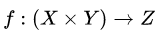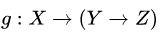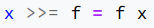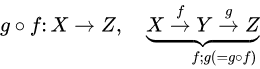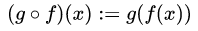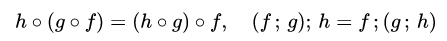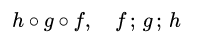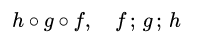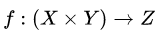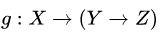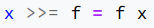集合（Sets）型（Type）は値の集合（Set）と捉えることができる • Bool は集合 { True, False }• Color は集合 { Red, Yellow, Green }• Int は集合 { ... -2, -1, 0, 1, 2 ... }• Floatは集合 { ... 0.9, 0.99, 0.999 ... 1.0 ... }• String は集合 { "", "a", "aa", "aaa" ... "hello" ... } つまり、型（Type）の文脈で x : Bool というとき、それは、x は集合 { True, False } の要素というのと同じです。

型（Type）をこのような集合（Set）として考えることは、ある言語が人によって「簡単」「制限がある」「間違いやすい」と感じる理由を説明するのにも役立ちます。例えば Java - BoolやStringといったプリミティブな値があります。そこから、異なる型のフィールドを固定的に持つクラスを作ることができます。これはElmのレコードによく似ていて、カーディナルを掛け合わせることができます。しかし、足し算をするのはなかなか難しい。サブタイピングを使えばできますが、かなり手の込んだ作業になります。つまり、Elmでは簡単なResult Bool Colorも、Javaではかなり大変なのです。5のカーディナリティを持つ型を設計するのは非常に難しく、しばしばトラブルの価値がないように思われるため、Javaを「制限的」と感じる人もいると思います。 JavaScript - ここでも、BoolやStringといったプリミティブな値があります。ここから、動的なフィールドセットを持つオブジェクトを作成することができ、カーディナリティを増やすことができます。これはクラスを作るよりもはるかに軽量です。しかし、Javaのように、加算を行うことは特に簡単ではありません。例えば、Maybe Intをシミュレートするには、{ tag: "just", value: 42 } や { tag: "nothing" }のようなオブジェクトでMaybe Intをシミュレートすることができますが、これは実際にはカーディナリティの掛け算です。これでは、実際に有効な値のセットと正確に一致させるのはかなり困難です。このように、カーディナリティが(∞×∞×∞)の型を設計するのは非常に簡単で何でもカバーできるので、JavaScriptを「簡単」と感じる人がいる一方で、カーディナリティが5の型を設計するのは実際には不可能で、無効なデータのためのスペースがたくさんあるので、JavaScriptを「エラーが多い」と感じる人もいるのではないでしょうか。 面白いことに、いくつかの命令型言語にはカスタム型があります。Rustがその良い例です。Rustでは、CやJavaから得られる直感に基づいて、これらをenumと呼んでいます。そのため、RustではElmと同じように簡単にカーディナリティを追加することができ、同じような利点があります。 ここで言いたいのは、型の「追加」は一般的に非常に過小評価されているということです。「集合としての型」として考えることで、ある言語設計がなぜある種のフラストレーションを生むのかを明確にすることができます。

これは、TypeScriptではなく、Elm言語作者によるドキュメントなのですが、型（Type）の知見を深めたいとき、示唆に富んでいる内容なので、Google翻訳なりを活用しながらでも全文を読むことをお勧めします。 9.4. スーパーイディオム分野にまたがって、基本、同じ概念を違う用語で表現しています。

型理論（Type theory）	型（type）	関数（function）/ 写像（map）
集合論（Set theory）	集合（set）始集合（domain）と終集合（codomain）	写像（map）
解析学（Analysis）	定義域（domain）と値域（range）と終域（codomain）	関数（function）
代数学（Algebra）	集合（set）/ 被演算子（operand）	演算子（operator）
オブジェクト指向（Object-oriented programming）	オブジェクト（object）	メソッド（method）
圏論（Category theory）	対象（object）/ 圏（category）	射（morphism）

情報処理・プログラミング

データ（data）

処理（operation）

このなかで、最も根底となる、すべての概念の包括的な枠組みが圏論（Category theory）で、これまで永らく数学の基礎であった集合論でさえも圏論の言葉で再定義されます（集合の圏（category of sets）における射（morphism）は関数（function）になる）。 型（Type）とは集合（Set）のこと。関数（Function）と演算子（Operator）は本当は同じもの。オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数は、二項演算の右側の被演算子（Operand）になります。 と既に明確にしたとおり、本稿の方針は、二項演算子(Binary operatior)を最大限に活用することなので、このなかでどの分野の言葉をもってコードを書いていくのか？となると、当然、代数学（Algebra）になります。 しかし同時に明確にしたとおり、その二項演算子は、関数（Function）と同じものであり、さらに集合論の写像（map）と同じものであるので、なにはともあれ、そこの基礎を固める必要があります。 10. 関数（Function）10.1. 関数の具体例 関数（Function）は、２つの型（Type）＝集合（Set）の間の一方向の関係として定義されています。矢印があるのは一方向の関係である、ということを如実に示しています。

国都市首都関数 ここでは、国と都市（首都）という２つの集合の間の一方的な関係を定義しています。 「別に何も一方向じゃなくても良いんじゃない？双方向の矢印でも・・・」という自由な発想はもちろんアリですが、そうなると、二項関係（Binary relation）という、もっと一般的な（ゆるい）数学的概念になります。 二項関係にはいろんな種類があるのですが、そのうち、あくまでこういう一方向で答えがバシッと出てくる保証がある関係を関数関係あるいは単に関数（Function）と呼ぶわけです。逆方向については何の保証もありません。逆方向にについて何か保証がある関係の二項関係というのはもちろん存在しています。 例えば、色がついている自由な図形という集合があります。色関数で、色の集合の要素には、必ずひとつに対応しますが、逆方向に対応することは保証されていない、そういう一方通行の関係が関数です。

こういうのは、しばしばブラックボックスのように抽象化されて、 単項関数（Unary function）なら、

一項演算子は１引数の関数(Unary function)と対応するのがわかります。

!(true) // falsef(true) // false

単項演算（Unary operation）とおなじものであり、 二項関数（Binary function）なら、

これは、二項演算（Binary operation）となります。 つまり、関数は一方通行で、必ずなんらかの答えが出てくる、というのは、二項演算 1 + 2 = 3 と必ず答えが出てくる、という事実と直結しています。 こういう二項演算というものは算数の計算なのだから答えが出てくるのが当たり前、という日常生活の刷り込みがありますが、そもそも演算の対象となっている集合（被演算子）というのは、わかりやすい、型（Type）の説明で示したとおり、別に日常生活でいうところの数字である必要もなく、このように国でも都市でも色なんでも良いのですから、いかなる概念であっても、関数で一方向へ演算している、ということになります。 首都関数を使う

イギリスイギリスの首都は？ロンドン日本日本の首都は？東京首都関数首都関数イギリス 国をインプットしたらその通貨をアウトプットする 通貨関数

国通貨関数通貨 通貨関数を使う

イギリスイギリスの通貨は？ ポンド日本日本の通貨は？ 円通貨関数通貨関数 英単語をインプットしたら対応する日本語の単語をアウトプットする 英和関数

英単語英和関数日本語の単語英和辞書＝和訳する関数 英和関数を使う

BOOKBOOKの和訳は？本WATERWATERの和訳は？水英和関数英和関数 英和辞書もそうですが、データベースは関数として使えます。 Googleの検索エンジンは巨大なデータベースで、膨大なWeb記事がランキングされてストックされています。Google検索も、検索ワードがインプット、検索結果がアウトプットの関数です。 検索ワードをインプットしたら検索結果をアウトプットする Google関数

検索ワード検索結果Google関数=検索エンジン Google関数を使う

緑茶Google関数=検索エンジン日経平均株価Google関数=検索エンジン 手書き画像をインプットしたら数字をアウトプットする AI関数

手書き画像AI関数手書き画像から数字を判別する機械学習モデル数字 AI関数を使う

AI関数手書き画像から数字を判別する機械学習モデル３AI関数9事前に数万以上の手書き画像のデータを使って、アウトプット精度の高い関数を学習させておく（機械学習）

10.2. かんたんにテーブルで表される関数 簡単な構造の関数は単純なテーブル（表）で表現できます。 首都関数

インプット	アウトプット
イギリス	ロンドン
日本	東京
フランス	パリ
アメリカ	ワシントンD.C.
・・・	・・・

通貨関数

インプット	アウトプット
イギリス	UKポンド
日本	円
フランス	ユーロ
アメリカ	USドル
・・・	・・・

英和関数

インプット	アウトプット
CAT	猫
DOG	犬
WATER	水
BYCYCLE	自転車
・・・	・・・

他方でGoogle検索やAI(機械学習)のコンピュータビジョンの関数は単純なテーブルで表現するのは極めて困難でしょう。 10.3. テーブルからかんたんにグラフにできる関数 「気温　東京　年間」でGoogle検索すると、「過去の平均気温」という「データベース系の関数のテーブル」が出てきます。 気温関数

よく見ると、グラフというタブも用意されています。 気温関数(グラフ)

このように、• インプットが数値• アウトプットが数値の場合、• インプットをX軸• アウトプットをY軸とした２次元平面上にプロットし、関数をグラフとして視覚化すれば便利なケースがあります。 念の為に繰り返しますが今まで見てきたように、関数はインプットとアウトプットがシンプルなテーブル(表)で表現できて、なおかつXY平面上にプロットが可能な数値であるとは限定されているわけではないので、あくまで特別なケースでしかありません。 10.4. 数学法則を使う関数 Google検索、それから手書き文字などを識別するコンピュータビジョンのAIも含め、過去に蓄積されたデータベースを利用する関数がある一方で、そのようなデータベースを利用しない、必要としない関数もあります。数学法則を使う関数です。数学法則というのは、なぜか最初から存在しているので、人為的に蓄積しておくべきデータは必要ありません。 絶対値を求める関数を使うa|-5| = 5|8| = 8

-5 | |58 | |8 ここで絶対値を求める関数というのは単項演算子ですね。 ２倍する関数を使うa1 × 2 = 22 × 2 = 4

1 224×2 ×2 ２倍する関数(テーブル表現)

インプット	アウトプット
1	2
2	4
3	6
4	8
・・・	・・・

これは、気温のテーブルを二次元平面にプロットしてグラフにしたら役立ったのとまったく同じ原理で、XY軸のグラフにプロットできます。 ２倍する関数(XY軸のグラフ)

どうせ、X軸とY軸の二次元平面にプロットすることも見越して、一石二鳥を狙うような感じで、数学世界の慣習で、 • インプット側の数値の変数はXとする• アウトプット側の数値の変数はYとする• ことに暗黙の了解としてなっており、変数XとYのテーブルで関数表現がされることも多いです。 ２倍する関数(XY変数のテーブル)

X	Y
1	2
2	4
3	6
4	8
・・・	・・・

義務教育では、y=2x という方程式が２倍する関数になる、とヤブから棒に教えられることが多く、世の中高生が混乱しているようです。 10.5. 数式だけが関数なのではない 「数学法則を使う関数」と例のひとつであげたということは、数式だけが関数ではないことを意味します。 関数 (数学)には、

かつては、ある変数に依存して決まる値あるいはその対応を表す式の事であった。この言葉はライプニッツによって導入された。その後定義が一般化されて行き、現代的には数の集合に値をとる写像の一種であると理解される。 この f(x) という表記法は18世紀の数学者オイラーによるものである。オイラー自身は、変数や定数を組み合わせてできた数式の事を関数と定義していたが、コーシーは上に述べたように、y という変数を関数と定義した。 現代的解釈ディリクレは、x と f(x) の対応関係に対して一定の法則性を持たせる必要は無いとした。つまり、個々の独立変数と従属変数の対応そのものが関数であり、その対応は数式などで表す必要はないという、オイラーとは異なる立場をとっている。 集合論的立場に立つ現代数学では、ディリクレのように関数を対応規則 f のことであると解釈する。それは二項関係の特別の場合として関数を定義するということであり、その意味で関数は写像の同義語である[注釈 2]。より細かく、「数」の集合への写像に限る場合もある[注釈 3]。

だいたい筆者が義務教育から高校にかけて数学の授業で「関数」を教わった記憶で言うと、おおよそ「関数」とは、オイラーが主張していたような数式として導入されたように思います。ところが実際には現代的な解釈では、そうではない、本稿であげたようなテーブルのようなものでも関数で、概念的には集合論の写像のイメージが正しいのです。 次の章では、写像（Map）について調べましょう。 11. 写像（Map）11.1. 写像（Map）という概念の定義https://en.wikipedia.org/wiki/Map_(mathematics)

In mathematics, a map is often used as a synonym for a function, but may also refer to some generalizations. 数学では、写像(map)は関数(function)の同義語として使われることが多いですが、いくつかの一般化を指すこともあります。

https://ja.wikipedia.org/wiki/写像

写像（しゃぞう、英: mapping, map、 仏: application）とは、二つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことである。関数、変換、作用素、射などが写像の同義語として用いられることもある。 ブルバキに見られるように、写像は集合とともに現代数学の基礎となる道具の一つである。現代的な立場では、「写像」と（一価の）「関数」は論理的におなじ概念を表すものと理解されている(略)

ざっくり、写像とは関数を別の観点から描き直したものです。

イギリスの首都は？ロンドン首都関数イギリス国都市首都関数 首都関数

イギリスイタリアアメリカフランス　日本　パリワシントンDCニューヨーク　東京ロンドン　大阪　ローマワシントンDC国都市首都 関数 = 写像( function = map )集合(set)集合(set)こう描き直してみると、当初の関数の図解は直感的で、とっつきやすいものの、集合（型）と要素である値がごっちゃになっていて、どこからどこまでが関数なのかも適当に議論していたことが明確になります。 英和関数（英和写像）の場合はもちろん、こうなります。

「サイコロの目が偶数か奇数か？」と振り分ける事も関数（写像）です。

一般化して、

集合 X の各要素 x に集合 Y の1つの要素 y を対応させる規則をXからYへの写像=関数と呼びます。11.2. 写像（Map）と集合（Set）と型（Type）もちろん集合（Set）とは、型（Type）のことなので、TypeScriptの型定義は、 型（type）X から型（type）Y への写像のとき

type FunctionType = (x: X) => Y;

型 Country から型 City への写像のとき

type FunctionType = (x: Country) => City;

型 English から型 Japanese への写像のとき

type FunctionType = (x: English) => Japanese;

型 number から型 number への写像のとき

type FunctionType = (x: number) => number;

より具体的なコードとしては

type Plus = (x: number) => number;const f: Plus = x => x + 1;

サイコロ関数では型 Dice から型 Even | Odd への写像のとき

type DiceFunction = (x: Dice) => Even | Odd;

サイコロ関数のフルコード

const even = "even";const odd = "odd"; type Even = typeof even;type Odd = typeof odd; type Dice = 1 | 2 | 3 | 4 | 5 | 6; type DiceFunction = (x: Dice) => Even | Odd; const evenOdd: DiceFunction = x => x % 2 === 0 ? even : odd; log(evenOdd(5)); // "odd"

11.3. 型（type）集合（set）写像（map）関数（function）定義域（domain）値域（range）終域（codomain） 型とは集合のことであり、二つの集合が与えられたときに、一方の集合の各元に対し、他方の集合のただひとつの元を指定して結びつける対応のことを写像と呼び、写像が関数と同じ概念である、とわかりました。 では、関数では、集合という用語を使っているのか？と言うと、中学の数学の授業を思い出してもらえればわかりますが、使われていないことが多いです。 複数の分野にまたがって、基本、同じ概念を違う用語で表現しています。

型理論（Type theory）	型（type）	関数（function）/ 写像（map）
集合論（Set theory）	集合（set）始集合（domain）と終集合（codomain）	写像（map）
解析学（Analysis）	定義域（domain）と値域（range）と終域（codomain）	関数（function）
代数学（Algebra）	集合（set）/ 被演算子（operand）	演算子（operator）
オブジェクト指向（Object-oriented programming）	オブジェクト（object）	メソッド（method）
圏論（Category theory）	対象（object）/ 圏（category）	射（morphism）

情報処理・プログラミング

データ（data）

処理（operation）

関数は、解析学として発展してきた歴史的な経緯から、集合に該当する概念を • 定義域（domain）• 値域（range） と表現することが多いです。おそらく義務教育ではこの路線で最初に学習させられたはずです。

https://www.mathsisfun.com/sets/domain-range-codomain.html

写像(関数) f の定義域/始域(domain)は X写像(関数) f の値域(range)は f(x)写像(関数) f の終域(codomain)は Y 定義域（Domain）

数学における写像の定義域（ていぎいき、英: domain of definition）あるいは始域（しいき、英: domain; 域, 領域[1]）とは、写像の値の定義される引数（「入力」）の取り得る値全体からなる集合である。つまり、写像はその定義域の各元に対して（「出力」としての）値を与える。

値域（Range）

数学、特に素朴集合論における写像の値域（ちいき、英: range）は、その写像の終域または像の何れかの意味で用いられる。現代的な用法ではほとんど全ての場合において「像」の意味である。 注意「値域」("range") は異なる意味で用いられうるから、教科書や論文を読む際にいずれの意味であるかを確かめるのは初手の演習として手頃であろう。古い本では「値域」を今日でいうところの終域の意味で用いている傾向がある[1][2]。より現代的な本では大半が今日でいう像の意味で用いる[3]。紛れを無くす目的で「値域」という語は用いないという本もある[4]。

終域（Codomain）

数学において写像の終域（しゅういき、英: codomain; 余域）あるいは終集合（しゅうしゅうごう、英: target set）は、写像を f: X → Y と表すときの集合 Y、すなわち写像 f の出力する値がその中に属するべきという制約を定める集合をいう。終域の代わりに「値域」という語を用いる場合もあるが、値域は写像の像（出力される値すべてからなる集合、f: X → Y で言えば f(X)）の意味で用いることが多いので注意すべきである。 定義と注意さて Bourbaki (1954) の意味で写像（函数）を定義するのであれば、終域は写像 f の一部として含まれる[1]。即ち、写像 f とは三つ組 (X, Y, F) であって F が直積集合 X × Y の函数的部分集合（すなわち函数関係）[2]かつ F に属する順序対の第一成分の成す集合（すなわち定義域）が X に一致するものをいう。このとき集合 F はこの写像のグラフと呼ばれる。また、x が写像 f の定義域 X の元を亙るとき、f(x) の形に書ける元全てからなる集合を f の値域と呼ぶ。一般に値域は終域の部分集合であって、従って一般には両者は一致しないことが起こり得る。一致する場合（すなわち全射）でないならば、終域に属する適当な元 y に対して、方程式 f(x) = y は解を持たない。 ブルバキはまた別な定義として、「写像」を単に函数的グラフそのものと定め[3]、これはまた広く用いられている定義である[4]が、これには終域が定義として含まれない。例えば集合論（英語版）において、定義域 X が真の類であることを許す方が望ましいという場合には、三つ組 (X, Y, F) といったものは厳密な意味では存在しないため定義に用いるには不適当だが、グラフによる定義ならば自然である。ただ、文献によっては f: X → Y という見かけ上終域に言及する形で写像を導入していながら、その後は暗黙にこの終域を含めない定義を用いる場合もあるので注意が必要である[5][6][7][8][9]。

もう数学用語としても値域と終域に至っては定義に「注意」とかあって地獄のような混乱ぶりです。しかし実際は、よほどのことがない限り関数型プログラミングでは、そこまで厳密になる必要はありません。型システムはおそらく、定義域/始域(domain)から推論される値域(range)＝f(x)を暗黙の終域(codomain)としているはずです。 こういう事情においてもプログラミング界隈では、ざっくり「型（type）」というたったひとつの言葉でまとめて表現して議論していて、プログラミング界隈での数学への意識の低さが適当に誤魔化されながら、あたかも厳密な定義をもとに運用しているようには見えることが再確認できます。 重要なのは、プログラマーは最低限、写像(関数) f の定義域/始域(domain)は Xという宣言くらいはしたほうが良いだろう、ということです。TypeScirptを含めて最近の型システムは優秀なので、かなりの精度で、値域(range)＝f(x)は暗黙の終域(codomain)として推論されるので、そこは原則放置していれば良いですし、うまく推論されていないな、という場合は、プログラマ自身が型アサーション(Type Assertion)で、終域(codomain)を決め打ち宣言してやれば良いでしょう。 たとえば、y = 2xという関数で、定義域すら定義していないとどういいうことになるか？というと 定義域が実数全体の場合

定義域が 0 ⩽ x ⩽2 の場合

定義域が自然数（x ⩾ 0）の場合

y = 2xという関数は定義域によってグラフは別物になっていますが、コード上ではまったく区別しない、ということになってしまいます。 以前はJavaScriptの制約により、TypeScriptでも整数（integer）型は存在しておらず、ざっくりNumber型しかなかったので、「関数の定義域や値域・終域は整数である」ということですら型システムで保証することができなかった、つまり、上記のグラフの関数は全部一緒くたの扱いという結構悲惨な状況でしたが、TypeScriptも普及している現代でこれはさすがにまずい、ということになったんでしょう、ES2020から整数を扱えるBigIntが導入されました。当然、関数（演算）の定義域からすると別物の形になるので、混ぜるな危険的なことが書かれています。

BigInt はいくつかの点で Number と似ていますが、重要ないくつかの点が異なります。組み込みの Math オブジェクト内のメソッドでは利用できず、演算で Number の値と混ぜることができません。同じ型に統一する必要があります。ただし、BigInt を Number へ変換する際には精度が落ちることがあるので、相互に変化する場合には注意が必要です。

定義域が 0 ⩽ x ⩽2 と書けるような、部分集合型をサポートしている型システムはあまり存在しないかもしれませんが、NumberあるいあBigIntから派生して user-defined type guardなどを利用することである程度は定義域がある独自の型を実現可能であると思われます。TypeScriptで他にやり方があるでしょうし（Coding Adventure: PositiveNumber in TypeScript）、本稿ではTypeScriptの個別の高度な機能の解説を目的としてはいないので、ここは踏み込みません。 可能な限り定義域についても、そして整数と実数の区別くらいはしたほうが良いですし、さすがにいくらなんでも数と文字列との区別くらいはしっかり区別しておかないとまずいでしょう、ということです。 これが型（Type）＝ 集合（Set）＝ 定義域（Domain）の重要性です。 12. 関数の表記法12.1. f(x) 記法とアロー記法 集合 X の各要素 x に集合 Y の1つの要素 y を対応させるXからYへの写像=関数

があるとき、• f(x)記法• アロー記法と2系統の記法が存在すると分類した上で、説明します。 12.2. プレースホルダ（placeholder）という概念下準備として、プレースホルダ（placeholder）という概念を確認しておかなければなりません。

プレースホルダとは、実際の内容を後から挿入するために、とりあえず仮に確保した場所のこと。また、そのことを示す標識などのこと。

プレースホルダのことは多分みんなよく知っていて、こういうやつです。

ここで、姓 名 ユーザー名 パスワードと仮の標識が入っていますね。「仮なんですよ？わかってますよね？？」ということをあえて示すためにたいていグレー色で仮っぽい雰囲気を醸し出しています。 英語のアカウント登録ならばもちろん

仮にこうなってるわけです。プレースホルダだという理解さえ共有されたら、字面なんてものは適当に何でも良いわけです。

上の図の集合 X の各要素 x に集合 Y の1つの要素 y を対応させるXからYへの写像=関数のうちxとyという小文字だけがプレースホルダです。 Googleアカウントの登録ならば、灰色の文字面がプレースホルダであるという共通の理解が、今どきのIT世界の住人の我々には広く教育されているわけですが、こういう数学のxとかyになると、まともに啓蒙される機会はほぼないので理解されておらず、おそらくほとんどの高校1年生は混乱しています。 この関数の概念図で、XとYは、なんらかの具体的な型（type）を意味して、その写像として f と具体名をつけたのですが、このxとyは、この概念図の関係性のなかで、各要素を抽象化した仮の名前であってプレースホルダです。 たとえば、国から都市へ対応させる首都関数の場合は、

ニューヨーク　ローマワシントンDC国都市首都集合(set)集合(set)　大阪　パリ　東京ロンドン　日本フランスアメリカイタリアイギリスｘcountyayb単に適当な文字の割当に過ぎず、集合である国、都市、そして関数名である首都という具体性な概念と名前と異なり、単にそれぞれの集合の一要素であるという属性に仮の名前をつけているだけのプレースホルダです。xでもaでも、あるいはもっと属性がわかりやすくcountryという名前のプレースホルダでも構いません。 countryであるとか、あるいはFirst nameとか書いていると、これは集合の名前を表しているのではないか？という捉え方もできますが、たしかに、後々わかりやすいように集合の名前そのままをプレースホルダとして使ったとしても別に構わないし、あるいは集合と関係ないxでもaでも構わない、どのようにしてもよい、そのシンボル自体にID的な機能などないというのがプレースホルダなのです。実際にたとえば、

となっている場合は、確認となっているプレースホルダであとで決まる値は、集合としてはもちろんパスワードとなるのですが、別に集合と一致させてパスワードとするよりあえて工夫した別の名前にしたほうがユーザにとってわかりやすい表示になるので、なんでもいいから確認という名前のプレースホルダにできているわけです。 12.3. f(x) 記法の関数の定義

中学数学では導入されませんが高校数学でまっさきに習う関数の記法です。これは実は、既に説明したとおり、関数をある単項演算子 f として扱った 表現にほかなりません。

単項演算（Unary operation） の場合 単項演算とは、数学で、被作用子（オペランド）が一つだけであるような演算（つまり、入力が一つの演算）のこと。たとえば、論理否定は真理値に対する単項演算であり、自乗は実数に対する単項演算である。階乗 n! も単項演算である。与えられた集合 S に対する単項演算は、関数 S→S に他ならない。 たとえば、論理否定の演算子 ! !true // false!false // true は、 const f = a => !a; f(true); // falsef(false); // true と関数表記へそのまま置き換えることができ、一項演算子は１引数の関数(Unary function)と対応するのがわかります。 !(true) // falsef(true) // false とすれば、単にシンボルの割当ての違いにすぎない、とはっきりとわかります。

さらに一般的な数学では、2つのある集合XとYのうちの要素であるxとyというプレースホルダを用意することで、y = f(x)と書くことができて、f の x における値が y であるという意味合いになり、xと y というプレースホルダを含む、なんらかの写像の対応法則 f であると明示できます。 コードではプレースホルダである y については言及することはなく、たとえば、f(x) = x + 1 のとき、

function f(x) { return x + 1; }

と書きます。これは、関数宣言

関数宣言 (関数文) は、指定された引数を使用して関数を定義します。

であり、文（statement）ですね。 数学で一般的に利用されているf(x)記法そのまま踏襲した感じではありますが、まずは文であることも災いして、簡潔ではなく、文字数も多く、たいへん打ちにくく読みにくいです。12.4. f(x) 記法の関数の適用関数を定義することを普通に、関数定義（function definition）と呼ぶとして、関数を使うことは、適用（application）、関数適用（function application）と呼びます。関数定義（function definition）とセットで使う言葉なので覚えておくと話が通じやすくなって便利です。 f(x) 記法の関数の適用をするときには、xがプレースホルダなので、そこに具体的な値を入力してやれば良いはずです。Googleアカウントの登録時のプレースホルダに具体的な値を入力するのと全く同じ作法であるとは言えます。

f(5) // 6f(10) // 11

ちなみにここで

関数型コードは値が変化するようなことはない let で定義した i x sum のようにコードの流れで値がコロコロと変化していくようなことはなく、const で定義するように値は定数として（一発で）定義されます。あとから値を二重に破壊的代入しようとするとエラーが出ます。 const x = 5;x = 10; // error 命令型では、 let x;x = 5;x = 10; というコードがJavaScriptでもちろん有効で、実際、 for (let i = 0; i < 10; i++) {//.... というように命令型コードのforループを回すときなどに必要になってくるのですが、関数型コードではアンチパターンです。理由はコードの位置、上下関係で値が変化すると式自体に明示されていない余剰の要素が紛れ込んで論理構成が破綻するからです。 関数型コードでは命令型コードのように命令文の上下の並びから発生するコードの流れ（フロー）をベースにするのではなく、式の構成によってプログラミングしていきます。

ということを再確認してください。 関数のパラメータである xはプレースホルダなので、あとから別の値を適用可能なのですが、関数のパラメータでもない通常の変数（関数型コードでは常に定数）はプレースホルダではありません。12.5. f(x) 記法でもアロー記法でもない関数の定義関数式

function キーワードは、式の中で関数を定義するために使用されます。

文（Statement）ではなく式（Expression）のバージョンの関数定義です。

const f = function (x) { return x;};

関数定義時に f(x) という字面はなくなり、fという関数名で新しい関数を定義している、ということが明示的になりました。同時に、xはプレースホルダとして右辺へと分離されたことも進歩ではあるでしょう。 しかし、the中途半端で、式とは言いつつも、関数文を入れ替えただけで冗長さはそのまま残っており、だらだらと長く読みづらいです。 12.6. アロー記法の関数の定義

アロー関数式です。もちろん文ではなく式であり、プログラミング界隈ではラムダ式という名称のほうが有名で通用しやすいはずです。 簡潔で美しいですね。無駄を取り去った機能美です。

xとyはプレースホルダであることを考慮して、x が x + 1 に写像される、というイメージそのままになっています。

二項演算子（Binary operator）はとてつもなく強力な記法である まったく同じ意味のコードであっても、べき乗 (**)という新しい二項演算子を導入した結果、いかにコードが無駄なく簡潔になり、数学的な構造が読みやすくなったのかは明白です。 特にこのように連鎖してネスト構造になった場合、非常にシンプルに記述できます。これはバグの混入を事前に防ぐことができ、プログラミングの生産効率が飛躍的に向上することに直結します。 二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y) のことであり、概念としては、関数だけで統合できてしまうのですが、数式の表記方法としてはむしろ、x ◦ y のほうが圧倒的に優れており、なにより、これは繰り返しになりますが我々が小学校の算数の時間から徹底的にトレーニングされてきた慣れ親しんでいる表記でもあります。非常に直感的に理解可能です。

というのと全く同じ原理で、簡潔で美しい本質的なイメージを表現した記法というのは大変強力なのです。 ラムダ式（アロー関数式）は写像を表現するプレースホルダだけで構成されています。

そして、この x というのはあくまでプレースホルダにすぎないので、

別のシンボルたとえば a であっても全く同じ意味になります。 そして、その上でここには、プレースホルダではない、意味がちゃんとある名前である関数名の f はありません。関数に名前をつける、という行為はまた別の概念だからですね。別の概念ならば一緒くたにせずに、表記としてもしっかり分離したほうが、このようにプレースホルダのシンボルなんだから別のシンボルでも構わない、であるとか、関数名はプレースホルダではないので命名には特段の意味がある、という概念の混同が発生していません。それに関連もしますが、概念の粒度が小さいので混乱もないし構成の自由度で優れています。こちらの表記のほうが概念的にミニマルでコンパクトで、写像（Map）の概念そのままのイメージ的に自然なのですが、あまりにも、f(x) という関数名とプレースホルダは同時にセットで定義する、混沌とした数学の流儀が当たり前に数学世界とプログラミング世界に浸透しているため、ラムダ式は無名関数という奇妙なネーミングさえあります。 もし関数名が必要なのであれば、単純に、

というように関数名 f を別途割り当てて定義すれば良いだけです。 アロー関数式には、 関数で非常に扱いづらいthisをはじめとするオブジェクト指向、それから命令型の、まさに関数型コードの式とは相容れないキーワードがズラリと並んでいます。これらは関数型では脱却すべきアンチパターンということになり、むしろ制限がかかっているほうがアンチパターンを関数型プログラマが不用意に書くことを未然に防止してくれるので歓迎すべきことです。 本稿において、すでにfunction thisは利用しました。 Arrayオブジェクト に+ という記号のプロパティでArray.concat() というメソッドを拡張してしまいます。

Object.defineProperty( Array.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this.concat(R); // `this` is Left hand side of the Binary operator }});

このコードでは、this.concat(R) と単純にArrayオブジェクトメソッドを + というオブジェクトプロパティにコピーしています。その結果、

array1.concat(array2);array1['+'](array2);

となります。 二項演算子であるカスタムオペレータを定義する際に、JavaScriptのArrayオブジェクトをthisで自己参照して、それを左辺のオペランド（被演算子）にする必要があったからです。 このようにオブジェクト指向のメソッドを関数型の二項演算子として置き換えるという、ハックコードのときだけオブジェクト指向のコードを触るので必然的に例外的にラムダ式以外の関数定義をします。逆にそこ集約されてそれ以降は一切オブジェクト指向のコードやthisを書く必要はなくなります。 12.7. アロー記法の関数の適用

慣れ親しんでいる単項演算子であるf(x) という関数定義には、xというプレースホルダがセット組み込まれていて、関数適用の際にはプレースホルダを具体的な値で置き換える、という自然で合理的な作法ですが、問題があります。 アロー記法のラムダ式の定義は、プレースホルダだけで構成されており、関数名 f は独立して扱われています。関数の適用についても、関数名とプレースホルダが渾然一体となった f(x) 記法を踏襲しなければいけない理由はない気がします。 関数の定義の表記法としてアロー記法は機能美があり優れていました。アロー記法の関数適用というのはないのでしょうか？ 13. f(x) 記法からの脱却　パイプライン演算子（Pipeline Operator） 13.1. f(x) 記法の問題点

慣れ親しんでいる単項演算子であるf(x) という関数定義には、2つ問題があります。 • ネスト地獄• 同一の()というシンボルで、異なる意味の機能 f(x)表記方では、データの流れの左右が逆になってしまう入れ子（nesting）構造つまり x を f 次に g 次に h に適用という概念がh(g(f(x)))となっており、「まあいいじゃないか、数学でもそういう記法が普通なんだし・・・」と甘くみていると、

べき乗 (**)という二項演算子がES2016で導入されました。 Math.pow(2, 3) ==2 ** 3 Math.pow(Math.pow(2, 3), 5) == 2 ** 3 ** 5 これは、まさに、二項関数（Binary function）Math.pow(x, y)を二項演算（Binary operattion）x ** yへ置き換えたものです。

というように、関数適用が連続的になると、入れ子構造が発生して、コードのリーダビリティが損なわれてしまいます。コードの構造が読み取りにくくなるので非常にデバッグしにくなります。二項演算では左右のパイプで簡潔に表現され理解もできるものが、入れ子（nesting）構造となり地獄のような有様になります。 これは根本的には、単項演算子としてのf(x)表記法に不合理なレベルで執着し続けてきた悪しき帰結であると言えます。

単項演算（Unary operation） の場合 単項演算とは、数学で、被作用子（オペランド）が一つだけであるような演算（つまり、入力が一つの演算）のこと。たとえば、論理否定は真理値に対する単項演算であり、自乗は実数に対する単項演算である。階乗 n! も単項演算である。与えられた集合 S に対する単項演算は、関数 S→S に他ならない。 たとえば、論理否定の演算子 ! !true // false!false // true は、 const f = a => !a; f(true); // falsef(false); // true と関数表記へそのまま置き換えることができ、一項演算子は１引数の関数(Unary function)と対応するのがわかります。 !(true) // falsef(true) // false とすれば、単にシンボルの割当ての違いにすぎない、とはっきりとわかります。

シンボルの割当てといえば、2つ目の問題もあります。 演算子とともにグループ化演算子 ( ) を組み合わせることで依存グラフを構成し、演算はその依存グラフを解決する形で進んでいきます。とするわけですが、 • f(x) という単項演算子としての記法のカッコ（）• グループ化演算子 ( ) のカッコ（） は、異なる概念の機能を同一のシンボル( )で表現しています。意味が異なる同じ記号が入れ子を繰り返しながら式の依存グラフを構成していくので、読解は非常厄介なコードになってしまいます。 コードというより、これはベースとなる数学の「ミス」とも言えて、おそらくこれも手書き時代にオイラーが発明した記法でしょうが、概念が別ものならば、本来ならば別のシンボル<> [] で表しても良かったのでしょうが、この具体的なシンボルでも重複はするので問題があります。 　 関数型言語のHaskellではf(x) はf x と書けて、たいがいのコードでは（）なしの関数適用の表記がなされています。筆者は最初、なんでこんな（JavaScriptやC系のプログラマにとって）わかりにくい記法なのだろうか？と謎だったのですが、上述のような（）の概念の混同や、とにかく関数型コードでは（）だらけになって大変なことや、さらに後述するカリー化で、2引数の関数f(x, y) は１引数の関数(Unary function)の高階関数として表すので、f(x)(y)となりますが、（）を書かないことで、f x y となり、カリー化した１引数の関数(Unary function)の高階関数と2引数関数の表記差異がなくなる、などとメリットはあります。 一般的な数学でも、高校数学では、三角関数でも、sin(x)と表記する煩雑さを嫌って、sin xと書く流儀と一緒で、関数適用まで()を使うのは混乱するし煩雑で面倒だから避ける、という流儀は存在しています。 この無用に複雑で意味さえ異なる（）の入れ子構造を生み出し続けるf(x)記法以外の関数適用の記法はないでしょうか？ 13.2. データファーストになるパイプ構造 f(x)とあるとき、データは x のほうなのでデータファーストにするならば f よりむしろ x のほうが最初に来るべきです。我々はデータである x と関数である f の関係を今一度とらえなおして、単項演算の表記に執着するのではなく、二項演算にしたほうが良いでしょう。

関数適用を二項演算と見做したときの二項演算子がパイプライン演算子（Pipe Operator）です。データファーストのパイプラインを実現するための二項演算子なので、自然な呼称です。たとえば、f(x) 記法では　g(f(x))とネストしてしまっているものは、パイプライン記法で、x |> f |> g と表現できます。

赤の波線が出ているのは、JavaScriptでもTypeScriptでも実装されていないからですね。パイプライン演算子

パイプライン演算子（パイプラインえんざんし、英語: Pipe Operator）(|>)は、ある式の結果を別の式に1つ目の引数として渡す演算子である。主に、関数の引数に他の関数を書くことにネストが深くなり、コードが読みにくくなるのを防ぐためにある。Elixir、F#、R言語などにある。

関数型プログラミングは式（Expression）を組み立てていく作業に他なりません。前述したとおり、

オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数は、二項演算の右側の被演算子（Operand）になります。 また、オブジェクトのメソッドチェーンは、二項演算の連鎖と同じものである、という事実を認識できるでしょう。

オブジェクトのメソッドチェーンは、二項演算の連鎖と同じという事実は、別の言葉でいうと、データファーストのパイプ構造になっている、ということです。二項演算では、小学校の算数の授業で習ったとおりに、左から右に演算が進んで行く作法で、それはこういう文章の読解が左から右である事実とも一致しますし、データが左から右に、上から下へと流れていくというのはすべてにおいて自然です。 データファーストのパイプ構造である二項演算は非常にわかりやすく、メンタルの負荷を劇的に軽減させ無用なミスを減らしBUGがなくなるのでコーディングの生産性を劇的にあげることができます。 その証拠というか、実際にこのパイプラインオペレータがもたらすであろうメリットはJavaScriptコミュニティでは広く認識されているようで、#StateOfJS 2020: What do you feel is currently missing from JavaScript?2020サーベイ:JavaScriptに欠けていると感じるものは？では、

Pipe OperatorはPattern Machingに次ぐ第４位となっており、現在のJavaScriptプログラマーにとって特段に需要が高い機能であることが確認できます。 13.3. 独自のパイプライン演算子をJavaScriptで実装する試み上記2020サーベイの第3位であるパターンマッチングの余談でも論じましたが、TC39による標準的な実装というのは迷走しておりけしてアテにしてはいけないので、自前で実装するしかありません。 パターンマッチングの著名ライブラリであるts-patternでは、

パターンマッチングは、Haskell、Rust、Swift、Elixir、その他多くの言語で実装されています。EcmaScript仕様にパターンマッチングを追加するためのtc39プロポーザルがありますが、まだステージ1であり、この先数年は実装されそうにありません（仮に実装されることがあったとしても）。幸運なことに、パターンマッチングはユーザーランドで実装することができます。 ts-patternは、タイプセーフなパターンマッチングの実装を提供しており、今日から使い始めることができます。

とユーザランドで実装することが容易であることが書かれていますが、関数適用の演算子などというJavaScriptのすべての値に深いれベルでコミットする二項演算子を実装するのは工夫が必要です。 実際の実装、コードについては後回しにします。現在の説明の到達点ではコードの解説のオーバーヘッドが大きすぎるからです。パイプライン演算子はすでに実装できた、ということで話をすすめます。　13.4. 関数（写像）の連鎖をイメージ通りに表現できるパイプライン演算子この項目は、あとから出てくる説明のコピペです。構成の都合上「関数（写像）の連鎖と関数（写像）の合成」これも少し後回しにしているのですが、パイプライン演算子の実装が、現時点では混乱を招く、というのと逆に、コピペの箇所に限っては現段階の知識レベルですんなりと理解できます。そしてその内容こそが、パイプライン演算子を導入したい動機であり、実際の使い方もわかります。

関数（写像）の連鎖と関数（写像）の合成（Function composition） 関数（写像）の連鎖 という写像は、アロー関数式で、 というように関数 f が定義する表現ができますが、写像を連鎖させることができます。 346ABC+1+2+3346+1+2+3 const f = x => x + 1;const g = x => x + 2; とすると、fx表記法では、 g(f(3)); // 6 となります。入れ子構造になっており写像のイメージで直感的ではないので、独自に実装した、パイプライン演算子（Pipeline Operator）を活用して、 P(3)['>'](f)['>'](g)　　// 6 と表現できます。

13.5. 二項演算子で式を書けばコードはシンプルになりType定義の構造と一致しやすい 以下は、本稿の最後のほうで出てくる、関数型プログラミングを机上の空論で終わらすことなく、リアルに実用的である為に欠かすことができない、FRP（Functional Reactive Programming）関数を定義するコード（タイプコンストラクタ）なのなのですが、これはオブジェクト指向プログラミングにおけるクラスのコンストラクタに該当します。

オブジェクト指向や命令型の幾多のキーワードの文（Statement）を一切つかうことはなく、型（type）定義を別にすると、単に、関数と二項演算子のみで構成した単一の式（Expression）でしかありません。もちろんreactiveやflatReactiveという名前の関数は見えるのですが、それは別の所で定義されていて、この単一の式の構造こそがこのFRP関数の概略の表現なのです。 実際にこの式の構造は、それ自体そのまま、完全にTypeScriptの型（type）定義と一致しています。 • TypeScriptの交差型(Intersection Types)の & • 独自に定義した二項演算子（Custom operator）であるパイプラインオペレータ（Pipeline Operator）の ['>'] それらがうまく呼応しており、簡潔なコードとして表現できていることに注目してください。 TypeScriptでコーディングするときには、コードがオブジェクト指向のスタイルであろうと関数型のスタイルであろうと、最終的に、あるいは最初から決まる型（Type）は同一でしょう。そして関数型のコードでは特に二項演算子を活用する式を構成すれば、自動的にTypeScriptの型定義と一致するコードになります。

二項演算子（Binary operator）はオブジェクト指向のコードを置き換え可能な、強力な表記法

を体現するものと言えます、 二項演算子（Custom operator）を適切に定義しながら活用することで、構造が明確なコードが表現できるようになり、結果的に自然とTypeScriptによる型定義とも簡単に対応させやすくなり、より厳密な型構造を維持するBUGのないコードを書けるようになります。 13.6. 二項演算子（Custom operator）は見やすくて書きやすい まず、大変重要なことですが、TypeScriptで普通にタイプが効きます。連想配列表記のメソッドになっているから、型推論が破綻する、ということはありません。 次に見た目ですが、 次に、最初見た目やっぱり煩雑だな、と思っていたのですが、VSCode　August 2021 (version 1.60)Built-in fast bracket colorizationBracket pair colorization 10,000x faster昔は、外部エクステンションであったブラケットの色付け機能が最近VSCode組み込み機能となりました。組み込みですがデフォルトでは有効ではないので設定する必要があります。

ブラケットの色付けにより、CustomOperatorの[ ]が式の階層によって正確に色分けされるようになりました。 たとえば、JavaScriptに最初から実装されている二項演算子たとえば + などでは

と、どの式の階層でも同じ色なのですが、Custom operatorを使ったコードでは、

というように式の階層によって自動的に色分けがなされるので非常に見やすいです。

特に筆者が利用しているテーマ　Monokai Proでは、二項演算子は黄色で目立ってわかりやすいです。同じ色の演算子でもブラケット[]がトップレベルでは紫ですが、一段階層が下がると青になっているのがひと目で判別できます。　書きにくさの問題が懸念されるところですが、User SnippetsあるいはKeyboard Shorcutsを活用することでその問題はなくなります。

[ { "key": "F1", "command": "editor.action.insertSnippet", "args": { "snippet": " => " } }, { "key": "F2", "command": "editor.action.insertSnippet", "args": { "snippet": "['>'](" } },]

デフォルトのままだと気になるレベルですが、VSCodeにあらかじめ搭載されている機能を活用することで、独自に定義した二項演算子（Custom operator）は、読みやすく書きやすいものとなります。　14. 代数構造（代数的構造）（Algebraic structure）と有向非巡回グラフ（DAG）＝依存グラフ14.1. これまでのまとめ関数型コードは式（Expression）である。関数型プログラミングは式を組み立てていく作業。式の中心となる素材が、関数（Function）と二項演算子（Binary operator）。関数（Function）と演算子（Operator）は本当は同じもの。

二項演算子（Binary operator）はとてつもなく強力な記法であるまったく同じ意味のコードであっても、べき乗 (**)という新しい二項演算子を導入した結果、いかにコードが無駄なく簡潔になり、数学的な構造が読みやすくなったのかは明白です。特にこのように連鎖してネスト構造になった場合、非常にシンプルに記述できます。これはバグの混入を事前に防ぐことができ、プログラミングの生産効率が飛躍的に向上することに直結します。二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y) のことであり、概念としては、関数だけで統合できてしまうのですが、数式の表記方法としてはむしろ、x ◦ y のほうが圧倒的に優れており、なにより、これは繰り返しになりますが我々が小学校の算数の時間から徹底的にトレーニングされてきた慣れ親しんでいる表記でもあります。非常に直感的に理解可能です。

関数型のコードでは、二項演算子とともにグループ化演算子 ( ) を組み合わせることで依存グラフを構成し、演算はその依存グラフを解決する形で進んでいく。依存グラフを構成する二項演算を最大限に活用した式の組み立てに注力することで、バグの入り込む余地が極小の関数型コードを書くことが実現できる。型（Type）とは集合（Set）のこと。オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数は、二項演算の右側の被演算子（Operand）。

型理論（Type theory）	型（type）	関数（function）/ 写像（map）
集合論（Set theory）	集合（set）始集合（domain）と終集合（codomain）	写像（map）
解析学（Analysis）	定義域（domain）と値域（range）と終域（codomain）	関数（function）
代数学（Algebra）	集合（set）/ 被演算子（operand）	演算子（operator）
オブジェクト指向（Object-oriented programming）	オブジェクト（object）	メソッド（method）
圏論（Category theory）	対象（object）/ 圏（category）	射（morphism）

情報処理・プログラミング

データ（data）

処理（operation）

このなかで、最も根底となる、すべての概念の包括的な枠組みが圏論（Category theory）で、これまで永らく数学の基礎であった集合論でさえも圏論の言葉で再定義されます（集合の圏（category of sets）における射（morphism）は関数（function）になる）。本稿の方針は、二項演算子(Binary operatior)を最大限に活用することなので、このなかでどの分野の言葉をもってコードを書いていくのか？となると、当然、代数学（Algebra）。関数適用のf(x)記法からの脱却をし二項演算子であるパイプライン演算子にしていく。ソフトウェア開発、あるいはプログラミングにおける「本質的な複雑性」（essential complexity）とは、ほんとうは数学的な概念で、それは、組合せ爆発（Combinatorial explosion）。『銀の弾丸』、複雑性を解決する唯一の「唯一正しい工学的アプローチ」とは「数学的アプローチ」でしかありえず、組合せ爆発を回避する「等しい（Equality）」という超強力な概念。 14.2. Twitterは代数構造と有向非巡回グラフ（DAG）＝依存グラフを活用して自社システムを組んでいるいろんなSNSプラットフォームがありますが、個人的な印象ではTwitterの技術水準が格段に高いと評価しています。 https://github.com/twitter/algebirdhttps://twitter.github.io/algebird/

Algebird is a library which provides abstractions for abstract algebra in the Scala programming language.This code is targeted at building aggregation systems (via Scalding, Apache Storm or Summingbird). It was originally developed as part of Scalding’s Matrix API, where Matrices had values which are elements of Monoids, Groups, or Rings. Subsequently, it was clear that the code had broader application within Scalding and on other projects within Twitter. Algebirdは、Scalaプログラミング言語で抽象代数のための抽象化を提供するライブラリです。このコードは、(Scalding, Apache Storm, Summingbirdを介した)アグリゲーションシステムの構築を対象としています。元々はScaldingのMatrix APIの一部として開発されたもので、Matrixはモノイド、群、環（Monoids、Group、Ring）の要素である値を持っていました。その後、このコードがScaldingやTwitterの他のプロジェクトで、より幅広い用途に使えることが明らかになりました。

Apache Storm

Apache Storm is a distributed stream processing computation framework written predominantly in the Clojure programming language. Originally created by Nathan Marz[1] and team at BackType,[2] the project was open sourced after being acquired by Twitter.[3] It uses custom created "spouts" and "bolts" to define information sources and manipulations to allow batch, distributed processing of streaming data. The initial release was on 17 September 2011.[4]A Storm application is designed as a "topology" in the shape of a directed acyclic graph (DAG) with spouts and bolts acting as the graph vertices. Edges on the graph are named streams and direct data from one node to another. Together, the topology acts as a data transformation pipeline. At a superficial level the general topology structure is similar to a MapReduce job, with the main difference being that data is processed in real time as opposed to in individual batches. Additionally, Storm topologies run indefinitely until killed, while a MapReduce job DAG must eventually end.[5]Storm became an Apache Top-Level Project in September 2014[6] and was previously in incubation since September 2013.[7][8] Apache Stormは、主にClojureプログラミング言語で記述された分散型ストリーム処理計算フレームワークです。元々はBackType社のNathan Marz[1]とそのチームによって作成されたが[2]、Twitter社に買収された後にオープンソース化された。[3]カスタムで作成された「spout」と「bolt」を使用して情報源と操作を定義し、ストリーミングデータのバッチ分散処理を可能にしている。2011年9月17日に最初のリリースが行われた[4]。Stormアプリケーションは、有向非巡回グラフ（DAG）の形をした「トポロジー」として設計されており、スパウトとボルトはグラフの頂点として機能します。グラフ上のエッジはストリームと呼ばれ、あるノードから別のノードへデータを転送します。これらのトポロジーは、データ変換のパイプラインとして機能します。一般的なトポロジーの構造は、表面的にはMapReduceジョブに似ていますが、主な違いは、データが個々のバッチではなく、リアルタイムで処理されることです。さらに、MapReduceジョブのDAGが最終的に終了しなければならないのに対し、Stormのトポロジーはキルされるまで無限に実行される[5]。Stormは2014年9月にApache Top-Level Projectとなったが[6]、それ以前は2013年9月からインキュベーション中であった[7][8]。

有向非巡回グラフ（DAG）という依存グラフ構造の構成のことを、Apache Stormでは「トポロジー」と表現しており、実際そのとおりなのですが、別にトポロジーのことは、少なくともこの程度のレベルでは代数構造に統合して考えられるし、必要以上に概念や用語を積み増すことは無用な混乱につながるだけなので、代数構造と、表裏一体である、依存グラフ、という概念に統合して考えていきます。 14.3. 代数構造（代数的構造）（Algebraic structure）代数的構造

数学において代数的構造（だいすうてきこうぞう、algebraic structure）とは、集合に定まっている算法（演算ともいう）や作用によって決まる構造のことである。代数的構造の概念は、数学全体を少数の概念のみを用いて見通しよく記述するためにブルバキによって導入された。また、代数的構造を持つ集合は代数系（だいすうけい、algebraic system）であるといわれる。すなわち、代数系というのは、集合 A とそこでの算法（演算の規則）の族 R の組 (A, R) のことを指す。逆に、具体的なさまざまな代数系から、それらが共通してもつ原理的な性質を抽出して抽象化・公理化したものが、代数的構造と呼ばれるのである。なお、分野（あるいは人）によっては代数系そのもの、あるいは代数系のもつ算法族のことを代数的構造とよぶこともあるようである。 後者は、代数系の代数構造とも呼ばれる。現代では、代数学とは代数系を研究する学問のことであると捉えられている。

代数的構造の概念は、数学全体を少数の概念のみを用いて見通しよく記述するため

これが、関数型プログラミングで「代数構造」という概念をわざわざ持ち出してくるメリット、モティベーションのすべてです。 既に何度も強調しているとおり、二項演算子は根本的は二項関数でしかないのですが、

二項演算子（Binary operator）はとてつもなく強力な記法であるまったく同じ意味のコードであっても、べき乗 (**)という新しい二項演算子を導入した結果、いかにコードが無駄なく簡潔になり、数学的な構造が読みやすくなったのかは明白です。特にこのように連鎖してネスト構造になった場合、非常にシンプルに記述できます。これはバグの混入を事前に防ぐことができ、プログラミングの生産効率が飛躍的に向上することに直結します。二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y) のことであり、概念としては、関数だけで統合できてしまうのですが、数式の表記方法としてはむしろ、x ◦ y のほうが圧倒的に優れており、なにより、これは繰り返しになりますが我々が小学校の算数の時間から徹底的にトレーニングされてきた慣れ親しんでいる表記でもあります。非常に直感的に理解可能です。

要するに、関数そのもので議論したりコードに書き込むよりも、二項演算として表記したほうが圧倒的にコードが簡単になり、直感的に理解が可能で、見通しがよくなりメンテナンスが楽になる、つまりバグが紛れ込むリスクが激減するというとてつもないメリットがあるので、二項演算のほうを採用したい、そして、関数型プログラミングでは、二つの演算によって決まる代数的構造、つまり二項演算だけで、ほぼほぼ事が足りてしまうのです。 代数構造というのは代数学（Algebra）という学問で研究しつくされていて、

といろいろあるのですが、このリストのなかで関数型コードの基礎レベルあるいは、たいていのプログラミング要素をカバーできる特に有用な養素は、

この辺です。 14.4. ３つの代数構造と「等しい（Equality）」という概念「法則」であるとか「律」と書いていると面倒くさいことになった、と感じがちでなのですが、これこそが「等しい（Equality）」という超強力な概念のことなのです。 ソフトウェア危機＝「本質的な複雑性」（essential complexity）＝組合せ爆発を回避する「等しい（Equality）」という超強力な概念が体系的に整理されています。 いろんな代数構造が体系的に分類されているのですが、そのそれぞれにおいて、何かが「等しい（Equality）」という条件で絞り込みがなされています。 本稿で気にする、扱うのはせいぜい、結合性と単位元という２つの要素だけで、双方とも、何かが「等しい（Equality）」というルールです。 そして本稿で具体的に扱うのは 1. モノイド（Monoid）2. ファンクタ（Functor）3. モナド（Monad） 以上の、3つの代数構造だけで、これら3つともすべて二項演算の名前です。おおよそこれだけで、有向非巡回グラフ（DAG）による関数型リアクティブプログラミング（FunctionalReactiveProgramming）FRPまでカバーし、最終的には具体的なコードも示します。 15. モノイド（Monoid）複雑性を排除してくれるシンプルな二項演算 15.1. モノイド（Monoid）の具体例 モノイドとは以下のような二項演算で表現される代数構造です。 (1 + 2) + 3 = 1 + (2 + 3)(1 × 2) × 3 = 1 × (2 × 3) 式をコードで書くと、

(1 + 2) + 3 === 1 + (2 + 3); // true(1 * 2) * 3 === 1 * (2 * 3); // true ("Hello" + " ") + "world" === "Hello" + (" " + "world"); // true ([1].concat([2])).concat([3]) // [1,2,3] [1].concat([2].concat([3])) // [1,2,3]

最後のArray.concat()については、すでに独自の二項演算子のくだりで取り上げたので問題はないと思います。 15.2. モノイド（Monoid）の定義モノイド（Monoid）

数学、とくに抽象代数学における単系（たんけい、英: monoid; モノイド）はひとつの二項演算と単位元をもつ代数的構造である。モノイドは単位元をもつ半群（単位的半群）であるので、半群論の研究対象の範疇に属する。モノイドの概念は数学のさまざまな分野に現れる。たとえば、モノイドはそれ自身が「ただひとつの対象をもつ圏」と見ることができ、したがって「集合上の写像とその合成」といった概念を捉えたものと考えることもできる。モノイドの概念は計算機科学の分野でも、その基礎付けや実用プログラミングの両面で広く用いられる。 定義集合 S とその上の二項演算 •: S × S → S が与えられ、以下の条件結合法則S の任意の元 a, b, c に対して、(a • b) • c = a • (b • c).単位元の存在S の元 e が存在して、S の任意の元 a に対して e • a = a • e = a.を満たすならば、組 (S, •, e) をモノイドという。まぎれの虞のない場合、対 (S, •) あるいは単に S のみでも表す。 二項演算の結果 a • b を a と b の積[注釈 1]と呼ぶ。手短に述べれば、モノイドとは単位元を持つ半群のことである。モノイドに各元の可逆性を課せば、群が得られる。逆に任意の群はモノイドである。二項演算の記号は省略されることが多く、たとえば先ほどの公理に現れる等式は (ab)c = a(bc), ea = ae = a と書かれる。本項でも明示する理由がない限り二項演算の記号を省略する。

先に、モノイドの具体例を示しており、小学校の算数の時間に習った加法と乗法の二項演算であったり、JavaScript文字列（Strings）の結合とか、お馴染みの概念であるわけですが、以上が厳密な定義です。定義を見ると3つの要素があります。 1. 集合 S とその上の二項演算 •: S × S → S 2. 結合法則（結合律）3. 単位元の存在 15.3. モノイドの素晴らしさ①　型（Type）が単一の閉じた二項演算mono- というのはモノトーンという言葉などがありますが「単一」という意味がある接頭語です。日本語でも、単系（たんけい、英: monoid; モノイド）と和訳されているようですが、あまり使わず、カタカナのモノイドです。なにが単一（モノ）なのか？というと、型（Type）が単一で、それが、S × S → Sという式で表されています。 (1 + 2) + 3 = 1 + (2 + 3)(1 × 2) × 3 = 1 × (2 × 3)で言えば、Number × Number → Number文字列結合なら、String + String → String配列結合なら、　Array concat Array → Array と扱う型（＝集合 S）が１つだけで閉じた演算です。つまり、すべて「等しい」わけです。

『銀の弾丸』等しくすれば組合せ爆発（Combinatorial explosion）を回避可能 『銀の弾などない』（No Silver Bullet ）というのは誤りで、『銀の弾』は実は存在していて、それは「等しい（Equality）」という超強力な概念に他なりません。ソフトウェア開発、あるいはプログラミングにおける「本質的な複雑性」（essential complexity）とは、ほんとうは数学的な概念で、それは、組合せ爆発（Combinatorial explosion）です。 組合せ爆発（くみあわせばくはつ、英: combinatorial explosion）は、計算機科学、応用数学、情報工学、人工知能などの分野では、解が組合せ（combination）的な条件で定義される離散最適化問題で、問題の大きさn に対して解の数が指数関数や階乗などのオーダーで急激に大きくなってしまうために、有限時間で解あるいは最適解を発見することが困難になることをいう。 念の為ですが、解決したい課題の対象が本質的に原理的に内在している組み合わせ爆発のことではなく、プログラマが書いてしまいがちで、不注意な、あるいは、不適切な工学的アプローチによるコード自体が本質的には回避可能であるのにもかかわらず、非合理的に、無用に、組みわせ爆発を起こしている、ということです。無用な組合せ爆発を回避するためには、可能な限り要素を減らすこと、そして何より肝要なことは、本質的に等しいものは、等しいものとして徹底的に扱うこと、さらに必ずしも等しくなければならない要請はなくても、等しいものとして扱うことができるならば等しくする、ということです。要素が1つしかなければ、組み合わせというのが原理的に存在しないので、組合せ爆発による問題など起こりようがありません。しかし、それぞれの要素に区別があるときは、指数関数的に組み合わせ爆発が起こり収集はつかなくなります。数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないのですが、裏を返すと「唯一正しい工学的アプローチ」『銀の弾丸』とは、組合せ爆発を回避する「等しくする」という数学的アプローチです。

モノイドはまさに要素が1つしかなければ、組み合わせというのが原理的に存在しないパターンに該当していて、本質的な複雑性である組合せ爆発を回避できる非常に安全な代数構造です。 モノイドは工学的な観点からみると、工業規格と同じです。

数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないのですが、裏を返すと「唯一正しい工学的アプローチ」『銀の弾丸』とは、組合せ爆発を回避する「等しくする」という数学的アプローチです。実際これはソフトウェア開発に限らない一般的な工学的な問題として死活問題なので、工業規格という人類の経験則による知見が存在しています。ISO規格（国際標準化機構）があり、JIS（日本）など各国に規格が決定されています。 身近なところでは、電気のコンセントプラグがあり、特にプログラマにとっては、USB規格があります。 ユニバーサル・シリアル・バス（英: Universal Serial Bus、略称：USB、ユーエスビー）は、コンピュータ等の情報機器に周辺機器を接続するためのシリアルバス規格の1つ。ユニバーサル（汎用）の名の示す通り、ホスト機器にさまざまな周辺機器を接続するためのペリフェラルバス規格であり、最初の規格となるUSB 1.0は1996年に登場した。現在のパーソナルコンピュータ周辺機器において、最も普及した汎用インターフェース規格である。 もちろん、Appleのように独自の規格、つまり自前機器のエコだけで完結すれば良いだろう、というのもひとつの主張ではありますが、最近排除されて消費者に歓迎された事案は記憶に新しいところです。EU スマートフォンの充電器をUSB Type-Cへ統一へ（iPhoneのLightningケーブル排除へ） USBなどを使っているとわかりますが、こういう「等しさ」が担保されている概念はBuilding blockになります。その定められた規格内に収まってさえおれば、それらは「等しい」と見做され、自由自在に組み合わせても壊れる心配がありません。LEGOもそれ自体がBuilding blockであり単一の接続規格で、自由自在に構築可能です。 根源的には、コードの要素を等しく保つというアプローチで、コードをUSBデバイスやLEGOブロックのように自由自在に組み合わせてもコードは壊れないと担保される、バグのでないメンテナンス性の高いコードをプログラミング可能となります。

15.4. モノイドの素晴らしさ②　組み合わせ方に依存しない、結合法則（Associativity）組合せ爆発を回避できる非常に安全な代数構造であるためにもうひとつ肝要なことは、組み合わせの順序に依存しない、組み合わせの順序が異なっても「等しい」という性質です。 (1 + 2) + 3 = 1 + (2 + 3)(1 × 2) × 3 = 1 × (2 × 3) これは、型（Type）が単一、S × S → S にさらに上乗せした性質（法則）であることに留意してください。組み合わせの順序が異なっても「等しい」という性質のことを、結合法則（結合律、結合性）（Associativity）と呼びます。

数学における結合性（けつごうせい、英: associative property[1], associativity）は、一部の二項演算が持つ性質である。演算が結合的であるために満たされるべき条件を結合法則（けつごうほうそく、英: associative law; 結合律、結合則）という。 S の各元 a, b, c に対して、等式 (a • b) • c = a • (b • c) が満たされる。 ひとつの式の中に同じ結合的演算が一度に複数現れる場合、それらの演算を施す順番は、被演算子の並びの順を変えない限りにおいて、結果に影響を与えない。つまり、（必要ならば中置記法と括弧を使った式に書き換えて）そのような式における括弧の位置を入れ替えても、式の値は変わることはない。

USB機器やLEGOブロックも結合法則を満たしていて、つまり結合性があって、パーツの組み合わせ順序に依存しません。どのように組み立てを構成していっても結果は同じになるはずです。 逆に、もしUSB機器やLEGOブロックで、組み合わせ順序によって結果が異なる、ということになれば、非常に面倒くさく扱うのにかなりの注意が必要な代物になることは想像に難くありません。組合せ爆発が起こるからですね。 世の中には、構成の順序こそが重要という工業製品などはいくらでもありますが、プログラミングにおいては、なるだけ、構成順序に依存せず結果が等しくなる結合法則を満たすモノイドを選ぶべきです。 (1 + 2) + 3 = 1 + (2 + 3)(1 × 2) × 3 = 1 × (2 × 3) という加法と乗法の演算は結合性がありますが、同じ四則演算でも減法と除法は結合性がなく、モノイドではありません。 (3 - 2) - 1 ≠ 3 - (2 - 1)(4 ÷ 2) ÷ 2 ≠ 4 ÷ (2 ÷ 2) つまり、引き算、割り算の演算をコードに安易に組み込んでしまうと、演算順序によって結果が異なる組合せ爆発の危険性があるという留意はしておいたほうが良いです。もちろん、ケースバイケースで程度にもよりますが、必要な値はマイナスや逆数へ加工して取り扱うことにより、加法と乗法という安全なモノイドの演算に統一できるので、そのほうが予見できないバグの危険性は回避できます。 (3 + (-2) ) + (-1) = 3 + (-2 + (-1))(4 × 1/2) × 1/2 = 4 × (1/2 × 1/2) 15.5. モノイドの素晴らしさ③　単位元（Identity element）単位元とは、加法でいうと、ゼロ 00 + 5 = 5 =5 + 0 乗法でいうと、11 × 5 = 5 =5 × 1 文字列結合でいうと、"" "" + "Hello"= "Hello" = "Hello" +""配列結合でいうと、[]

[].concat([1, 2]) === [1, 2] // true[1, 2].concat([]) === [1, 2] // true

というように、二項演算のオペランドとして演算前と「等しい」結果を演算する特別な値です。 単位元（Identity element）

数学、とくに抽象代数学において、単位元（たんいげん, 英: identity element）あるいは中立元（ちゅうりつげん, 英: neutral element）は、二項演算を備えた集合の特別な元で、ほかのどの元もその二項演算による単位元との結合の影響を受けない。 (M, ∗) を集合 M とその上の二項演算 ∗ のなすマグマとする。S の元 e が存在して、S の任意の元 a に対してe ∗ a = a ∗ e = aを満たすときにいう。

なるほど、ではそういうものを満たす単位元の何がいいのか？ モノイドの素晴らしさ①　型（Type）が単一の閉じた二項演算モノイドの素晴らしさ②　組み合わせ方に依存しない、結合法則というのは、双方ともUSB工業規格であったりレゴブロックであったり、その「等しさ」のメリットが明白であり、複雑性を排除してくれるシンプルな二項という観点でたいへんわかりやすいのですが、モノイドの素晴らしさ③　単位元というのはちょっと毛色が違うというか、説明がしにくいです。 どの程度説明がしにくいのか？というと、加法におけるゼロ 0の存在の便利さを説明してみろ、というのと同じレベルで、あえていうならば、絶対に必要になってくることは日常レベルでも結構わかっているから、もし現代文明でゼロ０がなければ非常に世界が複雑になり困るだろう、という感じでしょうか。 実際に、単位元の有用性というのものはかなり認識しにくいので、認識もせず、使わなくてもそこそこイケる、というか、0　歴史

0 の起源ゼロの発明は、数学史の飛躍の一つである。紀元前2500年頃のピラミッドの幾何学的な正確性は、古代エジプト人が高度な数学を持っていたことを示す。しかし古代エジプトでは数学は主に暦法と土地測量の手法として発展したため、零の研究は発達せず、それを表す記号もなかった。面積がゼロの土地はなく、0日めのあるカレンダーもない。よってゼロは不要であった[。

という感じなで、実際に人類はゼロ０なしで高度な数学を使ったピラミッドでも建てられたらしいですから、単位元の有用さは当たり前のことだ、と説明するのはレゴブロックの結合性の有用性を説明するのとは多分レベルは違うと思います。 15.6. 半群（Semigroup）にはいつでも単位元を追加してモノイドにできるこのように、単位元なしで、結合性だけがある数学構造は、半群（Semigroup）といって、単位元のルールまで要請はせず、結合法則だけあればいい、というものです。

定義集合 S とその上の二項演算 •: S × S → S が与えられ、以下の条件結合法則S の各元 a, b, c に対して(a • b) • c = a • (b • c) を満たすならば、組 (S, •, e) を半群という。

少なくとも、人類がゼロ０を発明するまでは、世界の素朴な見方としては半群の世界でしょう。たとえば、小学校の算数の最初のほうでは、おはじきや数え棒みたいな算数セットを購入させられてそこから数という抽象概念を刷り込まれていくわけですが、 れい 0

1 から 1 を ひいた かず を れい と いいます。 レイは 0 と かきます。しき で かくと1 - 1 = 0です。「いち ひく いち は (わ) れい」と、よみます。0は、なにも、ない　かず です。だから、 かず に 0 を たしても、 かわりません。たとえば7 + 0 = 7「なな たす レイは (わ) なな」です。

と人類が結構最近発明したゼロという概念をしれっと当たり前のように教えてしまっています。 特に、

0 (レイ) の たしざん 0は、なにも、ない　かず です。だから、 かず に 0 を たしても、 かわりません。たとえば1+0=1　「いち たす レイは (わ) いち」0+1=1　「レイたす いち は (わ) いち」2+0=2　「に たす ゼロ (レイ) は (わ) に」0+2=2　3+0=3　4+0=4　10+0=10　「じゅう たす レイは (わ) じゅう」0+10=10　17+0=17　です。0+0＝0「レイたす レイ は (わ) ゼロ (レイ) 」です。レイをゼロ (レイ) ということはふつうありません。ただしここからはゼロ (レイ) と書きます。

というのは、小学生相手に結構な離れ業をやりのけています。そもそも、おはじきや数え棒、それからUSBデバイスやレゴブロックでも同じですが、人類の素朴な感覚としてはそういう具体的な物体は、結合法則が満たされていて便利だ、というのは直感的に理解していますが、それらが「ない」概念を扱うのは直感的ではないので、半群の概念しかないはずです。つまり自然数とは１から始まるものであり、自然数に０を含めるとする流儀は、歴史上は最近のことです。加法＋についても、その１からはじまる自然数として成立していた半群だったのですが、０をあとから発明して追加することにより、０と正の整数、負の整数と範囲が広がりました。 こういうトリックを単位元の添加といいます。 つまり、素朴な感覚としては結合性だけがある半群であっても、どうせすべての半群には、加法の単位元０のように、必ず単位元を追加できるので、小学校の授業のように、もう最初から半群ではなく単位元が込みのモノイドとして用意する、という理屈ですし、どうせモノイドとセットになっているようなFoldで単位元のことは必要になってきます。15.7. モノイドとFold（Reduce）の強力さ計算機科学におけるモノイド

計算機科学において、多くの抽象データ型はモノイド構造を持つ。よくあるパターンとして、モノイド構造を持つデータ型の元の列を考えよう。この列に対して 「重畳」(fold) あるいは「堆積」(accumulate) の操作を施すことで、列が含む元の総和のような値が取り出される。例えば、多くの反復アルゴリズムは各反復段階である種の「累計」を更新していく必要があるが、モノイド演算の重畳を使うとこの累計をすっきりと表記できる。別の例として、モノイド演算の結合性は、多コアや多CPUを効果的に利用するために、prefix sumあるいは同様のアルゴリズムによって、計算を並列化できることを保証する。

　1から10までの数を足すコードというのをみて、反射的にForループという制御フロー構文の列挙を考えるのが命令型プログラマであり、「モノイドのFold(畳み込み)のことか・・・」と考え、fold（reduce）という高階関数で、再帰的なデータ構造（モノイド）を分析し、結合操作（add）を使用して、その構成部分を再帰的に処理した結果を再結合し、戻り値を構築する依存グラフの式を書けば良い、とわかっていれば、関数型プログラマであると言えるでしょう。

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add); console.log(sum);

55 // sum

また、同時に、

別の例として、モノイド演算の結合性は、多コアや多CPUを効果的に利用するために、prefix sumあるいは同様のアルゴリズムによって、計算を並列化できることを保証する。

とありますが、モノイドというのは結合性（演算の順番に依存せず「等しい」）ことが保証されているので、なにかのクラウドの並列計算でも計算結果の正しさは保証されています。 命令型プログラミングというのは、コード自体が逐次処理であり、基本的にはフローのことしか考えていないので、並列計算というのは、まさに水と油の異なるパラダイムであり、これを解消したいとおもって、オブジェクト指向で誰かが発明したフレームワークを使えばいい、みたいなことが往々にして喧伝されているわけですが、根本的に、このようなモノイドという極めてシンプルで安全で堅牢な代数構造のこと、関数型プログラミングの基本的作法を知っていれば、そのような余計なフレームワークに手を出す合理性はまったくありません。 15.8. Fold（Reduce）と単位元Array.prototype.reduce()を含む各プログラミング言語のFoldの仕様には、一見不可解な仕様があり、

引数initialValue 省略可コールバックが初めて呼び出されたときの previousValue の初期値です。 initialValue が指定された場合は、 currentValue も配列の最初の値に初期化されます。 initialValue が指定されなかった場合、 previousValue は配列の最初の値で初期化され、 currentValue は配列の 2 番目の値で初期化されます。

実際、

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add); //1+2+3+4+5+6+7+8+9+10console.log(sum); // 55

では、initialValueは省略されています。この場合、initialValueを省略しない場合、その値は、加法＋の単位元の0となります。

const add = (a, b) => a + b;const sum = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].reduce(add, 0); //0+1+2+3+4+5+6+7+8+9+10console.log(sum); // 55

乗法では、

{ const multiply = (a, b) => a * b; const product = [1, 2, 3, 4].reduce(multiply); // 1 * 2 * 3 * 4 console.log(product); // 24}{ const multiply = (a, b) => a * b; const product = [1, 2, 3, 4].reduce(multiply, 1); // １ * 1 * 2 * 3 * 4 console.log(product); // 24}

と乗法の単位元である1が、initialValueとなります。多くの場合、単位元は省略できるのですが、あえて指定しなければならない局面はあります。 15.9. 論理演算もモノイドexprは式（expression）のとき、 論理和 (||)expr1 || expr2 論理積 (&&)expr1 && expr2 という論理演算もモノイドです。 a,b,c は true/falsex は true/falseのとき、 (a || b) || c = a || (b || c) false || x = x = x || falsefalse を単位元としたモノイド (a && b) && c = a && (b && c) false && x = x = x && falsetrue を単位元としたモノイド16. 関数（写像）の連鎖と関数（写像）の合成（Function composition）16.1. 関数（写像）の連鎖

という写像は、アロー関数式で、

というように関数 f が定義する表現ができますが、写像を連鎖させることができます。

346ABC+1+2+3346+1+2+3

const f = x => x + 1;const g = x => x + 2;

とすると、fx表記法では、

g(f(3)); // 6

となります。入れ子構造になっており写像のイメージで直感的ではないので、独自に実装した、パイプライン演算子（Pipeline Operator）を活用して、

P(3)['>'](f)['>'](g)　　// 6

と表現できます。16.2. 関数（写像）の合成（Function composition）このとき自然と、関数（写像）の合成という概念が出てきます。たとえば、fとgから合成された関数を fg とすると、

fg(3); // 6

P(3)['>'](fg) // 6

写像の合成（Function composition）

数学において写像あるいは函数の合成（ごうせい、英: composition）とは、ある写像を施した結果に再び別の写像を施すことである。 例えば、二つの写像 f: X → Y および g: Y → Z について、g の引数を x の代わりに f(x) とすることにより、f と g を「合成」(compose) することができる。直観的には、z が写像 g で対応する y の函数で、y が写像 f で対応付けられる x の函数ならば、z は x の函数であるということを述べている。 これにより、写像 f: X → Y と写像 g: Y → Z との合成写像 (composite function/mapping) が X の各元 x に対して とおくことによって定まる。"g ∘ f" は図式的に写像 f, g を施す順番とは逆順となるため、しばしば正順に "fg", "f ; g" などと記す流儀もみられる（後述）。

合成の記法について• g ∘ f の合成の記号を落として、単に gf と書かれることも多い。• 20世紀のなかごろ、（左から右へ読む文章中で）"g ∘ f" と書いたものが "最初に f を施してから g を施す" という意味になるのは非常にややこしいため、記号を改めて "f(x)" の代わりに "xf" と書き、"g(f(x))" の代わりに "(xf)g" と書いた者もあった。このような記法は後置記法と呼ばれる。分野によってはこのようにしたほうが、写像を左から作用させるよりも自然で単純であるようにも思われる（例えば線型代数学では x を行ベクトルとして、行列 f および g と右からの行列の積によって合成を行うことができる。行列の積は可換ではないから、順番は重要である）。連続して変換することと合成とが、合成の列を左から右に読むことによってちょうど一致する。• 後置記法を採用している文脈では、"fg" と書くことで、初めに f を適用してから g を適用するという意味となるが、後置記法では記号の現れる順番を保たなければならないので、"fg" と書くのは（どこまでが一つの記号なのかわかりにくいため）曖昧さを含んでしまう。計算機科学者はこれを "f;g" と書き、これによって合成の順番に関する曖昧さを除くことができる。

本稿では、合成関数について、g ∘ fという記法ではなくf.g あるいはfgと表記します。また引用で言及されているセミコロン（；）を関数合成演算子のシンボルとする、というのは、そんなポピュラーではないと感じますし、特にJavaScriptでセミコロン（；）というのは、まったく違う意味なので引用箇所はともかく、本文では避けます。16.3. 関数（写像）合成（Function composition）は二項演算f と g という2つの関数（写像）の合成というのは、f と g という2つの関数の間の二項演算 f . g であると捉えることができます。ここで、.　は二項演算子です。 パイプライン演算子（Pipeline Operator）を活用して、3 > f > g

P(3)['>'](f)['>'](g)　　// 6

と表現して、さらに、a > f >g = a > (f . g)fg = f.g3 > fg3 > (f.g)

const fg = f['.'](g);P(3)['>'](fg); // 6P(3)['>']( f['.'](g) ); // 6

となるような関数合成の二項演算子を定義することができます。 基本的には、オブジェクト指向のメソッドを関数型の二項演算子として置き換えるJavaScriptで独自の二項演算子（Custom operator）を定義するで説明した手法を踏襲しますが、特にTypeScriptのコードは簡単ではありませんし、ここで一気に実装までやってしまうと、肝心の関数（写像）の合成それ自体の概念説明にとってオーバーヘッドが大きくなりすぎて論点がブレてしまうので、かなり後回しにします。今のところは、実装できた、という前提で話をすすめます。 16.4. 関数（写像）合成（Function composition）はモノイド（Monoid） 写像の合成（Function composition）

写像の合成は、それが定義される限りにおいて常に結合的である。すなわち、f, g, h がそれぞれ（合成が定義できるように）適当に選ばれた始域および終域を備えた写像であるとするならば、 が成り立つ。 ここで、括弧はそれが付いているところから先に合成を計算することを指し示すためのものである。これは括弧をつける位置の選び方は写像の合成の結果に影響を及ぼさないということを意味しているから、括弧を取り除いても意味を損なうことは無く、しばしば括弧を省略して f ⋅ g ⋅ h と書かれる。写像の数がさらに増えても同様である。

写像の合成は、二項演算であり、それが定義される限りにおいて常に結合的ということは、要するに写像の連鎖が成立している限り、結合性がある半群（Semigroup）であり、半群には必ず単位元がいつでも追加できるのは保証されているので、写像の合成はモノイドです。 これから、そのことについて説明、証明していきます。 関数（写像）の連鎖の例にふたたび注目します。

346ABC+1+2+3346+1+2+3　　ここで、関数（写像）はf: +1g: +2と２つあって、写像が連鎖した結果、f.g: +3という関数合成ができているということでした。 どうしても、必要、というわけでもないですが、全く同じグラフを

346+1+2+3 このように、トライアングルにすることができます。 まずデメリットは、いきなりこのグラフを示されると、最初の数直線的なグラフのイメージが湧きにくいことがあります。メリットは、まず f.g: +3 の合成関数が曲線で書かなくてすむことや、また、そもそも関数というのは、+1,+2というような数直線上に並ぶ四則演算とは限らないので、より抽象的な操作ぽいこと、それから後々わかりますが、このほうがスペースを効率的に使っており、あとからグラフを追加しやすい、ことなどがあるでしょうか。 そのとおり、より抽象的に表現すると、

ABCfgf⋅gf:A→Bg:B→Cf⋅g:A→C a> f⋅g =a>f> g =c これが、関数 f と g と合成された関数である f.g の一般的なイメージとして使えます。 16.5. 関数の合成という二項演算には結合性がある 関数合成自体が二項演算であることはすでに説明しましたが、 では関数合成という二項演算を連鎖するとどうなるでしょうか？？別に複雑なことはなく、単にこういうことです。

+3+2+16439+3+5 f: +1g: +2それから合成関数であるf.g: +3にさらにつけ加えて、h: +3です。 これをトライアングルのグラフに描き直すことができます。

+5+3+3+2+19643 Dとhを付けて h:C→Dg⋅h:B→D

g⋅hf⋅ghgfDCBA(f⋅g)⋅h=f⋅(g⋅h) 関数合成という二項演算は、連鎖が成立している限り必ず結合性があるのがわかります。 命令型プログラミングのマインドセットになっていると、こういう「自由自在」の関数合成の二項演算の結合性（つなげる順序で結果が変化せず「等しい」）という話になった場合、「そんな都合よく？」と思いがちです。理由は、暗黙に時間依存する関数を取り扱うことが当たり前なので、関数を組み合わせる順序によって結果が変化して、コードが当初の想定から外れて壊れてしまうからです。 純粋に関数に渡される引数とその他定数だけか、もしくは時間依存していても明示的に時間依存グラフを構成しているFRPの値のみで構成されている、いわゆる「純粋」な関数の合成ならば、組み合わせる順序に依存せず等しくなる結合性が必ずあります。 16.6. 関数の合成という二項演算には左右の単位元が存在する 恒等関数(identity function)id: x→xは関数合成という二項演算の単位元です。 f:A→B （これにはもちろんid自身も f にふくまれる）id:A→A id:B→B が自明なこととして上の図を再構成すると

f⋅idid⋅fidfidBBAA id⋅f=f=f⋅id 関数合成演算は結合性があり、結果的にleft-right identity左右の単位元idがが自動的に存在している。 16.7. 関数合成という二項演算はモノイド（証明終わり） (1)(f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)(2)id ⋅ f=f=f ⋅ id と結合性があり、左右の単位元が存在しているので、関数合成はモノイドです。 極めて重要なことなので念の為に繰り返しますが、関数合成という関数型プログラミングで極めて根本的な二項演算において、結合性があること、

括弧をつける位置の選び方は写像の合成の結果に影響を及ぼさないということを意味しているから、括弧を取り除いても意味を損なうことは無く、しばしば括弧を省略して f ⋅ g ⋅ h と書かれる。写像の数がさらに増えても同様である。

(f⋅g)⋅h=f⋅(g⋅h) が成立しているということは、グルーピング演算子（）の位置は気にする必要がなく（）をつけてもつけなくても「等しい」ことf ⋅ g ⋅ h が保証されているわけですから、組み合わせ爆発の危険性がない、安全な代数構造である、ということを意味しています。 17. 高階関数（Higher-order function）17.1. 関数の合成（Function compositon）と高階関数（Higher-order function）という用語ようやく高階関数（Higher-oder function）の説明にまで辿り着きました。これまで何度か高階関数という言葉を出さざるを得ないほど、関数型コードにとっては必要な概念です。 高階関数とは関数の組み合わせ方法のひとつで、前述の関数合成とあわせて、 • 関数の合成（Function compositon）• 高階関数（Higher-oder function） というのが、おおまかな関数の組み合わせの方法のツートップであると言えるでしょう。 ところが、日常的な言語感覚でいうと、今から説明するほうの高階関数（Higher-oder function）のほうが、関数の合成（Function compositon）の意味に近いです。 そして、関数の合成（Function compositon）というのは、前述のとおり二項演算であり、まさに二項演算の定義そのものとして「連結（Concat）」という用語のほうがその素性を正確に表現しています。 用語の命名というのは非常に重要で、もし • 関数の合成（Function compositon）→　関数の連結 / 連結関数（Function concatenation/ Joint function）• 高階関数（Higher-oder function）→　関数の合成 / 合成関数（Function compositon / Composed function） とすれば、より数学や関数型プログラミングの理解が簡単になった、と思います。こういう用語の混乱というのは、数学そのものでもそうですし、プログラミング分野ではあまり注意を払われておらず、あとから概念を学習する学習者の負担になっていますが、解説書でもろくに注意を払われず、大上段から「高階関数という」とだけ説明されていることがほぼすべてですし、じゃあむしろ高階関数の概念そのものに近い語感である関数の合成（Function compositon）との関係はどうなっているのか？ということもほぼ説明はされていません。 本稿ではそこも含めてきちんと解説していきます。 17.2. 高階関数（Higher-order function）は世界にありふれている まず、前述のとおり、• 高階関数（Higher-oder function）→　関数の合成 / 合成関数（Function compositon / Composed function）という言葉の意味に近いということを念頭においてください。 前述の従来表現の関数の合成 / 合成関数（Function compositon / Composed function）が、二項演算であり２つの関数の連結で、その二項演算を連鎖して、モノイドだ、とやったわけですが、連結、連鎖という「左から右」の方向に組み合わせであるといえます。 他方でこちらの高階関数（Higher-oder function）というのは、その名の「高階（Higher-oder）」のとおり、「上下方向」で積み増して合成する組み合わせであると言えます。 もちろん、念の為ですが抽象概念であるので、本当は左だの右だのはないわけですが、実際に数式は左右に並んでおり、連結方向で、左と右とは表現しますし、その左右方向の接続とは異なる、というのであれば、上下方向である、と表現してもそんなにデタラメであるというわけではないはずです。 高階関数（Higher-oder function）というのは、実は世界にありふれていて、その概念の理解は難しくありません。 たとえば、コンピュータのハードウェアというのは、ひとつのよくできた関数です。さらに、その各種ハードウェアの仕様に沿ったOS(オペレーティング・システム)という基本ソフトウェアというのも、関数です。 ハードウェアにOSをインストールすることで、これら2つの関数を合成可能です。 • ハードウェア（Windows）= Windowsマシン• ハードウェア（MacOS）= Mac• ハードウェア（Linux）= Linuxマシン これが高階関数（Higher-oder function）です。もちろん、すべてのハードウェアに任意のOSがインストールできるわけではなく、最初から高階関数としてうまく仕様を一致させておく必要があります。• Androidスマホハードウェア（Android）• iPhone（iOS）と互換性がまったくないハードウェアは当たり前に存在しています。 こういう高階関数は、そもそものあり方として入れ子構造になっており、 • Windowsマシン(Chromeブラウザ) • Mac(Chromeブラウザ) • Linuxマシン(Chromeブラウザ) と、今度は、各種OSという基本ソフトウェアの上にアプリケーション・ソフトウェアをインストールすることで、より高度な目的の関数合成ができます。 OSというのはシステムソフトウェアであり、アプリケーションソフトウェア（application software、最近は略すとapp(s)）と対になる概念です。

アプリケーションソフトウェア（英: application software、最近は略すとapp(s)）は、ある特定の機能や目的のために開発・使用されるソフトウェア[1][2] で、コンピュータの操作自体のためのものではないもの[2]。たとえば、ワープロソフト、表計算ソフトウェア、イラスト作成（お絵かき）用ソフトウェア、写真加工用ソフトウェアなど。 アプリケーションと（2番目の語を省略して）も呼ばれ[1]、特に最近ではアプリと略されることも多い[1]。「アプリケーション」は「応用」という意味なので日本語では「応用ソフト」とも呼ぶ[1]（が、最近はかなり使用頻度が減った）。アプリケーションプログラム（応用プログラム）ともいい、コンピュータ・プログラムの一種である。

このように、「OSにアプリをインストールする」ということは、特にスマートフォンの普及以降ではIT技術者のみならず、一般人が日常的に繰り返している、高階関数（Higher-oder function）、関数合成の行為であると言えます。 さらに、Chromeブラウザや、AdobeのPhotoshopなどでもエクステンションやプラグインと呼ばれる追加機能があり、これも高階関数（Higher-oder function）です。 • Chromeブラウザ（エクステンション）• アプリ（プラグイン） つまり、

プラグイン関数

アプリ関数

OS関数

ハードウェア関数

こういうレイヤを下から上の方向へ積み増すことは、高階関数（Higher-oder function）を作り出しているということになります。 あるいは、もっと範囲を広げると、すべての「設定（Setting）」というのは高階関数であると言えます。 Google検索が関数であることは説明しました。

Googleの検索エンジンは巨大なデータベースで、膨大なWeb記事がランキングされてストックされています。Google検索も、検索ワードがインプット、検索結果がアウトプットの関数です。 検索ワードをインプットしたら検索結果をアウトプットする Google関数 検索ワード検索結果Google関数=検索エンジン Google関数を使う 緑茶Google関数=検索エンジン日経平均株価Google関数=検索エンジン

このとき、Google検索は、暗黙に裏側で設定、あるいはパーソナライゼーションというものがなされていて、

この設定は、各種のインプットがあり設定が保存されて反映されるアウトプットがある関数になっています。つまり、Google検索（設定） = パーソナライズされたGoogle検索という高階関数になっています。 17.3. パイプライン演算子をつかって高階関数を表現する

プラグイン関数

アプリ関数

OS関数

ハードウェア関数

こういうレイヤを下から上の方向へ積み増す高階関数（Higher-oder function）をパイプライン演算子（Pipe Operator）をつかって表現してみましょう。 アプリ関数（プラグイン関数）• というのは、データファーストのパイプライン化すると、プラグイン関数 > アプリ関数 と表現できます。 ユーザ入力 > (プラグイン関数 > (アプリ関数 > (OS関数 > ハードウェア関数))) という構造になっていることがわかります。もっと抽象的に、ユーザ入力 a関数 f, g で表現するらば、a >(f>g) 17.4. 関数の合成（Function compositon）と高階関数（Higher-order function）の比較ここで、従来表現の関数の合成（Function composition）は関数の連結であり、二項演算であり関数合成の二項演算子をつかって表現することもできるモノイドでした。まとめると、 関数の合成（Function composition）a > f > g = a > (f . g) fg = f . g 高階関数（Higher-oder function）a >(f>g) fg = f>g 17.5. 関数同士の組み合わせでない高階関数用語と定義と分類の問題ですが、以上のように関数２つを上下に積み上げてより高度な関数を合成する、という以外に、インプットあるいはアウトプットのどちらかひとつでも関数であれば、それも高階関数と呼ぶ、という決まりになっているようです。高階関数

高階関数（こうかいかんすう、英: higher-order function）とは、第一級関数をサポートしているプログラミング言語において少なくとも以下のうち1つを満たす関数である。 • 関数（手続き）を引数に取る• 関数を返す

17.6. 高階関数（Higher-order function）とラムダ式（アロー関数式）高階関数のざっくりとした一番外側の概念を理解したところで、次は具体的な実装を具体的な表記とともに研究します。 表記というのは非常に重要です。逆に言うと表記を軽んじていると、単純なケースに限ってはうまくいくだろうというある種のプログラミングの複雑性にまつわるリスクへの楽観視、軽視や思い上がりで、結局複雑性によってバグまみれのコードを書くことになります。 すでに説明したとおり、高階関数というものは非常にありふれた当たり前の概念なのですが、ES6のラムダ式（アロー関数式）の導入以前は、function文、あるいは中途半端なfunction式しか存在しなかったため、普通のこと、つまり高階関数の取り扱いをするのにも地獄のような様相でした。JavaScriptはES6のラムダ式導入以前と以降でまるで別モノで、ES6以降は、関数型プログラミング、つまり式の表現が飛躍的に楽になりました。

アロー記法の関数の定義 アロー関数式です。もちろん文ではなく式であり、プログラミング界隈ではラムダ式という名称のほうが有名で通用しやすいはずです。 簡潔で美しいですね。無駄を取り去った機能美です。 xとyはプレースホルダであることを考慮して、x が x + 1 に写像される、というイメージそのままになっています。 ラムダ式（アロー関数式）は写像を表現するプレースホルダだけで構成されています。 そして、この x というのはあくまでプレースホルダにすぎないので、 別のシンボルたとえば a であっても全く同じ意味になります。 そして、その上でここには、プレースホルダではない、意味がちゃんとある名前である関数名の f はありません。関数に名前をつける、という行為はまた別の概念だからですね。別の概念ならば一緒くたにせずに、表記としてもしっかり分離したほうが、このようにプレースホルダのシンボルなんだから別のシンボルでも構わない、であるとか、関数名はプレースホルダではないので命名には特段の意味がある、という概念の混同が発生していません。それに関連もしますが、概念の粒度が小さいので混乱もないし構成の自由度で優れています。こちらの表記のほうが概念的にミニマルでコンパクトで、写像（Map）の概念そのままのイメージ的に自然なのですが、あまりにも、f(x) という関数名とプレースホルダは同時にセットで定義する、混沌とした数学の流儀が当たり前に数学世界とプログラミング世界に浸透しているため、ラムダ式は無名関数という奇妙なネーミングさえあります。 もし関数名が必要なのであれば、単純に、 というように関数名 f を別途割り当てて定義すれば良いだけです。

17.7. ラムダ式（アロー関数式）で遊ぶ identity関数もっともシンプルなラムダ式は恒等関数(identity function)です。

関数の合成という二項演算には左右の単位元が存在する 恒等関数(identity function)id: x→xは関数合成という二項演算の単位元です。 f:A→B （これにはもちろんid自身も f にふくまれる）id:A→A id:B→B が自明なこととして上の図を再構成すると f⋅idid⋅fidfidBBAA id⋅f=f=f⋅id 関数合成演算は結合性があり、結果的にleft-right identity左右の単位元idがが自動的に存在している。

const identity = a => a;

ちなみにTypeScriptではインプットは任意のタイプなのでジェネリックでこのように表現できます。

const identity = <A>(a: A) => a;

インプットはそのまま素通りしてアウトプットになります。

identity(5) // 5

17.8. ラムダ式（アロー関数式）で遊ぶ right関数ここで、恒等関数であるidentityをアウトプットにもつ高階関数を定義します。

const right = a => identity;

どうなるでしょうか？

right(5) // [Function: identity] a => a

当然の如く、identity関数が返ってきました。インプットである５は無視されています。right(5) = identity 関数であるので、この関数にさらに値が入るはずです。

right(5)(3) // 3

identity関数に3を適用したので、3が返ってきました。 Chromeブラウザ > F12 > Console

さてここで、

const right = a => identity;

rightの定義のidentityは、

const identity = a => a;

と定義されているので、そっくり置き換えて

const right = a => a => a;

と書きなおせます。

right(5)(3) // 3

この場合でも、全く同じ挙動です。書き換える前の関数と同じものだからです。より意味的にわかりやすく

const right = a => 　　　　　　　　　　a => a; //identity

このような構造となっており、最初のほう、上段のaのインプットは捨てられます。下の段がidentity関数であり、この下段のaのインプットが素通りして出てきます。この構造をわかりやすくするために、

const right = a => (identity);

と予めグルーピング演算子（）で分けておいて、

const right = a => (a => a);

としても構いません。同じものになります。今後は、ためしに、

const right = (a => a) => a;

としてみます。このとき、

const right = (identity) => a;

と同じものになるはずですが、この構造ではアウトプットのaに該当するインプットが存在しないことになってしまっています。実際に、

とエラーになってしまいました。意味不明に無闇矢鱈にアローシンボルを()で括ると、構造が壊れかねないということがわかります。ラムダ式は所詮プレースホルダだけで構成されているので、

const identity = a => a;

ではなくて、

const identity = b => b;

と考えて、

const right = a => identity;

は、

const right = a => (b => b);

あるいはカッコは不要なので、

const right = a => b => b;

としておれば、間違いないです。こうしておけば、

const right = (a => b) => b;

としてしまうと明らかに定義上おかしいプレースホルダの配置になっていることがわかります。逆に言うと、このような高階関数で、意味がわかっておれば、（）はつけても構わないし、後々自身や別のレビュワーが高階関数の意味を解釈しやすいようにあえて（）をつけておくことも賢明な方法です。また、

const right = a => b => b;

を使うとき、

right(5)(3) // 3

となりますが、これはidentityを一旦忘れて見方を変えると、rightという関数に5と3という２つの値が左右に入って、そのうち、左側の5は無視されて捨てられてしまい、右側の3だけが素通りしてでてくる、という関数であると考えることもできます。 17.9. ラムダ式（アロー関数式）で遊ぶ log関数こんなことをして何か役に立つのか？というと、役立ちます。 こういうlog関数をright関数を利用して定義します。

const log = a => 　　　　　　　right(console.log(a))(a);

log関数はインプットとしてaを取るのですが、right関数はインプットとして、• console.log(a)• aという2つの値を取ります。 JavaScriptは、先行評価（Eager evaluation）

先行評価（せんこうひょうか、英: eager evaluation）、正格評価（せいかくひょうか、英: strict evaluation）、厳密評価とは、プログラミング言語における評価戦略の一種であり、多くの言語処理系で標準的に使われている戦略である。概要先行評価では、変数の値が得られた時点で即座に数式が評価される。一般に、評価の済んでいない数式を表す中間的なデータ構造を構築・管理する必要がないため、単純なプログラミング言語ではこれが最も効率的である。

なので、()の中の引数はEager（熱心）に、与えられた途端に評価してしまいます。その結果、console.log(a)が即座に実行され、undefinedという値が返ってくるのですが、これはright関数なので、その左の値は無視されて捨てられてしまいます。結果、右側のaだけがすり抜けて出てきます。大枠では、最初に与えられたほうの左側の値は捨てられ、あとの右側の値はidentity関数を通ってそのままアウトプットになりますから、log関数というのはinput aoutput aとなっていて大枠ではidentity関数と同じような挙動を示します。違うのは、その値aをコンソールに表示してくる、ということです。 このlog関数は、元のコードにとってはidentity関数と同じインパクトしかない、つまりスリぬけるだけなので、コードの挙動を確認するDebugに使えます。命令型コードのように、値がコロコロと変化するわけではないのですが、それでも関数型コードの構造が正しいことを確認するために、この値はどうなっているんだ？と確認したいときに、しれっとこのlog()で、その値を囲むだけで、Debug対象のコードに全くインパクトを与えることなしで、コンソールに値を表示して確認することができるわけです。また、console.log()と打つのは長いので、代わりにlog()関数を使うこともできます。 17.10. right関数で命令型コードの順次実行をエミュレートしてしまうこのように、right関数は、log関数の実装のために使えますが、要するに、関数型コードのグラフ構造、依存グラフと関係ないところで、IO(入出力)をしたい、とにかくある値をコンソールの出力しておいて、そのconsole.log関数の返り値などどうでも良いので捨てた上で演算を継続したいときに役立ちます。 あるいは、IOを広く捉えると、right関数の左側では、メモリへの値の書き出し、これはつまり関数型コードではアンチパターンの値の更新であるわけですが、その値の更新を済ませたあとで、right関数の右側で、その左側でやってのけた更新された値に依存する演算をする、という利用方法があります。 そして実は、両者ともに、命令型では普通にやっている、文（Statement）の上下の羅列による順次実行と全く同じことです。たとえば、right関数を利用したlog関数

const log = a => 　　　　　　　right　　　　　　　　(console.log(a))　　　　　　　　(a);

は、

const log = a => { console.log(a); return a;};

という命令型のコードを書いているのと全く同じです。 関数型コードでも、たとえば、特に、本書であとからやるFRPの実装では、原理的にIOを弄り倒すので、そういうIOと関与しない範囲の関数型コードではアンチパターンである、このような命令型の列挙をしたくなる局面が非常に多いのです。そこで諦めて｛｝を使って、冗長なreturn文（Statement）などを書きたくない場合は、right関数を利用することで、あくまで式（Expression）としてスッキリと書き下すことが可能になります。 このように、ただ値が素通りするだけのidentity関数って一体なんの意味があるのか？なんの役に立つのか？とか、identity関数から構成したrightという高階関数はなんの意味があるのか？という至極当然の疑問が当初あっても、使い方によって下手なDebugツールを使うよりも便利なlog関数を構成できたり、また命令型コードの順次実行をエミュレートできたりと、高階関数はこれだけシンプルなレベルでも非常に大きな力を秘めています。 17.11. コンビネータ論理実際この高階関数のバリエーションは、 コンビネータ論理

コンビネータ論理（英: combinatory logic、組み合わせ論理）は、モイセイ・シェインフィンケリ（ロシア語版、英語版）（露: Моисей Эльевич Шейнфинкель、英: Moses Ilyich Schönfinkel）とハスケル・カリー（英: Haskell Brooks Curry）によって、記号論理での変数を消去するために導入された記法である。最近では、計算機科学において計算の理論的モデルで利用されてきている。また、関数型プログラミング言語の理論（意味論など）や実装にも応用がある。コンビネータ論理は、コンビネータまたは引数のみからなる関数適用によって結果が定義されている高階関数、コンビネータに基づいている。

SKIコンビネータ計算

SKIコンビネータ計算は型無しラムダ計算を単純化した、ひとつの計算モデルである。このモデルは、ある種のプログラミング言語と考えることができるが、人間によるソースコードの記述には適さない（難解プログラミング言語には時折採用される）。その代わり、このモデルは非常に単純なチューリング完全な言語であるため、アルゴリズムの数学理論においては重要である。また関数型言語を実行する抽象機械のモデルとして使っている例もある[1]。 ラムダ計算におけるあらゆる演算は、SKIにおいて3つの定数記号S, KおよびI（これらをコンビネータと呼ぶ）および変数記号によって表現できる。2引数の関数適用演算のみを持つ形式言語の構文木と考えれば、定数記号と変数記号を葉とする二分木と捉えることもできる。 実際には、 I はモデルを簡単にするために導入されたものであり、SKIシステムを展開するにはSとKの2つで十分である。

B,C,K,Wシステム

B, C, K, Wシステムは、基本的な4つの定数記号 B, C, K, W からなるコンビネータ論理の変種である。この体系はハスケル・カリーの博士論文Grundlagen der kombinatorischen Logikによるもので、その結論部分はCurry 1930において示された。

など研究しつくされています。ラムダ計算、関数型プログラミングの理論的基礎となっていますが、コーディングの実用上はどの程度深入りするか？は好奇心の問題と言えるでしょう。 しかし、identity関数ってなんの役に立つのか？right関数は？と純粋に理論的であると思っていたものに思わぬ実用性が見いだせたりすることが往々にしてあります。 17.12. 2+引数関数は使わず単項関数（Unary function）を使う　関数の合成や高階関数を使いこなせるようになって、そのパワフルさ、便利さを体感しはじめると、その力の源泉は、単項関数（Unary function）であることがわかってきます。理由はかんたんで、2引数以上の関数であれば、連結するとき（関数の合成）や高階関数として合成することが極めて厄介になるからです。単項関数は、ある意味、規格が1引数と決め打ちされており、それ以上でもそれ以下でもない、と厳密に規定されている、扱いやすいのです。実際に前述のコンビネータ論理では単項関数のみの体系にすることが可能です。 またそこまで踏み込まずとも、たとえば、 関数の合成（連結）の結合性を考えるとき、

h:C→Dg⋅h:B→D g⋅hf⋅ghgfDCBA(f⋅g)⋅h=f⋅(g⋅h) 関数合成という二項演算は、連鎖が成立している限り必ず結合性があるのがわかります。

それから、高階関数を合成しようとしているとき、

パイプライン演算子をつかって高階関数を表現する プラグイン関数 アプリ関数 OS関数 ハードウェア関数 こういうレイヤを下から上の方向へ積み増す高階関数（Higher-oder function）をパイプライン演算子（Pipe Operator）をつかって表現してみましょう。 アプリ関数（プラグイン関数）• というのは、データファーストのパイプライン化すると、プラグイン関数 > アプリ関数 と表現できます。 ユーザ入力 > (プラグイン関数 > (アプリ関数 > (OS関数 > ハードウェア関数))) という構造になっていることがわかります。もっと抽象的に、ユーザ入力 a関数 f, g で表現するらば、a >(f>g)

もしfやgの接続、つまり引数の数、インプットの数が1つに統一されていないのであれば、非常に厄介なことになる、というのは直感的に理解できるのではないでしょうか？ 17.13. カリー化(currying)99の表を考えます。 以下の表では、たまたま0まで含まれていますが本質ではないです。

値を求めるための関数を素朴に考えるならば、それはインプットとなる引数が２つの二項関数（Binary function）で、

const table = (a, b) => a * b; table(3, 5) //15

となるでしょう。 しかし、このような2引数関数、二項関数（Binary function）は使わず単項関数（Unary function）を使いたいので、高階関数を使って、

const table = a => b => a * b; table(3)(5) //15

と書くこともできます。 自分で最初から実装するときは自由に単項の高階関数でやればいいのですが、概念的に最初二項以上の関数を単項関数に修正することを、カリー化（currying）といいます。

カリー化 (currying, カリー化された=curried) とは、複数の引数をとる関数を、引数が「もとの関数の最初の引数」で戻り値が「もとの関数の残りの引数を取り結果を返す関数」であるような関数にすること（あるいはその関数のこと）である。クリストファー・ストレイチーにより論理学者ハスケル・カリーにちなんで名付けられたが、実際に考案したのはMoses Schönfinkelとゴットロープ・フレーゲである。 関数 f が の形のとき、f をカリー化したものを g とすると、 の形を取る。uncurryingは、これの逆の変換である。理論計算機科学の分野では、カリー化を利用すると、複数の引数をとる関数を、一つの引数のみを取る複数の関数のラムダ計算などの単純な理論的モデルと見なして研究できるようになる。

今回、この99の表の関数を素朴に二項関数（Binary function）で実装し、

const table = (a, b) => a * b; table(3) //　NaN

このように、二項関数であるのにも関わらず、1引数だけを満たして関数適用した場合、

NaNが返ってきて、これ以上使い物にはなりません。 他方で、二項関数ではないカリー化された単項関数で実装したときは、

const table = a => b => a * b; table(3) // b => a * b

今度は、b => a * bという関数が返ってきました。 最初の引数であるaは3として適用済みで、残った引数であるbを適用したら、最終的な値を出しますよ、ということです。

const table = a => b => a * b; table(3) // b => a * btable(3)(5) //15

これは素朴に二項関数で実装するよりも柔軟でたいへん素晴らしいことです。

const table = a => b => a * b; table(3) // b => a * b

となっているとき、実際これは、全体の99の表から a=3 という値で絞り込んだ、

という「3の段」の表を表す関数を返していると見做せます。そしてこの「3の段」関数に、さらにb=5となる値を与えれば15という計算結果が返ってきます。 17.14. カリー化(currying)する関数とアン・カリー化（uncurrying）する関数二項以上の関数を単項関数に加工するための、カリー化(currying)する関数その逆の、アン・カリー化（uncurrying）する関数は、引数の数を限っておれば結構かんたんに実装できます。 Before:カリー化されていない関数（uncurried funciton） After: カリー化された関数（curried function） という関数（currying）

const curry = f => //before (uncurried) a => b => f(a, b); //after (curried)

Before:カリー化された関数（curried function） After: カリー化されていない関数（uncurried funciton） という関数（uncurrying）

const uncurry = f => //before (curried) (a, b) => f(a)(b); //after (uncurried)

これらの関数の実装でも高階関数を自由に活用しています。 これらはパラメータが2個の関数を扱うもっともシンプルなケースですが、3個の場合でもabcと増えるだけで同じようになります。パラメータの個数が決まっていない、というよりどんなパラメータ数の関数でも扱えるようにするには、もうちょっと工夫が必要で複雑になってきますが、ここでは踏み込みません。 ちなみにこの章では、高階関数の概念の説明に注力するために、あえて型（Type）は外しています。より厳密で実用的な関数型コードではもちろん高階関数であっても型（Type）は積極的につけていきます。 18. 独自の二項演算（Custom operator）、関数合成の二項演算子、パイプライン演算子の実装18.1. 道具立てを揃える 　関数の組み合わせ方法　 • 関数の合成（Function compositon）• 高階関数（Higher-oder function） あるいは、 • 関数の合成（Function compositon）→　関数の連結 / 連結関数（Function concatenation/ Joint function）• 高階関数（Higher-oder function）→　関数の合成 / 合成関数（Function compositon / Composed function） というところまで終わったので、これで関数型プログラミングの初歩レベル、と言っても世間一般でいう初歩ではなく、相当詳細にしっかり網羅できたと思います。このことは次のレベルに進むにあたりたいへん重要です。 この章では、これまでの知見を踏まえて、忘れないうちに早めに道具立てを揃えておきます。 その上で、続く章からより深く実用性も兼ね備えた理論面に続きます。 次の項目は、あえて、すでに書かれた項目のまるまるコピペです。その次の項目が、そのコピペの流れの続き再開ということになります。18.2. JavaScriptで独自の二項演算子（Custom operator）を定義するJavaScriptでは現在このような機能はありません。tc39/proposal-operator-overloadingという既存の演算子のオーバーロードの検討はあるにはありますが、まったく活発ではないようですし、残念ながらTC39にはあまり期待できません。 しかし、多少のハック的手法を許容するならば、なんとかはなります。それが本書の手法です。すべては二項演算子を活用するという根幹の目的を達成するためです。逆にこの最難関ポイントを突破することさえできれば、関数型プログラミングの見通しがクリアになり、視野は広がり、理解を深めることが容易になります。 では、はじめてみましょう。 シンプルなお馴染みの + という二項演算子を用いた、加法の二項演算 1 + 2 = 31 + 2 + 3 = 6 は、＋という二項演算子によって、JavaScriptのオブジェクトとしてNumberとNumberいう集合同士からNumberが演算される、と代数的に定義されています。 これは、オブジェクト指向の世界に翻訳すると、Numberオブジェクトに＋(Number)というメソッドが実装されていてNumberを返すということと同じです。つまり、

Object.defineProperty( Number.prototype, "plus", { value: function (R) { // R is Right hand side or the Binary operator return this + R; // `this` is Left hand side of the Binary operator }});

と、Numberオブジェクトにplusメソッドを拡張してやることで、

(1).plus(2); // 3(1).plus(2).plus(3); // 6

とオブジェクト指向の表記で記述することも可能です。 さらに、plusではなく本当に + という記号で拡張定義することも可能です。

Object.defineProperty( Number.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this + R; // `this` is Left hand side of the Binary operator }});

この場合は、オブジェクト指向的な . (ドット)記法ではSyntaxErrorになるので、代わりにプロパティ/連想配列形式でうまく書けます。

(1)['+'](2); // 3(1)['+'](2)['+'](3); // 6

と車輪の再発明をすることも可能です。 同様に、Arrayオブジェクト に+ という記号のプロパティでArray.concat() というメソッドを拡張してしまいます。

Object.defineProperty( Array.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this.concat(R); // `this` is Left hand side of the Binary operator }});

このコードでは、this.concat(R) と単純にArrayオブジェクトメソッドを + というオブジェクトプロパティにコピーしています。その結果、

array1.concat(array2);array1['+'](array2);

となります。

["a", "b", "c"] + ["d", "e", "f"]; // ["a", "b", "c", "d", "e", "f"]

と書くのは言語仕様的に無理でも、

["a", "b", "c"]['+'](["d", "e", "f"]); // ["a", "b", "c", "d", "e", "f"]

と書くことは可能になりました。 JavaScriptで独自の二項演算子（Custom operator）を定義することに成功しました。 Object.defineProperty()では、デフォルトの設定では、プロパティの値は変更することはできず、プロパティ列挙可能性がfalseになります。プロパティの列挙可能性と所有権

列挙可能プロパティは、内部の列挙可能enumerableフラグが true に設定されているプロパティです。これは、単純な代入や初期化で作成されたプロパティのデフォルトです (Object.defineProperty で追加したプロパティはデフォルトで列挙可能性が false になります）。

18.3. JavaScriptで独自の二項演算子（Custom operator）を定義するための関数前項を一般化します。この作業をここまで保留していたのは、高階関数を全力で活用するからです。高階関数の知識がないと、一体何をやっているのかわけがわからないでしょうし、誤魔化しながら説明するのは無理があったからです。 まず、plus関数を定義してみましょう。素朴な感覚では、左右にオペランドがある二項演算なので、引数が2つの二項関数の定義になります。つまり、すでに説明した以下のとおりの考え方です。

では実際に、式を組み立てていくとして、もっとも単純なコードは何でしょうか？ おそらくもっとも単純な式とは、 1 あるいは "hello" こんな感じでしょう。これがもっとも単純な関数型のコードです。 ではもう少し進んで、 1 + 2 より関数型コードらしくなりました。なぜならば、関数（Function）と演算子（Operator）は本当は同じもの二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y) であることはすでに確認済みなので、1 + 2 は実際に関数（Function）を扱う式（Expression）である関数型コードです。よく考えると、我々は全員、小学校の義務教育の範囲内ですでに関数型コードを書いていた、ということになります。

plus(1, 2) = 3

const plus = (L, R) => L + R;

ラムダ式のプレースホルダの名前は、a, b などでは、あとあと混乱するので、二項演算の• 左オペランド: L• 右オペランド: Rとして表現しています。表記の工夫は非常に重要です。

関数（Function）と演算子（Operator）は本当は同じもの二項演算（Binary operattion）x ◦ y とは二項関数（Binary function）ｆ(x, y)

ではあるのですが、すでに散々研究した諸々の明らかな理由で、二項関数は使わずに、単項関数としておきたいので、カリー化されている高階関数を定義します。

const plus = R => L => L + R;

高階関数の引数で、RがLより先に来ています。つまり、最初にRの値が関数適用されたら、 L => L + Rという関数が返ってくる、という構造になっています。

こういう構造になっている理由は、この順番のほうがパイプライン演算子やCustomeOperator関数その他と整合性があるからです。

const plus = R => L => L + R; 1 + 2; // 3plus(2)(1); // 3P(1)['>'](plus(2)); // 3

1 + 2 + 3; // 6plus(3)(plus(2)(1)); // 6P(1)['>'](plus(2))['>'](plus(3)) // 6

この作法に合うようにObject.defineProperty のコードを一般化すると、

const customOperator = op => f => set => Object.defineProperty(set, op, { value: function (R) { // R is Right hand side or the Binary operator return f(R)(this); // `this` is Left hand side of the Binary operator } });//returns new set/object

となります。TypeScriptでは、

const customOperator = (op: string) => (f: Function) => <T>(set: T) => Object.defineProperty(set, op, { value: function (this: object, R: <A, B>(a: A) => B) { return ((f(R))(this)); } });

利用方法は、以下の通り。

const plus = R => L => L + R; customOperator('+') (plus) (Number.prototype); (5)['+'](2) // 7(5)['+'](2)['+'](1) // 8

const minus = R => L => L - R; customOperator('-') (minus) (Number.prototype); (5)['-'](2) // 3(5)['-'](2)['-'](1) // 2

18.4. 関数合成の二項演算子の実装　グローバルパイプライン演算子（Pipeline Operator）の場合は、二項演算の対象となるオペランドがすべてのJavaScriptの値であり、Object.prototypeを触るのは流石に気が引けたので、逐一、値をPで包むというローカルアプローチで、いろいろ試した結果それで十分でした。しかし、関数合成演算の場合は、二項演算の対象となるオペランドは関数だけで、また、すべての関数には関数合成のための演算子が使えて当然だと考えるので、ローカルではなくグローバル、つまりFunction.prototypeを拡張してしまうアプローチを採用します。本稿では今後この方法をメインに活用します、 加法の二項演算の関数plusを定義したのと同様に、関数合成の二項演算の関数composeをまず定義します。 関数 f と g の合成関数は、f . g =a → a >f > gなので、

const compose = 　　g => f =>　　　　　　a => P(a)['>'](f)['>'](g) ;

あるいは、f(x)記法で、

const compose = 　　g => f =>　　　　　　a => g(f(a));

totypeにcustomeOperatorを拡張します。

customOperator('.') (compose) (Function.prototype);

TypeScriptでは、

const compose = <B, C>(g: (b: B) => C) => <A>(f: (a: A) => B) => (a: A) => g(f(a));

declare global { interface Function { ['.']: <A, B, C> (g: (b: B) => C) => ((a: A) => C) }}

使い方は以下の通り。

const compose = g => f => a => g(f(a)); customOperator('.') (compose) (Function.prototype); const f = a => a * 2;const g = a => a + 1; const fg = (f)['.'](g); // Function composition fg(5) // 11

18.5. 関数合成の二項演算子の実装　ローカルアプローチの2つ目は、パイプライン演算子（Pipeline Operator）におけるPのように、任意の関数に関数合成の二項演算子を追加するためのFを定義してやることです。 JavaScriptのコード

const F = f => "." in f ? f : Object.defineProperty(f, ".", { value: (g) => F((a) => g(f(a))) // P(a)['>'](f)['>'](g)) });

ここで、

"." in f ? f : //.....

というのは、すでにメソッド（オブジェクトプロパティ）を持っている関数に重複してObject.definePropertyをしないためです。 TypeScriptのコード

const F = <A, B>(f: (a: A) => B): F<A, B> => "." in f ? f : Object.defineProperty(f, ".", { value: <C,>(g: (b: B) => C) => F((a: A) => g(f(a))) //Function composition // P(a)['>'](f)['>'](g)) }) as any; type F<A, B> = { (a: A): B; //call signatures for js function objects ".": <C>(g: (b: B) => C) => F<A, C>;}; /* call signatures for js function objects((a: A) => B){ (a: A): B }*///https://www.typescriptlang.org/docs/handbook/2/functions.html#call-signatures

TS Playgroundで、タイプチェックの挙動が確認できます。 このローカルアプローチはもちろん機能しますが、思ったより煩雑になるので、最初のグローバルアプローチのほうを採用します。 関数の合成演算はモノイドなので、F関数を使ったローカル拡張

F(f)['.'](g)

となっているのは、結構気持ち悪くて、素直に、Function.prototypeのグローバル拡張

(f)['.'](g)

とシンプルに表現しておきたいです。 ただし、あとから実装するFRPライブラリでは、ライブラリなのでグローバルスペースに干渉するのは良くないので、自己完結しておくために、このローカルアプローチを採用しています。（どうせ関数合成は1箇所しか使っていない） 18.6. パイプライン演算子の実装どうせ” ”で囲まれるので、"|>"ではなく一番シンプルに">"をパイプライン演算子のシンボルとして割り当てることにします。

オブジェクト指向のメソッドを関数型の二項演算子として置き換えるJavaScriptで独自の二項演算子（Custom operator）を定義する Object.defineProperty( Number.prototype, "+", { value: function (R) { // R is Right hand side or the Binary operator return this + R; // `this` is Left hand side of the Binary operator }}); この場合は、オブジェクト指向的な . (ドット)記法ではSyntaxErrorになるので、代わりにプロパティ/連想配列形式でうまく書けます。 (1)['+'](2); // 3(1)['+'](2)['+'](3); // 6 と車輪の再発明

と、すでにデモンストレーションした手法を利用して

Object.defineProperty(Object.prototype, ">", { value: (f) => Object(f(x)) } );

とすればいいはずで、現代では、こういうObject.definePropertyを利用することで、オブジェクトプロパティの列挙はデフォルトで見えないようにできたり、Symbolを活用して、プロパティ名の衝突という、いわゆるオブジェクト汚染も回避できるのですが、いちおうさすがにObject.prototypeを触るのは抵抗があることと、Symbolであると演算子のシンボル名がJavaScript変数名のルールに束縛されてしまう不自由があるので、このアプローチは選択しません。 代替案として、パイプが必要なときだけ、其の場でPipeのPという名前の関数でパイプライン演算子メソッドをもつオブジェクトで包む、というアプローチを試しましたが、実際にパイプが必要なときだけ適時使う、というのはコードはさほど煩雑にならないことが判明したので結局このアプローチを選択します。18.7. null問題とオプション型（OptionType）ただしいずれのケースにおいても任意のJavaScriptの値にパイプライン演算子を実装するには、undefinedとnullの問題があります。念の為ですが、言語組み込みでパイプライン演算子を実装する際には、コードで表記されているパイプラインを既存の関数適用のして解釈しなおせばよい、SyntaxSugaarでさえあればよい、Macroでも何でも良いですが要するに単にコード上の表記に限る問題なので、何の問題もありません。そういう言語ベースでの実装ならば何の問題もないものを言語ベースでないユーザランドで実装する際に問題が出るので厄介なわけです。 nullはJavaScriptにおいて例外的で特殊なオブジェクトですがメソッドを追加できません。エラーが出ます。またundefinedもオブジェクトで包むObject(undefined)としても、{}と空オブジェクトになり、意味が異なってしまいます。 実際これはソフトウェア開発でよく知られた問題で、一般的にはヌルポインタの問題が著名です。

2009年にアントニー・ホーアは、彼が1965年にALGOL Wの一部としてヌル参照を発明したと述べている。2009年のカンファレンスでホーアはこの発明を「10億ドルの誤り」と述べた。 それは10億ドルにも相当する私の誤りだ。null参照を発明したのは1965年のことだった。当時、私はオブジェクト指向言語 (ALGOL W) における参照のための包括的型システムを設計していた。目標は、コンパイラでの自動チェックで全ての参照が完全に安全であることを保証することだった。しかし、私は単にそれが容易だというだけで、無効な参照を含める誘惑に抵抗できなかった。これは、後に数え切れない過ち、脆弱性、システムクラッシュを引き起こし、過去40年間で10億ドル相当の苦痛と損害を引き起こしたとみられる。

ただしこれは空の値をプログラミング言語がどのように実装しているか？によって別にヌルポインタに限らず問題の出方は様々で、根本的には、実装されている演算子と特殊な空の値の親和性、互換性がなく、演算が破綻する、タイプの不一致の問題です。 では、どのようなアプローチが正解か？というと、空の値であっても明示的に、その演算が対象とするオペランドの型、あるいは集合、別の言い方では、その関数の定義域に含めれば良いわけです。 このアプローチは、オプション型（Option type）としてよく知られています。

In programming languages (especially functional programming languages) and type theory, an option type or maybe type is a polymorphic type that represents encapsulation of an optional value; e.g., it is used as the return type of functions which may or may not return a meaningful value when they are applied. It consists of a constructor which either is empty (often named None or Nothing), or which encapsulates the original data type A (often written Just A or Some A).A distinct, but related concept outside of functional programming, which is popular in object-oriented programming, is called nullable types (often expressed as A?). The core difference between option types and nullable types is that option types support nesting (Maybe (Maybe A) ≠ Maybe A), while nullable types do not (String?? = String?). プログラミング言語（特に関数型言語）や型理論において、オプション型またはmay型は、オプション値のカプセル化を表す多相型である。例えば、関数を適用したときに意味のある値を返すかどうかわからない関数の戻り値の型として使用される。この型は、空であるか（NoneまたはNothingと呼ばれることが多い）、または元のデータ型Aをカプセル化する（Just AまたはSome Aと呼ばれることが多い）コンストラクタで構成されます。関数型プログラミングとは別の概念ですが、オブジェクト指向プログラミングでよく使われる関連概念として、Nullable type（しばしば A? と表記される） オプション型とヌルアブル型の主な違いは、オプション型はネストをサポートしている（Maybe (Maybe A) ≠ Maybe A）のに対し、ヌルアブル型はサポートしていない（String??? = String?）

JavaScriptにおいても、実は、オプショナルチェーン (?.) (optional chaining)なるものが実装されていて、

?. 演算子の機能は . チェーン演算子と似ていますが、参照が nullish (null または undefined) の場合にエラーとなるのではなく、式が短絡され undefined が返されるところが異なります。関数呼び出しで使用すると、与えられた関数が存在しない場合、 undefined を返します。

と、JavaScriptオブジェクトのメソッドチェーンにおいて、それなりにオプション型（Option type）の機能もネイティブに存在していることがわかります。 ただし残念ながら今回のパイプライン演算子の実装には役立たないので、素のJavaScriptの値をオプション型に拡張すると見做し、Noneというパイプライン演算子と互換性のある値を新たに添加する方針で行きます。 18.8. パイプライン演算子のコード Noneという新しい値と型、それを判別する仕組みを取り入れると、コードは相応に複雑になり、こうなります。

const customType = (type) => (set) => Object.defineProperty(set, type, { value: type });const typeNone = Symbol("None");const typeP = Symbol("P");const None = Object.defineProperty(Object(typeNone), ">", { value: (f) => P(f(None)) });const isNone = (x) => ((x === undefined) || (x === null) || (x === None));const P = (x) => (isNone(x) ? None : ((X) => !(typeP in X) && (">" in X) ? (() => { throw "'>' is used in the target Object property"; })() : (typeP in X ? X : customType(typeP)(Object.defineProperty(X, ">", { value: (f) => P(f(x)) }))))(Object(x)));

関数適用などという一番根本の部分でTypeScriptの型チェックが効いてくれないと非常に困るので、それも頑張って実装すると、さらに複雑になります。

const customType = (type: symbol) => <T>(set: T) => Object.defineProperty(set, type, { value: type }); const typeNone = Symbol("None"); const typeP = Symbol("P"); type None = undefined | null | void | typeof None; const None = Object.defineProperty( Object(typeNone), ">", { value: <B>(f: (a: None) => B) => P(f(None)) } ) as typeof typeNone; const isNone = <A>(x: A | None): x is None => ((x === undefined) || (x === null) || (x === None)); const P = <A>(x: A) => (isNone(x) ? None : ((X: P<A>) => !(typeP in X) && (">" in X) ? (() => { throw "'>' is used in the target Object property"; })() : (typeP in X ? X : customType(typeP) (Object.defineProperty(X, ">", { value: <B>(f: (a: A) => B) => P(f(x)) }) ) ))(Object(x)) ) as A extends P<unknown> ? A : (A extends None ? None : A) & P<A>; type map<A> = <B>(f: (a: A) => B) => B extends P<unknown> ? B : (B extends None ? None : B) & P<B>; type P<A> = { ">": map<A> };

TypeScript Playgroundで、実際の型の挙動が確認できます。

実際、以下のようなコード

type map<A> = <B>(f: (a: A) => B) => B extends P<unknown> ? B : (B extends None ? None : B) & P<B>; type P<A> = { ">": map<A> };

(typeP in X ? X : customType(typeP) (Object.defineProperty(X, ">", { value: <B>(f: (a: A) => B) => P(f(x)) }) )

については特別な説明が必要です。 パイプライン演算子の特徴的な型（Type）については、次の章から説明していきます。 19. ファンクタ（Functor）すべてを包括するような代数構造19.1. モノイド（Monoid）と同じくらい重要なファンクタ（Functor）という代数構造

３つの代数構造と「等しい（Equality）」という概念 「法則」であるとか「律」と書いていると面倒くさいことになった、と感じがちでなのですが、これこそが「等しい（Equality）」という超強力な概念のことなのです。ソフトウェア危機＝「本質的な複雑性」（essential complexity）＝組合せ爆発を回避する「等しい（Equality）」という超強力な概念が体系的に整理されています。いろんな代数構造が体系的に分類されているのですが、そのそれぞれにおいて、何かが「等しい（Equality）」という条件で絞り込みがなされています。本稿で気にする、扱うのはせいぜい、結合性と単位元という２つの要素だけで、双方とも、何かが「等しい（Equality）」というルールです。そして本稿で具体的に扱うのは1. モノイド（Monoid）2. ファンクタ（Functor）3. モナド（Monad）以上の、3つの代数構造だけで、これら3つともすべて二項演算の名前です。おおよそこれだけで、有向非巡回グラフ（DAG）による関数型リアクティブプログラミング（FunctionalReactiveProgramming）FRPまでカバーし、最終的には具体的なコードも示します。

モノイド（Monoid）の次に同じくらい重要な代数構造が、ファンクタ（Functor）です。

そして本稿で具体的に扱うのは1. モノイド（Monoid）2. ファンクタ（Functor）3. モナド（Monad）以上の、3つの代数構造だけで、これら3つともすべて二項演算の名前です。

と予告しているとおり、Functorも二項演算（Binary operattion）x ◦ y です。

モノイドの素晴らしさ①　型（Type）が単一の閉じた二項演算 mono- というのはモノトーンという言葉などがありますが「単一」という意味がある接頭語です。日本語でも、単系（たんけい、英: monoid; モノイド）と和訳されているようですが、あまり使わず、カタカナのモノイドです。なにが単一（モノ）なのか？というと、型（Type）が単一で、それが、S × S → Sという式で表されています。 (1 + 2) + 3 = 1 + (2 + 3)(1 × 2) × 3 = 1 × (2 × 3)で言えば、Number × Number → Number文字列結合なら、String + String → String配列結合なら、　Array concat Array → Array と扱う型（＝集合 S）が１つだけで閉じた演算です。つまり、すべて「等しい」わけです。 『銀の弾丸』等しくすれば組合せ爆発（Combinatorial explosion）を回避可能 『銀の弾などない』（No Silver Bullet ）というのは誤りで、『銀の弾』は実は存在していて、それは「等しい（Equality）」という超強力な概念に他なりません。ソフトウェア開発、あるいはプログラミングにおける「本質的な複雑性」（essential complexity）とは、ほんとうは数学的な概念で、それは、組合せ爆発（Combinatorial explosion）です。 組合せ爆発（くみあわせばくはつ、英: combinatorial explosion）は、計算機科学、応用数学、情報工学、人工知能などの分野では、解が組合せ（combination）的な条件で定義される離散最適化問題で、問題の大きさn に対して解の数が指数関数や階乗などのオーダーで急激に大きくなってしまうために、有限時間で解あるいは最適解を発見することが困難になることをいう。 念の為ですが、解決したい課題の対象が本質的に原理的に内在している組み合わせ爆発のことではなく、プログラマが書いてしまいがちで、不注意な、あるいは、不適切な工学的アプローチによるコード自体が本質的には回避可能であるのにもかかわらず、非合理的に、無用に、組みわせ爆発を起こしている、ということです。無用な組合せ爆発を回避するためには、可能な限り要素を減らすこと、そして何より肝要なことは、本質的に等しいものは、等しいものとして徹底的に扱うこと、さらに必ずしも等しくなければならない要請はなくても、等しいものとして扱うことができるならば等しくする、ということです。要素が1つしかなければ、組み合わせというのが原理的に存在しないので、組合せ爆発による問題など起こりようがありません。しかし、それぞれの要素に区別があるときは、指数関数的に組み合わせ爆発が起こり収集はつかなくなります。数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないのですが、裏を返すと「唯一正しい工学的アプローチ」『銀の弾丸』とは、組合せ爆発を回避する「等しくする」という数学的アプローチです。 モノイドはまさに要素が1つしかなければ、組み合わせというのが原理的に存在しないパターンに該当していて、本質的な複雑性である組合せ爆発を回避できる非常に安全な代数構造です。 モノイドは工学的な観点からみると、工業規格と同じです。 数学の範疇外での余剰の工学的発明は複雑さの元凶でしかないのですが、裏を返すと「唯一正しい工学的アプローチ」『銀の弾丸』とは、組合せ爆発を回避する「等しくする」という数学的アプローチです。実際これはソフトウェア開発に限らない一般的な工学的な問題として死活問題なので、工業規格という人類の経験則による知見が存在しています。ISO規格（国際標準化機構）があり、JIS（日本）など各国に規格が決定されています。 身近なところでは、電気のコンセントプラグがあり、特にプログラマにとっては、USB規格があります。 ユニバーサル・シリアル・バス（英: Universal Serial Bus、略称：USB、ユーエスビー）は、コンピュータ等の情報機器に周辺機器を接続するためのシリアルバス規格の1つ。ユニバーサル（汎用）の名の示す通り、ホスト機器にさまざまな周辺機器を接続するためのペリフェラルバス規格であり、最初の規格となるUSB 1.0は1996年に登場した。現在のパーソナルコンピュータ周辺機器において、最も普及した汎用インターフェース規格である。 もちろん、Appleのように独自の規格、つまり自前機器のエコだけで完結すれば良いだろう、というのもひとつの主張ではありますが、最近排除されて消費者に歓迎された事案は記憶に新しいところです。EU スマートフォンの充電器をUSB Type-Cへ統一へ（iPhoneのLightningケーブル排除へ） USBなどを使っているとわかりますが、こういう「等しさ」が担保されている概念はBuilding blockになります。その定められた規格内に収まってさえおれば、それらは「等しい」と見做され、自由自在に組み合わせても壊れる心配がありません。LEGOもそれ自体がBuilding blockであり単一の接続規格で、自由自在に構築可能です。 根源的には、コードの要素を等しく保つというアプローチで、コードをUSBデバイスやLEGOブロックのように自由自在に組み合わせてもコードは壊れないと担保される、バグのでないメンテナンス性の高いコードをプログラミング可能となります。

と示したとおり、モノイドは極めてシンプルな単一タイプの代数構造で、同じタイプのブロックを安全に連結できて、プログラミングのコードをレゴブロック、USBのように構築できる、というものすごいアドバンテージがあるわけですが、逆にシンプルすぎて、このモノイドだけでは関数コードを記述しきれません。 19.2. ファンクタ（Functor）すべてを包括するような代数構造 それというのも、そもそも、情報処理、プログラミングとは原理的に、

型理論（Type theory）	型（type）	関数（function）/ 写像（map）
集合論（Set theory）	集合（set）始集合（domain）と終集合（codomain）	写像（map）
解析学（Analysis）	定義域（domain）と値域（range）と終域（codomain）	関数（function）
代数学（Algebra）	集合（set）/ 被演算子（operand）	演算子（operator）
オブジェクト指向（Object-oriented programming）	オブジェクト（object）	メソッド（method）
圏論（Category theory）	対象（object）/ 圏（category）	射（morphism）

情報処理・プログラミング

データ（data）

処理（operation）

このような構造になっています。 そして、この図そのものがFunctorの概念を表しています。 つまり、Functorは二項演算で、演算子（オペレータ）と左右のオペランドがあるわけですが、• 左オペランドは、この図の左側• 右オペランドは、この図の右側 図の左右では、明らかにタイプが異なります。だから単一タイプのモノイドでは役不足であるということになります。 図をさらに詳しく見ると、• 左オペランドは、型＝集合• 右オペランドは、関数になっています。 したがって、Functorという代数構造は、 A をある型（Type）（=集合)f を関数（Function）（の集合）・ を二項演算子（Binary operator）とすると、 A ・ f と表現できる二項演算です。 これが、

要するに、関数そのもので議論したりコードに書き込むよりも、二項演算として表記したほうが圧倒的にコードが簡単になり、直感的に理解が可能で、見通しがよくなりメンテナンスが楽になる、つまりバグが紛れ込むリスクが激減するというとてつもないメリットがあるので、二項演算のほうを採用したい、そして、関数型プログラミングでは、二つの演算によって決まる代数的構造、つまり二項演算だけで、ほぼほぼ事が足りてしまうのです。

と書いた意図そのものです。Functorという二項演算で全部カバーできてしまう。

となっているので、いわゆる循環論法というか自己言及になっていますが、演算子というものは根源的には、関数（function）/ 写像（map）であるので、そう読み替えると別に問題はないです。そして、実際にこのようにどんどん抽象度があがっていくにつれて、演算子と関数が相互にコロコロと立場を変えるようなことことが起こってきます。 これが一番外側のアウトラインの説明で、Functorという代数構造は、情報処理、プログラミングのコードを書くとき、かなり包括的かつ根源的で極めて重要な代数構造である、と言えます。 19.3. Array.map()というファンクタ（Functor）を調べればわかってくること 一番外側のアウトラインを理解したところで、身近で具体的な事例を研究します。 Array.prototype.map()については、

map() メソッドは、与えられた関数を配列のすべての要素に対して呼び出し、その結果からなる新しい配列を生成します。

と、Arrayオブジェクトの便利なメソッドとして紹介されており、その使い方がひたすら解説されているだけで、その素性が解説に含まれていることはほぼありません。JavaScriptがオブジェクト指向言語として世に広まった一つの弊害ではあるでしょう。

既存のオブジェクトメソッドを二項演算子として捉え直す 上記のとおり、オブジェクトメソッド表記が、オブジェクトプロパティ/連想配列形式で表記できる、というのは、逆方向に応用することも可能です。つまり、 array1.concat(array2);array1['concat'](array2); と書き直せるということで、すでに確認したとおり、 オブジェクト指向のオブジェクトは、数学の集合(Sets)に相当し、二項演算の左側の被演算子（Operand）になります。オブジェクト指向のメソッドは、数学の二項演算子(Binary operatior)に相当しており、オブジェクト指向のメソッドの引数（Parameter）は、二項演算の右側の被演算子（Operand）になります。 という事実が、オブジェクトメソッド表記から一旦離れることにより、意識しやすくなります。もちろん、既にオブジェクトメソッド表記で簡潔に書けていることは間違いないので、無理に書き直す必要性はないでしょうが、あくまで二項演算子として扱うことを常に意識するためには役立つでしょう。 同様の原理で、Arrayオブジェクトには最初から.mapメソッドが実装されていることを考慮して、 const f = a => a + 1; [1, 2, 3].map(f); // [2, 3, 4][1, 2, 3]['map'](f); // [2, 3, 4] というように、Array.map(f) メソッドというのは、配列Arrayと関数f との間の二項演算子 map である、と理解できます。 • 'map' は、ArrayとFuncttionからArrayを生み出す二項演算子です。• Array 'map' Function = Array• [1,2,3] ['map'] (f) = [2,3,4]

ということなのですが、基本的にArray.mapメソッドは二項演算子であり、根本的には関数です。二項関数であるともいえますが、カリー化されている単項関数にすれば、より詳しく調べることができます。つまり、加法の二項演算について、plus(1, 2) = 3

const plus = (L, R) => L + R;

ではなく、

const plus = R => L => L + R; customOperator('+') (plus) (Number.prototype); (5)['+'](2) // 7(5)['+'](2)['+'](1) // 8

とやったことの繰り返しをします。 Array.mapから、純粋にmap関数だけを抽出すると、

const map = f => A => A.map(f);

こうなります。plusという単項の高階関数の構造と見比べると、

const plus = R => L => L + R;

同じ構造であることがわかるはずです。＋が二項演算子であるのと同じで、mapメソッドはオペランドであるAとfの間にある二項演算子です。 そして、ここから、

const map = f => A => A.map(f); customOperator('map') (map) (Array.prototype);

とすると、エラーになります。なぜならば、すでに存在するArray.prototype.map()から、mapを抽出して定義したので、その同じmapを再びArray.prototypeに上書きしようとしてしまったからです。

const plus = R => L => L + R; 1 + 2; // 3plus(2)(1); // 3P(1)['>'](plus(2)); // 3

と書けたのと同じように、

const map = f => A => A.map(f); const f = a => a + 1; P([1, 2, 3])['>'](map(f));// [ 2, 3, 4 ]

と書けます。 より純粋に数式で書くと、[1,2,3] > map( f )となっており、これは、オブジェクト指向のメソッド記法

[1, 2, 3].map(f)

と構造が同じであることが確認できます。 パイプライン演算子のおかげで、このようにオブジェクトメソッドと関数型コードとのつながりが明白になりました。 つまり、「本来のシンプルなありかた」としては、map関数をなにもないところから定義して、パイプライン演算子で[1,2,3]という左オペランドf という右オペランドの二項演算を構成するというやり方で十分で、わざわざArrayオブジェクトの標準メソッドとして提供されるのを待っている、ES20XXでは、便利なメソッドが新たに追加された、であるとか、そういうアプローチは不自然であるし、不要です。あるいは、クラスを設計してメソッドを組み込む、という大掛かりな作業も本当は必要はありません。 オブジェクトのメソッドチェーンにしても、それは結局の所、二項演算の連鎖ですから、同様に実現できます。 そして重要なことは、

A.map(f)

あるいは

A['map'](f)

と書ける二項演算であるmapは、まさに、

Functorという代数構造は、A をある型（Type）（=集合)f を関数（Function）（の集合）・ を二項演算子（Binary operator）とすると、A ・ fと表現できる二項演算です。

というパターンにあてはまっていて、mapはFunctorです。 さらに、mapを高階関数としてきちんと分離しておくと、[1,2,3] > map( f )

const map = f => A => A.map(f); const f = a => a + 1; P([1, 2, 3])['>'](map(f));// [ 2, 3, 4 ]

と書けます。　 19.4. パイプライン演算（Pipeline operation）は Identity functor

A['map'](f)

と書ける二項演算であるmapは、まさに、

Functorという代数構造は、A をある型（Type）（=集合)F を関数（Function）（の集合）・ を二項演算子（Binary operator）とすると、A ・ Fと表現できる二項演算です。

というパターンにあてはまっていて、mapはFunctorというのであれば、

A['>'](f)

と書ける二項演算であるパイプライン演算（Pipeline operation）もFunctorでしょう。 [1,2,3] > map( f )

const map = f => A => A.map(f); const f = a => a + 1; P([1, 2, 3])['>'](map(f));// [ 2, 3, 4 ]

のかわりに、1 > identity( f )

const identity = f => f; const f = a => a + 1; P(1)['>'](identity(f));// [Number: 2]

と書くことができます。 そして、identty関数というのは素通りする関数で、identity(f) = f

const identity = f => f; const f = a => a + 1; identity(f) === f // true

なので、簡略化して、1 > f

const f = a => a + 1; P(1)['>'](f); // [Number: 2]

つまり、パイプライン演算、これは関数の適用 f(x) であるのですが、Functor である、ことがわかります。特に、Identity functorと呼ばれ、もっとも基本的なFunctorです。 19.5. FunctorはIdentity functor（関数適用）を基本とする拡張可能な代数構造 Functorは、普通の関数適用まで包括している根源的な代数構造であることが確認できました。

ファンクタ（Functor）すべてを包括するような代数構造 それというのも、そもそも、情報処理、プログラミングとは原理的に、 型理論（Type theory） 型（type） 関数（function）/ 写像（map） 集合論（Set theory） 集合（set）始集合（domain）と終集合（codomain） 写像（map） 解析学（Analysis） 定義域（domain）と値域（range）と終域（codomain） 関数（function） 代数学（Algebra） 集合（set）/ 被演算子（operand） 演算子（operator） オブジェクト指向（Object-oriented programming） オブジェクト（object） メソッド（method） 圏論（Category theory） 対象（object）/ 圏（category） 射（morphism） 情報処理・プログラミング データ（data） 処理（operation） このような構造になっています。そして、この図そのものがFunctorの概念を表しています。つまり、Functorは二項演算で、演算子（オペレータ）と左右のオペランドがあるわけですが、• 左オペランドは、この図の左側• 右オペランドは、この図の右側図の左右では、明らかにタイプが異なります。だから単一タイプのモノイドでは役不足であるということになります。図をさらに詳しく見ると、• 左オペランドは、型＝集合• 右オペランドは、関数になっています。したがって、Functorという代数構造は、A をある型（Type）（=集合)f を関数（Function）（の集合）・ を二項演算子（Binary operator）とすると、A ・ fと表現できる二項演算です。

というのは、もっと正確には、A ・ fではなくて、パイプライン演算=関数適用f(x)を基本とした、A > fあるいは、A > identity(f)で、これが通常の関数適用 f(x) の世界の範囲になっている、さらにそこから、「何もしない」identity関数の代わりに「何か構造をもつ」map関数に置き換えることで、A > map(f)と二項演算をいくらでも高機能化するように拡張可能、それがFunctorという代数構造である、と理解できます。 19.6. Functorをもっと厳密にTypeScriptで定義していくそもそもが、Functorとは。• A をある型（Type）（=集合)• f を関数（Function）（の集合）というような、型（Type）の構造の話であって、我々にはその型を明示できるTypeScriptがあるので、FunctorをTypeScriptをもって定義していきます。その作業によってよりわかってくることがあるでしょう。 ちなみにですが、Functorを定義する際に、巷の関数型プログラミングの解説で多いのが、というかほとんどがそのパターンなのですが、オブジェクﾄ、JSON、それから一番最悪なのが、ES6以降のクラス（Class）をもって定義しているコードです。 関数型のコードで、そういう水と油というか別パラダイムの道具立てを借りて、Functorというようなかなり根源的な代数構造をほら定義できました的に披露されるのは、非常にストレスですし、何かごまかされているような気になります。 ある程度はJSONにしても「構造体」という抽象概念としての利用はしますが、必要がなければ使いたくはないですし本質から目をそらしやすい障害になりかねません。 そこで、本稿では、JavaScriptの配列（Array）を利用します。配列（Array）はかんたんで、ほぼすべてのプログラマーにとって馴染み深く、その構造が直接可視化しやすいこと、それからArray.map() などすでに使い倒しているメソッド、関数と親和性が高いので、うってつけです。 まず準備段階として、基本の基本から触っていくと、 1 > identity( f )

const identity = f => f; const f = a => a + 1; P(1)['>'](identity(f));// [Number: 2]

というコードを書きました。これが、Identity functorと呼ばれていて、もっとも基本的なただの関数適用のFunctorなのでした。 Identity関数は

const identity = a => a;

と書けば、なんということはないのですが、入ってくる値のタイプが、関数fであるときは、

const identity = f => f;

様子が異なります。 インプットが関数アウトプットが関数の高階関数となっているのです。 その様子を簡略化した数式で表現すると、identity: f→f identity: (a→b)→(a→b) 後者のほうがより高階関数の構造が明示されています。 実際に、TypeScriptで型をつけると、

const identity = <A>(a: A) => a;

const identity = (f: <A, B>(a: A) => B) => f;

これがより複雑な構造をもつmapに置き換えられるFunctorでは、map: (a→b)→([a]→[b])となりますが、プレースホルダのシンボルの種類が増えてきたので、一旦仕切り直して、

Functorという代数構造は、A をある型（Type）（=集合)f を関数（Function）（の集合）・ を二項演算子（Binary operator）とすると、A ・ fと表現できる二項演算

というのを

[A] map f = [B]と表現できる二項演算

とまとめます。 TypeScriptで型をつけると、A→B という関数で　その関数を表す小文字の f や aはプレースホルダにすぎないことに留意して、A[] → B[] という関数で、小文字を含むFaもプレースホルダにすぎないことに留意して、

type map = <A, B> (f: (a: A) => B) => (Fa: A[]) => B[];

となります。 今、二項演算子を構成する関数を定義しようとしていているのですが、ある型（Type）（=集合)というのは、そんなどこからともなく湧いてくるわけもなくて、そもそも二項演算というのは、集合と二項演算子のペアですから、こちらもきちんと定義しておく必要があります。 今は、かんたんな配列なので、[]でくくるだけで暗黙のうちにそのArray型を生み出しているわけです。きちんと明示しておくと、単純に、

const F = // type constructor a => [a];

となります。こういう何もないところから、ある特別な型（Type）を新規に構築する（生み出す）関数のことを、型構築子/タイプコンストラクタ（Type constructor）といいます。オブジェクト指向でいうところの、コンストラクタ（Constructor）に該当します。 TypeScriptにおいてはタイプコンストラクタにも当然きちんと型（Type）がつくのですが、ジェネリックを使って、以下のようにタイプ定義します。

type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a];

素の値であるAから、タイプコンストラクタであるFによって　F<A>という新しい型（Type）が新規に構築された（生み出された）様相がうまく表現されています。 これは直感的にもわかりやすく美しい表現ですし、配列に限らず他の全ての型にも一貫して応用できるので、A[]やB[]と書く代わりにF<A>F<B>と書いてしまって、

type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0]));

const f = (a: number) => a * 2; const A = F(1); // [1] type constructconst B = P(A)['>'](map(f));// [2] mapped

このコードでは概念をかんたんに示す目的のために「1要素だけの配列のmap」を定義しています。 型定義だけを改めて抜粋すると、

type F<A> = A[]; // type constructor type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>;

このTypeScriptのコードで、かなり正確に、Functorの概念を表現できています。 ちなみに、Haskellでは、型定義にプレースホルダは積み増さない流儀なので、

fmap :: (a -> b) -> f a -> f b

とFunctorはよりスッキリと定義されてるのですが、全く同じ意味です。 TypeScriptではプレースホルダは逐一明示したほうが便利だ、という方針で、そのメリットは確かに大きいですが、こういう抽象度が高い概念になると、逆に見通しが悪くなるデメリットはありますね。 視覚的に表現するとこういう概念図になるでしょう。

mapFunctorfmap(f)FunctionFunctionmorphismmorphism19.7. 圏論（Category theory）のFunctor そもそも、Functorとは圏論（Category theory）で定義された概念なのですが、nLabのFunctorの項目によると、

この図をみると、ちょうど、

(f: (a: A) => B) => (Fa: F<A>) => F<B>

というコードの表現がそのまま書かれていることが感じられると思います。 あとの矢印と字面については、要するに、新しい型（Type）、これは圏論では「圏（Category）」に該当するわけですが、その世界でも、関数の合成（Function composition）を維持しなければならない、という圏論におけるFunctorの定義上の要請です。

const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0]));

の一番最後に、再びF関数というタイプコンストラクタに入れてしまって、配列（Array）に戻しているので、インプットとアウトプットのタイプは同一になります。配列をmapしても配列になっている、つまり接続が保証されており、連鎖できるような構造です。関数の合成（Function composition）は、関数が連結さえすれば自然と出てきた概念で必ず成立するので、この定義上の要請は自動的に満たしています。 こういう、インプットとアウトプットのタイプが「等しい」ことが保証されているFunctorのことを特別にendo-Functorと呼びます。そして関数型コードで扱うのはendo-Functor一択で、特に断りのない限り関数型プログラミングでFunctorというときは、暗黙の了解のように、endo-Functorつまりこういうmapやらパイプライン演算のことを指定しています。 そもそも圏論（Category theory）は、関数合成やFunctorのことを研究するためにはじめられた学問であり、本稿ではすでにその要点はきっちりと抑えた、ということになります。 こと圏論においてはWikipediaの項目はあまり役に立たないのですが、 関手（Functor）

圏論における関手（かんしゅ、英: functor）は、圏から圏への構造と両立する対応付けである。関手によって一つの数学体系から別の体系への組織的な対応が定式化される。関手は「圏の圏」における射と考えることもできる。

というのは、要するに上のnLabの引用、図と同じ意味のことを言及しています。 　 20. モナド（Monad）はファンクタ（Functor）の特別なケース 20.1. パイプライン演算は関数合成（Function composition）ができる パイプライン演算は関数の適用 f(x) であるのですが、Identity functorと呼ばれるもっとも基本的なFunctorであることは理解できました。 そして、パイプライン演算/Identity functor/関数の適用では、関数の合成（Function composition）ができます。

関数（写像）の連鎖の例にふたたび注目します。 346ABC+1+2+3346+1+2+3　　ここで、関数（写像）はf: +1g: +2と２つあって、写像が連鎖した結果、f.g: +3という関数合成ができているということでした。 どうしても、必要、というわけでもないですが、全く同じグラフを 346+1+2+3 このように、トライアングルにすることができます。 まずデメリットは、いきなりこのグラフを示されると、最初の数直線的なグラフのイメージが湧きにくいことがあります。メリットは、まず f.g: +3 の合成関数が曲線で書かなくてすむことや、また、そもそも関数というのは、+1,+2というような数直線上に並ぶ四則演算とは限らないので、より抽象的な操作ぽいこと、それから後々わかりますが、このほうがスペースを効率的に使っており、あとからグラフを追加しやすい、ことなどがあるでしょうか。 そのとおり、より抽象的に表現すると、 ABCfgf⋅gf:A→Bg:B→Cf⋅g:A→C a> f⋅g =a>f > g =c これが、関数 f と g と合成された関数である f.g の一般的なイメージとして使えます。

関数（写像）合成（Function composition）は二項演算 f と g という2つの関数（写像）の合成というのは、f と g という2つの関数の間の二項演算 f . g であると捉えることができます。ここで、.　は二項演算子です。 パイプライン演算子（Pipeline Operator）を活用して、3 > f > g P(3)['>'](f)['>'](g)　　// 6 と表現して、さらに、a > f >g = a > (f . g)fg = f.g3 > fg3 > (f.g) const fg = f['.'](g);P(3)['>'](fg); // 6P(3)['>']( f['.'](g) ); // 6 となるような関数合成の二項演算子を定義することができます。

そして、

写像の合成は、二項演算であり、それが定義される限りにおいて常に結合的ということは、要するに写像の連鎖が成立している限り、常に結合性がある半群（Semigroup）であり、半群には必ず単位元がいつでも追加できるのは保証されているので、関数（写像）の合成はモノイドです。

(f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)id ⋅ f=f=f ⋅ id

さらに、なんで結合性があってモノイドになると良いのか？というとレゴブロックのように、あらゆる組み合わせ順序の結果が等しくなるからですね。

極めて重要なことなので念の為に繰り返しますが、関数合成という関数型プログラミングで極めて根本的な二項演算において、結合性があること、 括弧をつける位置の選び方は写像の合成の結果に影響を及ぼさないということを意味しているから、括弧を取り除いても意味を損なうことは無く、しばしば括弧を省略して f ⋅ g ⋅ h と書かれる。写像の数がさらに増えても同様である。 (f⋅g)⋅h=f⋅(g⋅h) が成立しているということは、グルーピング演算子（）の位置は気にする必要がなく（）をつけてもつけなくても「等しい」ことf ⋅ g ⋅ h が保証されているわけですから、組み合わせ爆発の危険性がない、安全な代数構造である、ということを意味しています。

20.2. パイプライン演算はIdentity functorで関数合成（Function composition）ができる特別なFunctor モナド（Monad） パイプライン演算は関数の適用 f(x) であるのですが、Identity functorと呼ばれるもっとも基本的なFunctorであり、かつ関数の合成（Function composition）ができます。 パイプライン演算a > f はFunctorで、当たり前のことですが単一タイプであるMonoidではありません。(a>f)>g ≠ a>(f>g)しかし、このようにある二項演算の合成の演算がモノイド（Monoid）を構成しているとき、

(f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)id ⋅ f=f=f ⋅ id

その二項演算をモナド（Monad）と呼びます。 そして実は、Functorの世界では、こういう自然に、自動的に、関数合成できて、それがMonoidという安全な代数構造だ、というのは、Identity functorだけ、なんですね。特別なのです。 理由はシンプルで、Identity functorのタイプコンストラクタが、まさにIdentity関数

const identity = // type constructor a => a;

であり、普通に考えてみるとわかりますが、5であるとか"Hello"という、値がIdentity functorのタイプコンストラクタ、つまりIdentity関数を通ってFunctorの型（Type）になった後でも、そのまま変わらない、つまり内部構造をもっていない、からです。 他方で、配列（Array）のmapFunctorのタイプコンストラクタでは、

const F = // type constructor a => [a];

と、そもそもがなにか特別な構造をもたせるように、新しいFunctorの型（Type）を生み出しているわけです。原理的に、Identity functor以外のすべてのFunctorがそうなっています。ここで原理的にIdentityの「等しい」という性質がひとつ損なわれてしまっているので、その分だけきっちりと複雑性が追加されていることになります。 これが、直感的な、Functorの世界では、こういう自然に、自動的に、関数合成できて、それがMonoidという安全な代数構造だ、というのは、Identity functorだけという理解です。一番外側のアウトラインの説明です。 Identity functorはMonad（モナド）でもあるので、Identity monad（恒等モナド）と呼ばれます。 Identity monad 恒等モナド 上記の

というのは、本稿でx > f = f(x)パイプライン演算 = 関数適用と書いているのと同じです。 20.3. mapFunctorの連結の様子 Functorの合成（composition）では、実際に身近なArray.map()で検証してみましょう。mapFunctorです。 Identity functorあるいはIdentity monadである、パイプライン演算では、以下のように関数合成（Function composition）ができます。これは素朴に関数の連結のことです。

346+1+2+3 関数型コードでは、こういうなっています。

パイプライン演算子（Pipeline Operator）を活用して、3 > f > g P(3)['>'](f)['>'](g)　　// 6 と表現して、さらに、a > f >g = a > (f . g)fg = f.g3 > fg3 > (f.g) const fg = f['.'](g);P(3)['>'](fg); // 6P(3)['>']( f['.'](g) ); // 6

この f と g は、+1と+2の関数です。

const f = a => a + 1;const g = a => a + 2;

この関数を共有して、mapFunctorの挙動を研究してみましょう。

[3][4][6]map(+1) map(+2)map(+3) Functorの連鎖

[3].map(f).map(g) // [6]

連結されたFunctor

const fg = f['.'](g); // +3[3].map(fg) // [6][3].map(f['.'](g)) // [6]

これは成立しています。この事実がまさに、関数の合成（Function composition）を維持しなければならない、という圏論におけるFunctorの定義上の要請で、Functorの連結、あるいは、Functorの合成（Functor composition）と言えます。

圏論（Category theory）のFunctor そもそも、Functorとは圏論（Category theory）で定義された概念なのですが、nLabのFunctorの項目によると、 この図をみると、ちょうど、 (f: (a: A) => B) => (Fa: F<A>) => F<B> というコードの表現がそのまま書かれていることが感じられると思います。 あとの矢印と字面については、要するに、新しい型（Type）、これは圏論では「圏（Category）」に該当するわけですが、その世界でも、関数の合成（Function composition）を維持しなければならない、という圏論におけるFunctorの定義上の要請です。 const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0])); の一番最後に、再びF関数というタイプコンストラクタに入れてしまって、配列（Array）に戻しているので、インプットとアウトプットのタイプは同一になります。配列をmapしても配列になっている、つまり接続が保証されており、連鎖できるような構造です。関数の合成（Function composition）は、関数が連結さえすれば自然と出てきた概念で必ず成立するので、この定義上の要請は自動的に満たしています。 こういう、インプットとアウトプットのタイプが「等しい」ことが保証されているFunctorのことを特別にendo-Functorと呼びます。そして関数型コードで扱うのはendo-Functor一択で、特に断りのない限り関数型プログラミングでFunctorというときは、暗黙の了解のように、endo-Functorつまりこういうmapやらパイプライン演算のことを指定しています。

で、関数型プログラミングの範囲では、endoFunctorを普通に実装している限りは自動的に成立するので気をもむ必要はないですが、Functor則（Functor law）などと言う言葉で大上段から解説されることが多く、多くの場合意味がわからないでしょうし、わかったつもりになることはできます。 ここで、表記というのは非常に重要なので、理解しやすいようにmapというmapFunctorの二項演算子を≫に置き換えます。identityFunctorであるパイプライン演算子が>なので、より複雑なFunctor一般、というイメージです。 identityFunctorであるパイプライン演算では、

346+1+2+3 3 > f >g = 3 > (f . g)という関数合成でしたが、mapFunctorでは、

[3][4][6]map(+1) map(+2)map(+3) Functorの連鎖

[3].map(f).map(g) // [6]

合成された関数のFunctor

const fg = f['.'](g); // +3[3].map(fg) // [6][3].map(f['.'](g)) // [6]

のmap 二項演算子を≫　に置き換えて、[3] ≫ f ≫ g = [3] ≫ (f . g)ということが成立しています。 20.4. mapFunctorの合成（Functor composition）の問題点 ところがよくよく考えてみると、f . gというのは、関数の合成、つまりidentityFunctorであるパイプライン演算による関数の合成（Function composition）です。f . g =a → a >f > g これで置き換えてみると、[3] ≫ f ≫ g = [3] ≫ (a → a >f > g)となっており、異なる二項演算子が混ざっている事が確認できます。 identityFunctorであるパイプライン演算による関数の合成では、当然、二項演算子は、パイプライン演算子ひとつだけに統一されています。3 > f >g = 3 > (a → a >f > g)この事実は結構重大で、やはり「等しい」ことが安全な代数構造で、安全なコーディングができる、という原理原則になってきます。裏を返すと、

ある二項演算の合成の演算がモノイド（Monoid）を構成しているとき、 (f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)id ⋅ f=f=f ⋅ id その二項演算をモナド（Monad）と呼びます。 そして実は、Functorの世界では、こういう自然に、自動的に、関数合成できて、それがMonoidという安全な代数構造だ、というのは、Identity functorだけ、なんですね。特別なのです。

ということを反映していて、「単一の演算子で関数合成が自然に成立しており、それは自動的に結合性があることになり（）の組み合わせを気にする必要がないMonoidで、そういうIdentityFunctorはMonadと呼ばれている」ということは、mapFunctorでは自動的に成立なんてしていない、ということを意味します。 3 > f >g = 3 > (a → a >f > g)というのと同じように、mapFunctorであっても、もし、 [3] ≫ f ≫ g = [3] ≫ (a → [a] ≫f ≫ g) と二項演算子　≫で、統一されるのであれば、それはmapFunctorでも、identityFunctorの関数合成と同じように、mapFunctorの合成ができるようになる、Monadになる、ということです。 あと、細かいことで混乱しやすいのですが、 (a → [a] ≫f ≫ g)というように、二項演算の頭に、タイプコンストラクタである[a]が必要です。identityFunctorであるパイプライン演算では必要なかったのですが、 (a → a >f > g) (a → identity(a) >f > g)と、二項演算の頭に、identityFunctorのタイプコンストラクタであるidentity関数が暗黙に存在している、と考えれば、整合性がつきます。 そしてまさにこの差の複雑性の増加により、identityFunctor以外のFunctorでは自然と単一の演算子で合成ができずMonadになっていない、と考えられます。 実際に[3] ≫ f ≫ g = [3] ≫ (a → [a] ≫f ≫ g)であると仮に想定しながら、試しにArray.map()を使って実験してみると、

[3].map(a => [a].map(f).map(g))　// [[3]]

と[3]ではなく、[[3]]となってしまっています。 mapFunctorのタイプコンストラクタである、[a]が二重に適用されてしまった結果です。 これがもしidentityFunctorのタイプコンストラクタである、identity関数　a → aならば二重に適用されても構造は変わりません。最初から内部構造がない、とも言えます。安全な代数構造です。 実際に、リアル世界のコードで、このように、mapメソッドチェーンを使い倒していて、ある式を、再利用可能な関数として切り出して、別のmapメソッドチェーンに組み入れる、関数の切り貼りのシナリオは普通にありえます。 そこで「関数なので自動的に連結（関数合成）してくれるのだろう」と安心していたら、なんか[[]] と二重の入れ子構造になったデータが出てきた!!原因は不明だ？？というバグが発生しかねません、ということはタイムスパンはわからないですがそのうち必ず発生するでしょう。原因不明の安全でない代数構造を放置して、それに気がつかないままコーディングをしているのだから。 これは、解決すべき重要な問題です。Array.map()はモナド（Monad）ではありません。 20.5. flatMapMonadの登場 　　この問題はある一定以上のレベルの関数型プログラマの間では認識されていて、その結果、ES2019で新たに実装された、Array.flatMap() メソッドがモナド（Monad）です。 https://github.com/tc39/proposal-flatMap/issues/10

This proposal essentially gives native Arrays the methods they need to work as Monads (without having to extend the prototype).

Array.flatMap() メソッドを利用して

[3].map(a => [a].map(f).map(g))　// [[3]]

と同じ実験をしてみると、

[3].flatMap(a => [a].flatMap(f).flatMap(g))　// [3]

[3] ≫ f ≫ g = [3] ≫ (a → [a] ≫f ≫ g)が想定通り、成立しました。 20.6. mapとflatMapの比較

map(f)map(g)map(f)·map(g) = map(f·g) f gf·g a [a]a > f > g=a > (f·g)[a] > map(f) >map(g)=[a] > (map(f)·map(g))=[a] > map(f·g)[a] map f map g=[a] map (f·g)=[a] map (a → a > f > g)≠[a] map (a → [a] map f map g)=[a] map (a → [a] map (f·g))flatMap(f)flatMap(g)flatMap(f)·flatMap(g) = flatMap(f·g) [a][a] > flatMap(f) >flatMap(g)=[a] > (flatMap(f)·flatMap(g))=[a] > flatMap(f·g)[a] flatMap f flatMap g=[a] flatMap (f·g)=[a] flatMap (a → a > f > g)=[a] flatMap (a → [a] flatMap f flatMap g)=[a] flatMap (a → [a] flatMap (f·g)) =[a] flatMap(f•g)mapで赤で表示されている部分が、プログラマが間違って＝だと見做してしまう可能性がある箇所です。flatMapでは青に表示されている通り、直感通りの挙動を示し、＝（等しくなり）、複雑性が排除されています。

実際に、リアル世界のコードで、このように、mapメソッドチェーンを使い倒していて、ある式を、再利用可能な関数として切り出して、別のmapメソッドチェーンに組み入れる、関数の切り貼りのシナリオは普通にありえます。

20.7. flatMapは結合性と単位元があるFunctorなのでMonad identityFunctorがidentityMonadであったように、flatMapFunctorはflatMapMonadである、といえます。 関数の合成が成立したことによって自動的に結合性もある

写像の合成（Function composition） 写像の合成は、それが定義される限りにおいて常に結合的である。すなわち、f, g, h がそれぞれ（合成が定義できるように）適当に選ばれた始域および終域を備えた写像であるとするならば、 が成り立つ。 ここで、括弧はそれが付いているところから先に合成を計算することを指し示すためのものである。これは括弧をつける位置の選び方は写像の合成の結果に影響を及ぼさないということを意味しているから、括弧を取り除いても意味を損なうことは無く、しばしば括弧を省略して f ⋅ g ⋅ h と書かれる。写像の数がさらに増えても同様である。 写像の合成は、二項演算であり、それが定義される限りにおいて常に結合的ということは、要するに写像の連鎖が成立している限り、結合性がある半群（Semigroup）であり、半群には必ず単位元がいつでも追加できるのは保証されているので、写像の合成はモノイドです。

+5+3+3+2+19643 Dとhを付けて h:C→Dg⋅h:B→D g⋅hf⋅ghgfDCBA(f⋅g)⋅h=f⋅(g⋅h) 関数合成という二項演算は、連鎖が成立している限り必ず結合性があるのがわかります。

従って、半群（Semigroup）です。そして、半群（Semigroup）であるならば、

半群（Semigroup）にはいつでも単位元を追加してモノイドにできる

ということでした。

(f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)id ⋅ f=f=f ⋅ id

20.8. Monadの左右の単位元（Identity）はタイプコンストラクタ関数 そして、Monadにおいては、この左右の単位元 id というのは、必ず、タイプコンストラクタ関数になります。 この非常に興味深い事実を検証してみます。 id ⋅ f=f=f ⋅ id mapFunctor / mapMonad のタイプコンスタクタid = a => [a]

const id = a => [a];

とし、関数 f

const f = a => id(a * 2);

とのFunctorの合成の二項演算を試行します。　ここで、関数 f が、

const f = a => a * 2;

となっておらず、タイプコンストラクタ id がついているのがMonad演算では特徴的で、Monad関数などと呼ばれますが、これは後で解説します。 mapFunctor / mapMonad の合成の二項演算子を

'.'

と定義してしておきます。

const flatMapCompose = g => f => a => id(a).flatMap(f).flatMap(g); P(id)['>'](customOperator ('.')(flatMapCompose)); P(f)['>'](customOperator ('.')(flatMapCompose));

id ⋅ f=f=f ⋅ id を検証したいのですが、特別な例外はあるものの、一般に数学で「関数が同じかどうか比較する」ことは不可能で、実際に値をインプットしてみてアウトプットが等しいかどうか調査する、という泥臭い方法でしかないので、ここでは、パイプライン演算をもって、値 4 をleft center rightへインプットし、それぞれのアウトプットを見ています。ここでの問題は、[] が二重にならないか？みたいなことでしかないので、それで十分検証できると見なせるでしょう。

const center = P(4)['>'] ( //center f f );const left = P(4)['>'] ( //e * f = f (id)['.'](f) );const right = P(4)['>'] ( //f * e = f (f)['.'](id) );

log(center); // [8]log(left); // [8]log(right); // [8]

[ 8 ][ 8 ][ 8 ]

Monadはタイプコンストラクタ関数が、左右の単位元となるような二項演算です。 20.9. Monadをもっと厳密にTypeScriptで定義していくここでは、mapFunctorをflatMapMonadにしていきますが、前提として、mapFunctorの構造をしっかりと認識しておく必要があります。

Functorをもっと厳密にTypeScriptで定義していく TypeScriptにおいてはタイプコンストラクタにも当然きちんと型（Type）がつくのですが、ジェネリックを使って、以下のようにタイプ定義します。 type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; 素の値であるAから、タイプコンストラクタであるFによって　F<A>という新しい型（Type）が生み出された、とうまく表現されています。 これは直感的にもわかりやすく美しい表現ですし、配列に限らず他の全ての型にも一貫して応用できるので、A[]やB[]と書く代わりにF<A>F<B>と書いてしまって、 type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0])); const f = (a: number) => a * 2; const A = F(1); // [1] type constructconst B = P(A)['>'](map(f));// [2] mapped このコードでは概念をかんたんに示す目的のために「1要素だけの配列のmap」を定義しています。 型定義だけを改めて抜粋すると、 type F<A> = A[]; // type constructor type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; このTypeScriptのコードで、かなり正確に、Functorの概念を表現できています。 ちなみに、Haskellでは、型定義にプレースホルダは積み増さない流儀なので、 fmap :: (a -> b) -> f a -> f b とFunctorはよりスッキリと定義されてるのですが、全く同じ意味です。 TypeScriptではプレースホルダは逐一明示したほうが便利だ、という方針で、そのメリットは確かに大きいですが、こういう抽象度が高い概念になると、逆に見通しが悪くなるデメリットはありますね。 視覚的に表現するとこういう概念図になるでしょう。 mapFunctorfmap(f)FunctionFunctionmorphismmorphism

MonoidもFunctorもMonadも、人間の工学的な要請とは関係なくアプリオリに存在している代数構造であって、そこが、あとあと設計上の不具合が露呈しがちな、命令型の文（Statement）オブジェクト指向のクラスのあり方と本質的に異なります。 Monadも別に設計するわけではなくて、Haskellのプログラマが「これは使える」と発見した代数構造です。究極的には、こういう代数構造になっているという、形式的な説明しかできません。 mapFunctor

type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>;

flatMapMonadがどう違うのか？というと、対称性です。別の言葉でいうと複数の要素の型（Type）が「等しい」統一された構造になっています。 たとえば、

3 > f >g = 3 > (a → a >f > g)というのと同じように、mapFunctorであっても、もし、 [3] ≫ f ≫ g = [3] ≫ (a → [a] ≫f ≫ g) と二項演算子　≫で、統一されるのであれば、それはmapFunctorでも、identityFunctorの関数合成と同じように、mapFunctorの合成ができるようになる、Monadになる、ということです。 あと、細かいことで混乱しやすいのですが、 (a → [a] ≫f ≫ g)というように、二項演算の頭に、タイプコンストラクタである[a]が必要です。identityFunctorであるパイプライン演算では必要なかったのですが、 (a → a >f > g) (a → identity(a) >f > g)と、二項演算の頭に、identityFunctorのタイプコンストラクタであるidentity関数が暗黙に存在している、と考えれば、整合性がつきます。 そしてまさにこの差の複雑性の増加により、identityFunctor以外のFunctorでは自然と単一の演算子で合成ができずMonadになっていない、と考えられます。

というように、 a → identity(a) >f > g a → [a] ≫f ≫ g とインプット　素の値アウトプット　タイプコンストラクタを通過した上でのFunctor値と、いうタイプをFunctorに昇格させるような関数が自然と出てくることを確認しました。 タイプコンストラクタ関数は原理的に最初からFunctor型に昇格させる型構造になっていて

<A>(a: A) => F<A>

それに加えて、これまで

type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>;

で、

f: (a: A) => B

としていたものを、

f: (a: A) => F<B>　

Functor型に昇格させる型構造であるモナド関数（Monad function）に統一してみれば、

type flatMap = <A, B> // function => function (f: (a: A) => F<B>) => (Fa: F<A>) => F<B>;

となります。念の為に、mapFunctorと比較してみてください。

type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>;

つまり、型構造的には、FunctorとMonadの違いは、

f: (a: A) => B

としていたものを、

f: (a: A) => F<B>　

Functor型に昇格させる型構造であるモナド関数（Monad function）に変えることにしたという、ただ1点のみです。逆に言うと、ここを1個変えるだけで、他のタイプコンストラクタなどとMonad関数的に型が一致して統一されます。つまりFunctorというかMonadを合成したいときに、 (a → [a] ≫f ≫ g)という型構造のものが普通に入ってきても、それは仕様通りなので問題がなくなります。 もちろんこれは、繰り返しになりますが、最初からそうなっているMonadという代数構造を後付け解釈しただけのことですが、こう考えていくと、IdentityFunctorでは、タイプコンストラクタが、Identity関数なので、いちいち書かなくても良くて、

f: (a: A) => F<B>　

は、

f: (a: A) => B

と同じものなので、自動的に諸々は統一されていて、Monadの構造になっている、と解釈することができます。

identityFunctorであるパイプライン演算では必要なかったのですが、 (a → a >f > g) (a → identity(a) >f > g)と、二項演算の頭に、identityFunctorのタイプコンストラクタであるidentity関数が暗黙に存在している、と考えれば、整合性がつきます。

以上が一番外側のアウトラインの説明で、flatMapMonadに限らずすべてのMonadに共通の構造です。 20.10. Monadの実装にはflatという概念が使われているflatMapMonadの実際の実装は、

const flatMap: flatMap = <A, B> (f: (a: A) => F<B>) => (Fa: F<A>): F<B> => Fa.map(f).flat() as F<B>;

Fa.map(f) の値を、flat() している、と結構単純なものになっています。

const f = (a: number) => [a * 2]; // Monad function const A = F(1); 　// [1] type constructconst B = A.flatMap(f); // [2] flatMapped

type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; type flatMap = <A, B> // function => function (f: (a: A) => F<B>) => (Fa: F<A>) => F<B>; const flatMap: flatMap = <A, B> (f: (a: A) => F<B>) => (Fa: F<A>): F<B> => Fa.map(f).flat() as F<B>; { const f = (a: number) => [a * 2]; const A = P(F(1)); const B = A['>'](flatMap(f)); log(B); // [2]}

Array.prototype.flat()は、Array.prototype.flatMap() とセットで同時にES2019で導入されたArrayのメソッドで、最初からflatMapというMonad構造を念頭に実装されています。

flatMap() メソッドは、最初にマッピング関数を使用してそれぞれの要素をマップした後、結果を新しい配列内にフラット化します。これは、map() の後に深さ 1 の flat() を行うのと同じですが、これら 2 つのメソッドを別々にコールするよりもわずかに効率的です。

Array.flatMapのタイプコンストラクタは

const F = // type constructor a => [a];

こういう[]を積み増す方向の関数であり、逆にArray.flat()は、1階層分の構造を潰す（平坦化する）方向の関数です。Array.prototype.flat()からサンプルコードをそのまま引用すると、

const arr1 = [0, 1, 2, [3, 4]];console.log(arr1.flat());// expected output: [0, 1, 2, 3, 4] const arr2 = [0, 1, 2, [[[3, 4]]]];console.log(arr2.flat(2));// expected output: [0, 1, 2, [3, 4]]

どういうMonadであっても、そのタイプコンストラクタで構築される構造があり、そのMonad演算の演算子の関数では、必ずその逆方向に平坦化する操作が行われます。 タイプコンストラクタは、unitと呼ばれることも多く、flatと合わせて語呂も良いので合わせて図式化してみると、

• unit(タイプコンストラクタ) は１階層だけ上げる。　• flat はネストしていれば１階層だけ下げる。 という構造になっていて、どんなMonadのflatに該当する操作でも、せっかく構築した型（Type）を破壊して、素の値がでてくるまでflatしてしまうことはありません。

[[7]].flat() // [7][7].flat() // [7]

このように、Array.flat は、もし Array がネストしてたら、１階層下げて Array を返しますが、ネストしていなかったらそのままの Array を返します。最後の配列の皮を剥いで、裸の値 7 を返すようなことはありません。つまり、Array.flat の返り値は必ず Array タイプである、という基底が保証されている安全な関数です。 20.11. MonadはFunctorのより安全な上位互換となる代数構造 実際にこの安全装置つきのようなflatの実装のおかげで、flatMapMonadはmapFunctorと全く同じように使える上位互換のような代数構造になっています。 Monad関数

const f = (a: number) => [a * 2];

を使う前提であったのがftatMapMonadなのですが、mapFunctorに使うような、Monad関数ではない、これまでどおりの普通の関数

const f1 = (a: number) => a * 2;

を使っても、flatの基底で壊れることなくスムーズに機能します。 ただし、この場合、型定義にひと工夫が必要で、

f: (a: A) => B

と

f: (a: A) => F<B>　

との両方の関数がflatMap関数へのインプットとなるので、

f: (a: A) => B | F<B>

としておく必要はあります。こうしておかないとタイプエラーが出ます。 まとめると、

type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; type flatMap = <A, B> // function => function (f: (a: A) => B | F<B>) => (Fa: F<A>) => F<B>; const flatMap: flatMap = <A, B> (f: (a: A) => B | F<B>) => (Fa: F<A>): F<B> => Fa.map(f).flat() as F<B>; { const f = (a: number) => [a * 2]; const f1 = (a: number) => a * 2; const A = P(F(1)); const B = A['>'](flatMap(f)); const B1 = A['>'](flatMap(f1)); log(B); // [2] log(B1); // [2]}

念の為ですが、これはflatMapMonadの構造の説明のために、車輪の再発明的に自前で実装しただけで、実際はArray.prototype.flatMap() として、最初からメソッドが提供されているので、このように自前実装するまでもなく、使うことができます。

実際にリアル世界のコードで、このように、mapメソッドチェーンを使い倒していて、ある式を、再利用可能な関数として切り出して、別のmapメソッドチェーンに組み入れる、関数の切り貼りのシナリオは普通にありえます。 そこで「関数なので自動的に連結（関数合成）してくれるのだろう」と安心していたら、なんか[[]] と二重の入れ子構造になったデータが出てきた!!原因は不明だ？？というバグが発生しかねません、ということはタイムスパンはわからないですがそのうち必ず発生するでしょう。原因不明の安全でない代数構造を放置して、それに気がつかないままコーディングをしているのだから。 これは、解決すべき重要な問題です。Array.map()はモナド（Monad）ではありません。　この問題はある一定以上のレベルの関数型プログラマの間では認識されていて、その結果、ES2019で新たに実装された、Array.flatMap() メソッドが、モナド（Monad）です。https://github.com/tc39/proposal-flatMap/issues/10 This proposal essentially gives native Arrays the methods they need to work as Monads (without having to extend the prototype). これで [3].map(a => [a].map(f).map(g))　// [[3]] と同じ実験をしてみると、 [3].flatMap(a => [a].flatMap(f).flatMap(g))　// [3] [3] ≫ f ≫ g = [3] ≫ (a → [a] ≫f ≫ g)が想定通り、成立しました。identityFunctorが、identityMonadであったように、flatMapFunctorは同時に、flatMapMonadである、といえます。 (f ⋅ g) ⋅ h=f ⋅ (g ⋅ h)id ⋅ f=f=f ⋅ id

すでに

[3].flatMap(a => [a].flatMap(f).flatMap(g))　// [3]

というのは、JavaScriptのArrayに組み込み済みのArray.flatmapを利用していると同時に、この f も g もMonad関数を説明する前に、map()で使っていた同じf g をまったく問題なく使っていました。 そして、その直後に、

念の為に左右の単位元についても検証しておきます。 id ⋅ f=f=f ⋅ idmapFunctor / mapMonad のタイプコンスタクタid = a => [a] const id = a => [a]; とし、関数 f const f = a => id(a * 2); とのFunctorの合成の二項演算を試行します。　ここで、関数 f が、 const f = a => a * 2; となっておらず、タイプコンストラクタ id がついているのがMonad演算では特徴的で、Monad関数などと呼ばれますが、これは後で解説します。

となったのですが、この左右の単位元の証明のようなときは、さすがに f がMonad関数でないと等式が成立しないので、Monad関数を使っています。 逆に言うと、そういう特別なケースではない大半の利用では、別にそれがMonadであると意識せずとも、Functorの上位互換として使えるので安全性のメリットしかないと思います。これがおそらくHaskell界隈を中心としてなんでもMonad化されている理由のひとつでしょう。 20.12. Monadのつくりかた 概念としてはFunctorのほうがよほど重要で、安全性の要素を考慮しなければ、わざわざMonadを取り扱わなくても、たいていはFunctorだけでも事足ります。まずは自力で必要なFunctorを自由自在に実装できるようになることが先決です。 安全装置つきのようなflatの実装は、今回たまたまflatMapというMonadとセットでES2019で導入されていましたが、一般的には、1. Functorを構築して、それから2. flat的な構造を取り入れてMonadにしていく という流れで、flat的な構造は、タイプコンストラクタで構築した方向と逆の操作を、そのタイプの基底を壊さない安全装置つきで実装する、と自前で実装する必要があります。 そして、新しいFunctorの構成の実例は、後半のReactiveFunctorで紹介しています。 21. 「非同期（Asynchronous）」と命令型プログラミングという技術的負債とasync/await21.1. ノイマン型コンピュータ

ノイマン型コンピュータ

ノイマン型コンピュータとは（ノイマンガタコンピュータ,von Neuman type computer,）ノイマン型コンピュータとは、ハンガリー出身の数学者であるジョン・フォン・ノイマン（John von Neumann）によって提唱された、コンピュータの基本構成（アーキテクチャ）のことである。ノイマン型コンピュータでは、記憶部に計算手続きのプログラムが内蔵され、逐次処理方式で処理が行われる。 中央演算部、制御部、記憶機構、入力部、出力部の5つの部分からなり、プログラム実行時には、主記憶装置から演算制御装置へ命令やデータが記憶レジスタを経由して転送され、命令は、命令アドレスレジスタにセットされたアドレスに沿って逐次的に実行される。 今日の一般的なコンピュータシステムのほとんどが、このノイマン型である。

根本的に、我々が利用して恩恵を受けている現代のコンピュータとはノイマン型であり、ハードウェアの設計として順次処理がデフォルトです。こういうコンピュータというハードウェアに命令を送るプログラムとしてアセンブラ、C、と徐々に抽象化、構造化がなされてきたのですが、このマシンが特定の動作を行うように命令を送る、時系列に命令文を並べたものがコードであり、そのコードを上手に書くことこそがプログラミングである、という歴史的に確立した作法があります。 そして本稿の冒頭で示したとおり、この作法、流儀は延々と現代まで現在進行系で継承されており、非常に不幸なことには、ある程度のプログラミング経験がある中級者以降になっても、おおよそ「これまでこうやってなんとかうまくやってきたのだから」というメンタルブロックが強烈で、なかなか当たり前として刷り込まれた作法を更新することは難しいのが現状です。 ノイマン型コンピューティングで、命令を時系列で順次送り出し、コードはその時系列の順番どおりに物理的に上から下に並べたものである、というある種の常識的なイメージが強固だからでしょう。 その他には、歴史的にコンピュータのハードウェアの性能が限定的で、泥臭い命令型の順次実行ではない、より抽象的なアプローチがパフォーマンスの点で不利になっていたからだと考えられます。さらに、プログラミングではない数学であっても、順次、上から下に計算していく、というのは人間の限られた頭脳ではこちらの作法の方が負担が小さく当たり前に快適だということも考えられます。 グラフ構造が成立していることを考え、依存関係を解決していくようなアプローチは人間の頭脳では現実的ではないので、計算というのは上から下に順次処理していくのが人間にとってもわかりやすい、マシンのパフォーマンスにとってもシンプルで有利だ、とそのような事情が長らくあったのだろうと思います。 21.2. 現代ではノイマン型の命令型思考は技術的負債となっている技術的負債

技術的負債（英: Technical debt）、または設計負債[1]、コード負債とは、ソフトウェア開発における概念であり、時間がかかるより良いアプローチを使用する代わりに、今すぐ簡単な（限定的な）解決策を選択することで生じる追加の手直しの暗黙のコストを反映したものである[2]。 金銭的な負債と同様[3]に、技術的負債も返済されなければ、「利子」が蓄積され、変更の実施が困難になる。技術的負債を処理しないと、ソフトウェアのエントロピーが増大する。金銭的負債と同様に、技術的負債も必ずしも悪いものではなく、プロジェクトを前進させるために（概念実証として）必要な場合もある。一方で、「技術的負債」というメタファーは、その影響を最小限に抑える傾向があり、その結果、修正するために必要な作業の優先順位付けが不十分になると主張する専門家もいる[4] [5]。 コードベース上で変更が開始されると、コードベースの他の部分やドキュメントにも、他の調整された変更が必要になることがよくある。完了していない必要な変更は負債とみなされ、支払われるまでは利息が上乗せされて発生するため、プロジェクトの構築が煩雑になる。この言葉は主にソフトウェア開発で使われるが、他の職業にも適用できる。

ノイマン型の命令型プログラミングというアプローチはまさに技術的負債という概念に合致します。原因としていろいろ列挙されているのですが、思い当たる事が多いです。

原因技術的負債の一般的な原因は次のとおり。 • 継続的な開発：時間をかけてプロジェクトを強化していくと、古いソリューションは最適ではなくなる。• 不十分な先行定義：開発中に要件がまだ定義されていない場合、設計が行われる前に開発が開始される。これは時間を節約するために行われるが、後になって手直しをしなければならないことがよくある。• ビジネス上のプレッシャー：必要な変更が完了する前に、ビジネスが何かをすぐにリリースすることを検討する場合、未完了の変更からなる技術的負債が蓄積される[6] [7]。• プロセスや理解の欠如。企業が技術的負債の概念に気付かず、その影響を考慮せずに意思決定を行う。• 緊密に結合されたコンポーネント。機能がモジュール化されていないため、ソフトウェアはビジネスニーズの変化に対応できるだけの柔軟性を持たない。• 知識の欠如：開発者がエレガントなコードの書き方を知らない場合[7]。• オーナーシップの欠如：ソフトウェアの外注化により、社内のエンジニアリングが外注コードのリファクタリングやリライトを要求される場合。

古いソリューションは最適ではなくなるという指摘ですが、たしかにノイマン型のハードウェアの限られたリソースや、あるいはアセンブラや、より抽象化が進んだ高級言語であってもせいぜいC言語しかない、という時代においては、命令型のアプローチは最適でありつづけました。 そしてハードウェアがこういう単一のフレームワークの中では最適であったアプローチが、現代では、CPU自体がマルチコア化も進み、また最近特に著しいクラウド化が進み、ハードウェアと言う代物自体が単一の存在、命令を送る物理的デバイス、という意味が消滅しつつあります。 分散コンピューティング

分散コンピューティング（ぶんさんコンピューティング、英: distributed computing）とは、プログラムの個々の部分が同時並行的に複数のコンピュータ上で実行され、各々がネットワークを介して互いに通信を行いながら全体として処理が進行する計算手法のことである。複雑な計算などをネットワークを介して複数のコンピュータを利用して行うことで、一台のコンピュータで計算するよりスループットを上げようとする取り組み、またはそれを実現する為の仕組みである。分散処理（ぶんさんしょり）ともいう。並列コンピューティングの一形態に分類されるが、一般に並列コンピューティングと言えば、同時並行に実行する主体は同じコンピュータシステム内のCPU群である。

並列計算

並列計算（へいれつけいさん、英語: parallel computing）は、コンピュータにおいて特定の処理をいくつかの独立した小さな処理に細分化し、複数の処理装置（プロセッサ）上でそれぞれの処理を同時に実行させることである[1]。並列コンピューティングや並列処理とも呼ばれる。大きな問題を解いたり、大量のデータを処理したりする過程は、より小さなサブタスクやサブデータグループの処理に分割できることが多い、という事実を利用して単位時間あたりの処理効率（スループット）の向上を図る手法である。

可能性と問題点並列計算は、プロセッサ同士が独立して同時に仕事をするため、理想的な状況下ではプロセッサの回路規模を大きくすること無く、プロセッサの数に比例して処理性能が向上できると考えられ、スーパーコンピュータなどで古くから採られた手法である。スーパーコンピュータの高い性能は、プロセッサ数やノード数がパーソナルコンピュータに比べて極めて多く、並列処理性能が高いことも重要な要因である[2]。 しかし、問題点もある。並列計算を行う場合、もっともパフォーマンスを発揮するのはこれら複数のプロセッサが全て100%使い切られた時と考えられるが、従来のプログラムの多くは、複数のプロセッサを均等に全て使い切るようにはできておらず、また、そういったプログラミングは難しい。

背景従来、コンピュータソフトウェアは逐次的に計算されるものとして書かれてきた。問題を解くためにアルゴリズムが構築され、それによって逐次的に実行される命令列が生成される。その命令列は、コンピュータのCPU上で実行される。命令は一度に1つずつ実行される[3]。 一方並列計算では、複数の計算ノードが同時並行的に動作して問題を解く。問題は独立した部分に分割され、各計算ノードがアルゴリズムの一部を同時並行的に実行する。計算ノードの実体は様々であり、マルチプロセッサ型のコンピュータの各CPUだったり、ネットワーク上のコンピュータだったり、専用ハードウェアだったり、それらの組合せだったりする[3]。

このように、「従来のハードウェア構成」にとって最適でありつづけた「従来のソフトウェア」というのは、「現代のハードウェア構成」においては、そっくりそのまま技術的負債となってしまいます。つまり、怠惰や惰性によってすでに技術的負債となってしまっているアイデアをデフォルトと位置づけて安心していると、それは全部「解決すべきなのだが、解決がとても難しい問題」となって必ずしっぺ返しを食らうことになります。 「現代のハードウェア構成」というのはAWSやAzureそれからGoolgeClougPlatformのような「計算資源のコモディティ化」です。クラウドという抽象的なハードウェアから計算資源を切り出して購入します。この場合、原理的に、「計算ノード」が「ネットワーク上のコンピュータ」である並列計算になっていますから、単一のノイマン型ハードウェアに逐次の命令リストを送る、という命令型アプローチはまるで最適ではないのです。 技術的負債をデフォルトとするメンタルブロックは、新しい状況においては、これまで慣れ親しんで積み重ねてきた自身の技術的手法が全く通用しない、すべて1から学習しなおす必要がある、という精神的不安となって返ってくることになります。 21.3. 「非同期（Asynchronous）」という用語巷には、「非同期（Asynchronous）」という言葉そのものを説明するようなページがとても多いです。 そして多くの場合その説明に欠落しているのが、そもそも、「同期（Synchronous）処理」というものが、ノイマン型コンピューティングの命令型コードによる逐次処理のことである、という知見です。 非同期処理は、そのまま分散コンピューティング、並列処理、クラウドコンピューティングという概念にとっては、現代においてはむしろこちらのほうが最適化されている当然のアプローチとなります。 ここで、厄介なのが、ノイマン型コンピューティングの命令型コードによる逐次処理のことである同期（Synchronous）処理が、多くの技術者のマインドセットとしてデフォルトの素地として存在していて、非同期（Asynchronous）処理が、なにか特別な新しい概念のように取り扱われがちなことです。そして、「解決すべきなのだが、解決がとても難しい問題」として非同期処理は考えられがちです。 これは、技術的負債を放置した結果しっかりとしっぺ返しを食らっている現状を端的にあらわしている証拠のひとつです。 最初は、ノイマン型コンピューティング、命令型を、まあこれまでこれでやってきたことだし、命令型コードというのは最初に当たり前に習うんだかから、と問題としては捉えてはいません。しかし、しばらく経ってから、巡り巡って「非同期（Asynchronous）」って一体何？なんか難しそうな概念ですね！となってしまっているのです。 21.4. JavaScriptの非同期関数（Async function）async/awaitJavaScriptで最近(ES7)導入されて普及しているasync/awaitは、この技術的負債の権化のような存在です。多くのプログラマは技術的負債であるとは気が付かないまま利用して普及しているのが、まさに技術的負債ぽいですね。 まず、JavaScriptには、Promiseという非同期処理のための関数があります。

Promise オブジェクトは、非同期処理の完了 (もしくは失敗) の結果およびその結果の値を表します。

Proimise はちょっと出来の悪いFRPのFunctorです。出来は悪いのですが、Functorという代数構造として実装されていることはかなり良いことです。 そして、なんとこの「代数構造としての良さ」を帳消しにしたい人たちが多くて、わざわざasync

非同期関数は async キーワードで宣言され、その中で await キーワードを使うことができます。 async および await キーワードを使用することで、プロミスベースの非同期の動作を、プロミスチェーンを明示的に構成する必要なく、よりすっきりとした方法で書くことができます。

というのが導入されました。

The async and await keywords enable asynchronous, promise-based behavior to be written in a cleaner style, avoiding the need to explicitly configure promise chains.

プロミスチェーンを明示的に構成する必要なく、よりすっきりとした方法で書くことができます。

Promiseというのは代数構造であるFunctorであり、プロミスチェーンというのは、二項演算の連鎖という式のことですが、「明示的に構成する必要なく」って代数構造を明示する必要がない、ということを平気で主張しています。結構信じられません。信じられないことが普通に起こってしまうのが、まさに技術的負債の世界の恐ろしさなのです。 英語原文においても、 a cleaner style, avoiding the need to explicitly configure promise chains.と書かれていて、これはある種の世界的コンセンサスを得て表示されている、ということを意味します。 代数構造の式を書き下すほうが、明らかに、cleaner styleで、スッキリとした方法なのですが、彼らがいう「スッキリとした方法（cleaner style）」とは、

もちろん、命令型コードにおける構文（Statement）です。

非同期関数には、 await 式を置くことができます。 await 式は返されたプロミスが履行されるか拒否されるまで実行を中断することで、プロミスを返す関数をあたかも同期しているかのように動作させます。

async/awaitを使うと、PromiseFunctorという代数構造の式を書かなくても非同期処理をよりわかりやすく同期処理的に命令型の構文で書けるようになる そう堂々と主張されています。 別の人は、

ts-pattern より良い、より安全な条件（condition）を書きましょう。パターンマッチングを使えば、複雑な複数の条件を、単一のコンパクトな式（expression）で表現できます。コードが短くなり、読みやすくなります。 パターンマッチングとは何ですか？パターンマッチングとは、関数型プログラミング言語に由来する技術で、値の構造に基づいて条件付きコードの分岐を宣言的に記述するものです。この技術は、特に複雑なデータ構造や複数の値で分岐する場合に、命令型の代替物（if/else/switch文）よりもはるかに強力で、はるかに冗長性が少ないことが証明されています。 パターンマッチングは、Haskell、Rust、Swift、Elixir、その他多くの言語で実装されています。EcmaScript仕様にパターンマッチングを追加するためのtc39プロポーザルがありますが、まだステージ1であり、この先数年は実装されそうにありません（仮に実装されることがあったとしても）。幸運なことに、パターンマッチングはユーザーランドで実装することができます。 ts-patternは、タイプセーフなパターンマッチングの実装を提供しており、今日から使い始めることができます。

と主張し、逆にTC39では、

それ以前にTC39プロポーザル版Pattern Matchingは、どのような実装になっているのでしょう？ うーん、なんか文（Statememt）になっていますね・・・元々Pattern Matchingとは関数型プログラミングが発祥であり、式（expression）であるのが普通なのに。ts-patternのコードでは純粋に簡潔に二項演算の式として構築できることとは対照的です。 const sanitize = name => match(name) .with('text', 'span', 'p', () => 'text') .with('btn', 'button', () => 'button') .otherwise(() => name); これは何を意味するのか？というと、ts-patternライブラリの作者はPattern Matchingがなんたるかという本質とそれによってもたらされる効能、より良い、より安全な条件（condition）を書きましょう。パターンマッチングを使えば、複雑な複数の条件を、単一のコンパクトな式（expression）で表現できます。コードが短くなり、読みやすくなります。パターンマッチングとは、関数型プログラミング言語に由来する技術で、値の構造に基づいて条件付きコードの分岐を宣言的に記述するものです。この技術は、特に複雑なデータ構造や複数の値で分岐する場合に、命令型の代替物（if/else/switch文）よりもはるかに強力で、はるかに冗長性が少ないことが証明されています。を良く理解していてその強い理念と情熱をもって実装しているのに対して、本件のTS39プロポーザルの参加者は、需要がありそうだしやってみよう、標準化されたら自分の功績にもなるし、という功名心（全員がそうではないが筆者が直接やりとりしたこともあるアカウントの参加者（あまりレベルが高いプログラマとは見做せない）を見てたらおそらくそんなところ）で、さらに背景には「JavaScriptはあくまで命令型の文の集まりとして記述されるべきだ」という信念のようなものが共有されており、switch/case文との後方互換性を維持したかったのだろうと想像します。

TC39では、基本的に命令型の構文を導入することに懸命で、というかおそらく内部にそういう強い思想と主張をもった人間が存在するのでしょうが、教条化しているようです。 async/awaitというのは、1. PromiseFunctorという代数構造の式や「プロミスチェーン」と呼ばれる二項演算の連鎖の式（Expression）は明示したくない2. より「スッキリとした方法（cleaner style）」つまり命令型の文（Statement）の方が良いという、よくわからない信念、教条をもつひとたちのためのものですから、この信念に同意できない場合は、みんなが使っているから、自分のプロジェクト範囲に与えられているから、という同調圧力にならう以外の利用する合理性、メリットは一切ないです。 そして、こういう無意味な構文の発明というのは、たいてい不整合さを無用に発生させます。 実際にそのページには、

と、Functorや二項演算の連鎖を、わざわざ命令文の列挙に加工したことから発生する、新しいルールが付与されています。 新しいルールにプログラマが注意を従わない可能性が十分に想定されるからこそ、Note:これを知っている必要があります、さもなければエラーが発生しますよ！わざわざ「親切」に記載しておく必要があるのですね。 ということはプログラマが全力で回避すべき「複雑性」を追加していることになりますが、あんまりそういうことは気にしないスタイルなのでしょう。基本的に、ちょっとくらい新しいルールが追加されても、プログラマがそれに注意を払えばかんたんに解決するはなしだ、大した問題にはならないはずだ、という愚かな楽観論に基づいています。 基本的に命令型の構文を正当化をするときには、議論は全部こんな感じになります。 また、

「両者は同等ではありません。」「異なる参照を返します。」 非常に恐ろしい事実が宣言されています。つまり、「ソフトウェアの複雑性」は組み合わせ爆発が根本要因であり、「等しい」という価値を重視すれば、原理的に組み合わせ爆発のリスクを回避できる、という原理原則に反するものです。 その結果「問題になることがあります」と「仕方がないですよね」的に書かれているのですが、そもそも、代数構造の式（Expression）を命令型の文（Statement）として書き下すほうが「スッキリとした方法（cleaner style）」だという強い信念により好んでわざわざ後付けしたわけなので、別に「仕方がない」ことはありません。最初から余計なことはしなければ、組み合わせ爆発の唯一要因である「等しくない」「区別すべき要素」は発生していないのです。 技術的負債の世界は恐ろしいですよね。非常に愚かなアプローチです。 なんでこんなことになるのだろう？とは思いますが、結局のところ、こういう不合理な信念、教条というものは、「精神的な弱み」に起因するのであって、

この場合、原理的に、「計算ノード」が「ネットワーク上のコンピュータ」である並列計算になっていますから、単一のノイマン型ハードウェアに逐次の命令リストを送る、という命令型アプローチはまるで最適ではないのです。 技術的負債をデフォルトとするメンタルブロックは、新しい状況においては、これまで慣れ親しんで積み重ねてきた自身の技術的手法が全く通用しない、すべて1から学習しなおす必要がある、という精神的不安となって返ってくることになります。

というようなことだと想像します。 Promiseは、実装は複雑でけして出来の良いFRPではありませんが、ひとつのFuncorであり代数構造なので二項演算の連鎖なりを書けば良いのですが、命令型ではありません。これまでと勝手が違うことは感じられます、そこであえて慣れ親しんでいる命令型の構文の列挙という既存のスタイルに固執するほうが「スッキリとした方法（cleaner style）」と感じられる、精神的な安定が得られる、そうとしか説明のしようがありません。 22. 関数型リアクティブプログラミング（FRP） 時間に依存する関数型コードの書き方 22.1. 命令型コードは時間とコードの配置場所に暗黙に依存しているこの章のメインテーマは「時間」です。 プログラミングは数学的な作業であり、工学的な作業ですから、当然、理系分野とみなされるのですが、同じ物理学ではニュートン物理学あるいはそれ以前から、かなり客観視されて研究されてきた時間という概念を、かなり巧妙に回避しながらプログラミングの体系を構築し議論しようとしています。 命令型コードははあくまでコードの構造の主体がフロー文であり、依存グラフ（Dependency graph）など最初からまったく考慮していない各種変数の値がバラバラに各自それぞれ独自のルールにもとづいて刻々と変化していくので、途中のパーツを交換してみたら、なにか時系列の観点で不整合がかんたんに発生してしまい、プログラマにとっては想定不可能だった不具合が生じます。 これは多くの（命令型）プログラマーが普段の経験として痛感している事実でしょうし、DEBUGのために生産性が致命的に損なわれています。 関数型コードは依存グラフで構成された式である他方で、命令型コードは時系列に依存しているのです。 22.2. 命令型コードで普通にやっている値の書き換えというのは一体なんなのか？ ミュータブル（mutable）な世界

命令型コードははあくまでコードの構造の主体がフロー文であり、依存グラフ（Dependency graph）など最初からまったく考慮していない各種変数の値がバラバラに各自それぞれ独自のルールにもとづいて刻々と変化していく

という命令型の作法は普通に行われていますが、そもそも、値の書き換えってなんでしょうか？ プログラミングとは根本的には数学的作業なのですが、ここにある値、A = 1というのがあるとします。この値を書き換える、っていうのは、A = 2などにするということですよね？ 数学的には破綻しています。義務教育を受けていれば誰でもすぐにわかることです。もしくは、「いやプログラミング特有の代入なんで、数学的には破綻していない！」というのであれば、「数学とは違うプログラミング特有のまた別のなにかの概念」を暗黙に導入しながら数学的ではない方法を採用している、ということなので、いずれにせよ純粋に数学的なプログラミングはやってない、ということになります。 背景にはもちろん、ノイマン型コンピュータへの命令を送っているだけであって逐次処理にすぎないなのだから、という理屈があります。命令型プログラミングに入門すると、まずこういうふうにやれ、と教わるのです。 ノイマン型コンピューティングである命令型の逐次処理という歴史的背景による実践があるにしても、数学的に破綻しているのは、数学的な作業であるプログラミングではかなりマズいです。したがって、値を書き換える真似は避けよう、と考えれば、「値の不変性」英語で言えばイミュータブル（Immutable）にする、という方針になります。　

イミュータブル (英: immutable) なオブジェクトとは、作成後にその状態を変えることのできないオブジェクトのことである。対義語はミュータブル (英: mutable) なオブジェクトで、作成後も状態を変えることができる。

さて、ここで重大な問題が発生してしまいます。我々が暮らしている「現実世界」はミュータブル（mutable）なのです。 現実世界というのは刻一刻と変化していきます。数学的整合性のあるimmutableで一貫したプログラミングをしていく、そんな方針などは机上の空論で、だから関数型プログラミングという理想論は現実的なアプリケーションを開発するのには使いものにはならない、と考えることができます。 実際にそういう認識が大勢であった時代は長く続いていました。 整理すると、 • 数学世界 immutable• 現実世界 mutable• このようなマインドセットがまずあるわけです。両者は一致しない、じゃあどうしよう？ 原始的な命令型パラダイム、あるいはオブジェクト指向の大半の作法では、我々の素朴な直感のマインドセットに忠実に従って、数学世界のほうを捻じ曲げることにします。 • 数学世界（エセ）mutable• 現実世界 mutable とします。これで現実世界とエセ数学世界の一致となりました。 エセ数学世界、っていうのは A = 1A = 2 みたいな並びを普通に許容します。普通の命令型のコードです。

var A;A = 1;A = 2;

値の変更を許すことはないimmutableの世界ではないほうの、mutableな世界です。 コードの並び方に依存して論理が決まっていく世界です。つまり、数学ではなくコードの並び方のほうが重要なのです。 この、エセ数学世界での各種操作が旧来の意味での原始的なプログラミングの作法である、と言えるでしょう。当然のように発生している眼の前の数学的不整合についてはその都度ごまかしごまかしやっていくわけです。 22.3. イミュータブル（Immutable）な世界 根本的に何かが間違っている。何か見落としている。それは「時間」の概念です。 きちんと時間の概念を導入してやれば、時間t1t2でA(t1) = 1A(t2) = 2とできて、数学的に破綻しなくなります。たったそれだけのことです。 これだとコードの並びに依存しません、入れ替わったって別に大丈夫です。純粋に数学的だと言えます。 そしてもっと話を広げると、これは我々の現実世界でも同じです。宇宙の時空構造を記述する物理学は数学で記述されています。 時空構造には時間軸があり「時間」は物理学の理論を構築している数式のパラメータのひとつでしかありません。 これは特に、理論物理学の素養があれば、ごく普通の知見であり世界観でしょう。

A Stubbornly Persistent Illusion: The Essential Scientific Works of Albert Einstein | スティーブン・ホーキング

The distinction between the past, present and future is only a stubbornly persistent illusion.過去、現在、未来の区別というのは、頑固につきまとう幻想に過ぎない — アルバート・アインシュタイン

In which ways can we visualise the space-time continuum?時空連続体はどうやって可視化できるのでしょうか？

アインシュタインは、彼のとっての宇宙を、何も動かず（！）、起こりうることはすべてすでに起こっており（！）、過去も未来も（！）起こり続けている「固いブロック」（ブロック宇宙）として思い描いていました。アインシュタインにとっての時間は、このブロックの仮想的な「スライス」でした。 すべての時間が現在みたいなもの

ということで、わざと嘘を書いてしまった前言

さて、ここで重大な問題が発生してしまいます。我々が暮らしている「現実世界」はミュータブル（mutable）なのです。

を撤回させていただいて、現実世界も数学・物理学的な俯瞰では、immutableです。 従って、• 数学世界 immutable• 現実世界 mutableと素朴に考えるマインドセットが間違っていたのです。 また、その素朴に間違っているマインドセットのつじつま合わせをするために、数学世界のほうを捻じ曲げる• 数学世界（エセ）mutable• 現実世界 mutableというアプローチも間違っています。 正しくは、• 数学世界 immutable• 現実世界 immutableとなっているのでなんの問題もありません。 22.4. GitはImmutableな永続データ構造（Persistent data structure） • 数学世界 immutable• 現実世界 immutable• 実際にこういうモデルはプログラミングの世界ではよく使われています。 バージョン管理システム で、Gitがメジャーです。

Gitでは

このように時間軸でバージョンが更新されるレポジトリをImmutableなデータ構造で管理しています。 GitHubでは、このようにHistoryがありますが、Immutableなデータ構造になっています。

このようなデータ構造を永続データ構造（Persistent data structure）といいます。

永続データ構造（えいぞくデータこうぞう、英: Persistent data structure）は、変更される際に変更前のバージョンを常に保持するデータ構造である。このようなデータ構造は、更新の際に元のデータ構造を書き換えるのではなく、新たなデータ構造を生成すると考えられ、イミュータブルなデータ構造の構築に利用可能である。

22.5. 関数そして二項演算子は暗黙に時間依存してはならない 副作用がない純粋な関数（Pure function）状態を持たない純粋な関数 というのが、より一般的な言い方ですが、いろいろ解説を読んでも、最終的には要するに.、「時間依存しない」という事実を、「時間」というキーワードを避けながら説明されています。「時間依存しない」というのは、つまりImmutableである、いうことです。 純粋、副作用、それから参照透過性というバズワードの問題点は、たとえばこのコードは純粋と言えるのか？これは副作用と言えるのか？と、時間依存の扱いという本質とははずれたところで言葉の定義議論という本末転倒で不毛な議論に必ず陥るからです。 いわゆる「純粋な関数」とは、厳密にその関数の引数のみに依存していると一応の説明はされます。 関数型コードの式を組み立てていくときは、関数そして二項演算子と（）を活用して依存グラフを構成します。 では、この関数はどうか？

const x = 5;const f = a => a + x;

「純粋な関数」とは、厳密にその関数の引数のみに依存していると考えたとき、この f 関数は関数の引数であるaのみに依存しておらず外部変数であるxにも依存しているだろう？という疑念が出てきて当然です。 しかし、このxは「定数」で、時間変化せず、常に5と等しく、安全に置き換え可能なので、時間依存していません。Immutableです。 関数の別の表記である二項演算子、二項演算についても同様です。演算は左右の被演算子（Operator）2つのみに依存して、依存グラフを構成しなければいけません。 幸いなことに、二項演算の場合は、命令型プログラミングでは当たり前のようにやっている時間依存する演算みたいなことは当たり前ではなく、小学校の算数の教育からずっと、「計算」したらそれで値が決まる、という意識は強く、計算する時間によって答えがコロコロと変わる、というのはむしろ珍しい現象におもえることでしょう。 つまり、我々は義務教育の頃には、演算というものは時間依存しないものである、という正しい作法を徹底的に叩き込まれており、その次に、命令型プログラミングなるもので、コードに出てくる関数では、演算する時間、タイミングによって、値がコロコロと変化する、時間依存するのが当たり前である、という間違った作法を再教育されているわけです。今一度小学校の算数の頃の意識に戻り、演算というものは時間依存しないものである、と頭をリセットしなおす必要があります。 コードの論理的な依存グラフより外の外部と接続しているIOが副作用があり純粋ではない、と言われる理由は、コードの外の現実世界の「時間」に依存しているからです。現実世界は壮大な時間依存するグラフです。 そして現実世界はImmutableな宇宙なので、別に依存してもかまわないですし、ユーザからの入力やコンソールへの出力をはじめIOでは実際に依存する必要があります。 しかしそのときは、暗黙にやってはいけません。 22.6. 関数そして二項演算子が時間依存するときは明示的に依存グラフを構成する

計算可能な有向非巡回グラフ（DAG） 巡回グラフあるいは、有向閉路グラフ (directed cycle graph)になっていない、つまり、計算可能で無限ループになってないグラフのことは、有向非巡回グラフ（Directed acyclic graph）と呼びます。 有向非巡回グラフ、有向非循環グラフ、有向無閉路グラフ（ゆうこうひじゅんかいグラフ、英: Directed acyclic graph, DAG）とは、グラフ理論における閉路のない有向グラフのことである。有向グラフは頂点と有向辺（方向を示す矢印付きの辺）からなり、辺は頂点同士をつなぐが、ある頂点vから出発し、辺をたどり、頂点vに戻ってこないのが有向非巡回グラフである[1][2][3]。 有向非巡回グラフは様々な情報をモデル化するのに使われる。有向非巡回グラフにおける到達可能性は半順序を構成し、全ての有限半順序は到達可能性を利用し有向非巡回グラフで表現可能である。順序づけする必要があるタスクの集合は、あるタスクが他のタスクよりも前に行う必要があるという制約により、頂点をタスク、辺を制約条件で表現すると有向非巡回グラフで表現できる。トポロジカルソートを使うと、妥当な順序を手に入れることができる。加えて、有向非巡回グラフは一部が重なるシーケンスの集合を表現する際の空間効率の良い表現として利用できる。また、有向非巡回グラフはイベント間の因果関係を表現することにも使える。さらに、有向非巡回グラフはデータの流れが一定方向のネットワークを表現することにも使える。 有向非巡回グラフ（Directed acyclic graph, DAG）は、依存グラフ（Dependency graph）のなかで依存関係のサイクル（循環依存関係）が存在しない特殊なケースであり、関数型プログラミングあるいは本稿で、依存グラフというときには、有向非巡回グラフ（Directed acyclic graph）のことを意味します。原理的に計算可能なのはこちらでしかないからですね。 In a dependency graph, the cycles of dependencies (also called circular dependencies) lead to a situation in which no valid evaluation order exists, because none of the objects in the cycle may be evaluated first. If a dependency graph does not have any circular dependencies, it forms a directed acyclic graph, and an evaluation order may be found by topological sorting. 依存関係グラフにおいて、依存関係のサイクル（循環依存関係とも呼ばれる）は、サイクル内のどのオブジェクトも最初に評価することができないため、有効な評価順序が存在しないという状況を引き起こす。依存グラフに循環依存性がない場合、それは有向非巡回グラフ（DAG）を形成し、トポロジカルソートによって評価順序を見つけることができる。 有向非巡回グラフはイベント間の因果関係を表現することにも使える。 というのは、関数型プログラミングの文脈でいうと、関数型リアクティブプログラミング（FunctionalReactiveProgramming）つまりFRPのことです。 演算可能な式を二項演算子やグループ化演算子（）を活用して代数的に構成することは、有向非巡回グラフ（Directed acyclic graph, DAG）を構成することであり、これはそのままイベント間の因果関係を表現することが可能です。

現実世界の時間に依存するコードを書くときは、各イベント間の因果関係を表現する依存グラフ、有向非巡回グラフ（Directed acyclic graph, DAG）を構成します。 これはとっかかりがイベントであるだけで、これまで

関数型のコードでは、二項演算子とともにグループ化演算子 ( ) を組み合わせることで依存グラフを構成し、演算はその依存グラフを解決する形で進んでいく。依存グラフを構成する二項演算を最大限に活用した式の組み立てに注力することで、バグの入り込む余地が極小の関数型コードを書くことが実現できる。

とやってきたこととまったく同一のアプローチです。 各イベント間の因果関係を表現する依存グラフ、有向非巡回グラフ（Directed acyclic graph, DAG）を構成することが、関数型リアクティブプログラミング（FunctionalReactiveProgramming）つまりFRPです。 その式（Expression）を構成しますが、その役割を担う代数構造はFunctorやMonadという二項演算です。 22.7. 時間軸上のイベントを参照する関数タイマーイベントsetTimeout()キッチンタイマーやスマホOSのタイマーと同じで、セットした瞬間から、セットした時間の後でイベントを発生する時間関数です。 これはタイマーをセットした瞬間を0として、時間軸の相対座標でtの時間に依存関係を構築すると見なせます。そういう関数です。 その他ユーザー入力のIOでトリガーされるイベントをはじめ、いろいろあるようです。イベントリファレンス 22.8. イベント駆動型プログラミング（Event-driven programming）イベント駆動型プログラミング

イベント駆動プログラミング（イベントくどうプログラミング、英: event-driven programming）とは、ユーザー側の操作による受動的なイベントの発生によって、コンピュータ側の能動的なプロセスの実行とプログラムフローの選択が決定されるというプログラミングパラダイムである。イベントドリブンとも邦訳される。グラフィカルユーザーインターフェース（GUI）ソフトウェアでよく用いられており、ユーザー入力に対するレスポンス出力の実装に適している。デバイスドライバプログラムでも多用されている。 ここで言うイベントとは、マウスクリックやキーボード押下によるユーザー操作、センサーやシグナル受信によるハードウェア入力、走行スレッドや発生トランザクションからのメッセージ受信を指している。プロセスの実行とは、スレッドの開始や手続き/関数の呼出しを指している。

イベント駆動（event-driven）という概念は、イベントをトリガーにある関数を適用する、というもっとも基本的で素朴な概念です。ただそのことだけ、言い表しており、それ以上のことはなにもありません。 22.9. リアクティブプログラミング（Reactive programming）Reactive programming

In computing, reactive programming is a declarative programming paradigm concerned with data streams and the propagation of change. With this paradigm, it's possible to express static (e.g., arrays) or dynamic (e.g., event emitters) data streams with ease, and also communicate that an inferred dependency within the associated execution model exists, which facilitates the automatic propagation of the changed data flow. コンピュータにおけるリアクティブプログラミングは、データストリームと変化の伝播に関する宣言的なプログラミングパラダイムである。このパラダイムでは、静的なデータストリーム（配列など）や動的なデータストリーム（イベントエミッタなど）を簡単に表現することができ、また、関連する実行モデル内に推測される依存関係が存在することを伝えることで、変更されたデータフローの自動伝搬を容易にすることができる。

リアクティブプログラミング（Reactive programming）では、もう少し高度なことが書かれています。 イベント駆動型プログラミング（Event-driven programming）をベースに抽象化して高度な操作が可能になって枠組みと考えて良いでしょう。 最初の「イベント」はデータの変更というように抽象化されます。 たとえば、HTML/JavaScriptでいうと、

<button label="Click me" onclick="alert('Hi')"/>

これが、イベント駆動プログラミングのコードです。 ユーザによるボタンClickイベントが、alert関数の適用に直接、紐付いています。非常に直接的で単純でわかりやすいですし、一度はこういうコードを書いた人は多いのではないでしょうか？ でも、こういうのはあんまり洗練された設計ではありません。なぜならば、イベントと具体的な関数適用が直結している、結合が密すぎるからです。 たとえば、alert命令だけじゃなくて、他にもいろいろやらせたかったり、このクリックイベントと、また別のイベント、たとえばダブルクリックだったり、ドラッグだったり、そういうのと組み合わせるシナリオは普通に考えられるわけで、そういう場合、このコードはあっさり破綻します。これ以上どうすれば良いのかわからない、複雑性に耐えられない。つまり、よろしくないコードです。 そこで、イベントと具体的な関数適用を直結させるのではなくて、その中間にリアクティブ値というデータを用意します。そうすることで、そのリアクティブ値は、他の関数適用と紐付けることができますし、リアクティブなデータ構造として抽象化されているので、別のリアクティブなデータ構造と組み合わせて複雑なことでも自在に出来るようになります。 これはつまり、リアクティブなデータで依存グラフを構成する、ということです。

あらかじめ設計された依存グラフに従って、データの変更はイベント駆動するのでドミノ倒しのように伝播していきます。

これはまさに、関数型リアクティブプログラミング（FunctionalReactiveProgramming）つまりFRPそのものであるように思えます。 実際に、このあたりの用語、概念は分類の問題でしかなく、境界は曖昧です。たとえば、他にもデータフロープログラミング（Dataflow programming）

データフロープログラミング（英: dataflow programming）は、データフローの原理とアーキテクチャに準拠してプログラムを、オペレーション間のデータフローの有向グラフとして模型化するというプログラミングパラダイムである。データフロー言語は、関数型言語の特徴を共有しており、より数値処理に適したものになっている。

「データフローの有向グラフとして模型化する」さらに「関数型言語」とか書いてあるんだし、だったらそれはFRPなんじゃないの？と思えます。 こういう専門用語は、これに限らず複数あります。 誰々がパイオニアである、と書かれていることも多くて、基本そういう功績のために新しい用語がつくられたり、そういう用語の混乱はよくあることなので、あまり気にする必要もないですし、本末転倒になって不毛なことです。 基本的に、プログラミングを含む工学では、なるだけ既存の数学的な概念と用語を踏襲すべきであって、同じ意味の造語を無闇に増やすことはあまり意味がないどころか、混乱をもたらすだけだと考えます。 22.10. PromiseはJavaScriptに導入された時間軸上のイベントのFunctor古いコールバック API をラップする Promise の作成 PromiseはJavaScriptに導入された時間軸の二項演算

const promise = new Promise( resolve => setTimeout(resolve, 3 * 1000)); const f = () => console.log("3 seconds"); promise.then(f); //returns promise object

極めて限定的ながらPromiseはJavaScriptに導入された時間軸の二項演算で、二項演算子はthenになりますが、Promise.thenが登録されて監視するイベントについては繰り返し参照することはできません。たとえば、このサンプルのように、setTimeoutではうまく機能しますが、setIntervalを利用したタイマーカウンタを実装することは不可能です。局所的に一度トリガーされてしまうとそれで終わりなので、不完全なFRPであるとは言えます。 23. シンプルでミニマルかつ強力なFRPの実装 23.1. DemoReactive programmingのWikipedia項目の前半部分に、FRPのDemoにちょうど良さそうなコードがあるので、それを活用します。コードを引用すると、

var b = 1var c = 2var a = b + cb = 10console.log(a) // 3 (not 12 because "=" is not a reactive assignment operator)

前半は普通の命令型のコードで、一旦、

var a = b + c

と定義というより「代入」したあとで、

b = 10

と、bを「破壊的代入」しても、a の値についてはすでに計算済みなので影響を受けません、という、まずまず命令型プログラマにとっては、常に考える対象となる事柄で、特に工夫のない関数型コードであっても、ある程度共有できるアイデアが説明されています。その後で、長いコメントがあり、

// now imagine you have a special operator "$=" that changes the value of a variable (executes code on the right side of the operator and assigns result to left side variable) not only when explicitly initialized, but also when referenced variables (on the right side of the operator) are changed

ここで、明示的に初期化されたときだけでなく、（演算子の右側で）参照される変数が変更されたときにも、変数の値を変更する（演算子の右側でコードを実行し、その結果を左側の変数に代入する）特殊な演算子「$=」があるとします。

と仮想的なリアクティブ演算子があるという説明があり、その後、その仮想リアクティブ演算子を利用したリアクティブプログラミングのコードがあります。

var b = 1var c = 2var a $= b + cb = 10console.log(a) // 12

まずまずリアクティブというアイデアは理解しやすい、特に命令型コードに慣れ親しんでいるプログラマにとっては、コードの上下のフローが逆行するようなありえないことが実現しているよう見えます。 この仮想的なリアクティブなコードを、今から実装するFRPの実際のコードに書き直します。

const b = IO(1);const c = IO(2); const a = allNoResetIO([b, c]) ['>='](([b, c]) => b + c); b['>'](next(10));const Log = a['>='](log); // 12b['>'](next(100)); // 102

12102

オリジナルのコードのとおり、普通に

console.log(a) // 12

と書いてしまったら、さすがにそれ以上どうしようもないので、せっかくなのでLog自体もリアクティブに紐づけています。

const Log = a['>='](log);

こういう式を定義しておくことで、Logは恒久的にリアクティブ値である a にリアクティブに反応してlogを書き出し続けます。従って、この式の後で、

b['>'](next(100));

と、これもリアクティブ値である b を更新すると、リアクティブに 102 とコンソールに書き出します。 23.2. ReactiveFunctor ReactiveMonadこのFRP実装は、非常に強力です。逆にいくら関数型プログラミングの理論を突き詰めても、つまるところ、このようにログであるとか、実世界と時間依存するようなコードが書けなければ、事実上実用的なアプリケーションは何一つ書くことはできないでしょう。まさに関数型プログラミングが机上の空論で終わってしまいます。 そしてこのFRP実装は極めてシンプルで、使い方は極めてシンプルです。その理由は、このFRPが、あるひとつのFunctorあるいはMonadで、ただの代数構造でしかないからです。 このFRPはたかだかひとつのFunctorとして実装されていて、同時にMonadとしても実装されています。二項演算であり、二項演算子は>=というシンボルで表現されています。タイプコンストラクタは、IOであり、

const b = IO(1);const c = IO(2);

このように、リアクティブ値を構築します。Monadなので、このタイプコンストラクタ IO は、この二項演算の左右の単位元としても機能します。 二項演算の左のオペランドは、リアクティブ値、つまり、a,b,c,Logとここで定義されている全ての値で

const Log = a['>='](log);

右オペランドは、Functor/Monadなので、当然こういうLogなどの関数です。

['>='](([b, c]) => b + c);

というように、リアクティブに演算を行う関数の場合もあります。このオリジナルの仮想コード

var a $= b + c

に該当する

const a = allNoResetIO([b, c]) ['>='](([b, c]) => b + c);

は、2つのリアクティブ値が更新されたときに、まとめて更新されるリアクティブ値をアウトプットにする関数で、このコードでは、二項演算の左のオペランドになっています。 allNoResetIOと長ったらしい命名にしているのは、この「リアクティブ値をまとめる」というやりかたは別にひとつでなく複数のパターンがあり、他にも、allAndResetIOがあります。これらの長い名前の、まとめる系の関数は、ReactiveMonadとは別の関数として実装されています。こういうシンプルなDemoでも、リアクティブ値をまとめる系の関数はかなり必要となるので、別途実装しています。 コアとなるReactiveFunctorとReactiveMonadはその名の通りの二項演算でしかないので、原理的に複雑になりようもありませんが、別途このようにプラグイン的に必要な関数があれば、コアとなるReactiveMonadを利用して、目的の用途に応じて実装していきます。 実際に、allNoResetIOallAndResetIO関数は、ReactiveMonadを利用して実装されています。 その意味では、ReactiveMonadに依存するFRPライブラリを構成すると言えなくもないですが、別に誰かが発明した仕様が難解なAPIがズラリとそろっている学習するのが困難なFRPフレームワークではありません。 そして、もしその必要を感じるのであれば、多数の関数を準備することで高度なFRPフレームワークぽくすることも可能です。究極的には依存しているのは、ReactiveMonadひとつだけ、というシンプルでミニマルでありながら強力なFRPです。 ちなみにこういう、関数型コードでは結構シンプルにまた無駄なくエレガントにただひとつの代数構造であるFunctorやMonadで実装できるようなFRPでも、オブジェクト指向では、モデル-ビュー-コントローラー（MVC）アーキテクチャーがこういう役割分担になっていてデータバインディングがあってビューは自動的に更新される、、、などとやっていますが、非常に冗長で筋が良くないですね。 23.3. ReactiveFunctor を実装するための下敷きとなるアイデアReactiveFunctorを実装すれば、その延長線上でReactiveMonadも実装できますから、なにはともあれまず最初にFunctorを実装する必要があります。逆にそれが終われば8割がたの仕事は終わりです。 Demoあるいは、オリジナルの仮想リアクティブコードを見ていてもすぐわかりますが、これは要するにExcelなどの表計算ソフトの挙動と同じです。 表計算ソフトのセルは依存グラフのかたまりです。

AとBの2つのセルに注目します。ITリテラシがある現代人にとっては結構見慣れた光景かもしれません。Aのセルを更新すれば、自動的にBのセルも更新される、これはまさにリアクティブプログラミングそのものです。そして、1. Aはリアクティブ値2. Bに関数 f が入った結果、3. Bの値がリアクティブに更新されるということなので、これを数式で考えると、Aとfの間の二項演算となっているFunctorです。B = A ⩾ fつまり、配列でB = A.map(f)とやっているのと変わりません。 そしてこの延長線上で、おなじように、

今度は、AとCのセルに注目します。C = A ⩾ gという同じ構造ではあるが別の二項演算になります。 ここでもうトリックはわかりました。Aというセルを起点に考えて A ⩾ fA ⩾ g と複数の任意の関数がどんどん登録され積み上がっていって、そのそれぞれの二項演算の結果、B = A ⩾ fC = A ⩾ gという、別のリアクティブ値が生成されていくのだろうと。 Aには、無限リストとして、[f, g, h, ..........]のように登録された関数が追加されていて、登録時には、新規に生成されたセル B, C, Dがある。 そして、セルAの値が更新されたら、Aのリストに登録されている関数を一斉に、その更新値をもって関数適用して、その結果はB,C,Dに送られる、そしてそのそれぞれのB,C,D自体も、Aと同様にリアクティブなセルなので、それぞれのリストに登録されたすべての関数が送られた更新値をもって一斉に関数適用、、、とこういうカラクリなのでしょう。 というより、もしかしたら、表計算ソフトの利用者の多くは直感的に理解している仕組みを繰り返しているだけなのかもしれません。 23.4. ReactiveFunctor を実装するスタート地点 B = A ⩾ fというのは、B = A > map(f)であったように、B = A > reactive(f)なので、ReactiveFunctorの実装としては、このreactive関数を実装することになります。 mapFunctorについてはすでにかなりよく調べており、実装についても詳細に判明しています。

Functorをもっと厳密にTypeScriptで定義していく type F<A> = A[];const F = // type constructor <A>(a: A): F<A> => [a]; type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0])); const f = (a: number) => a * 2; const A = F(1); // [1] type constructconst B = P(A)['>'](map(f));// [2] mapped このコードでは概念をかんたんに示す目的のために「1要素だけの配列のmap」を定義しています。 型定義だけを改めて抜粋すると、 type F<A> = A[]; // type constructor type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; このTypeScriptのコードで、かなり正確に、Functorの概念を表現できています。 ちなみに、Haskellでは、型定義にプレースホルダは積み増さない流儀なので、 fmap :: (a -> b) -> f a -> f b とFunctorはよりスッキリと定義されてるのですが、全く同じ意味です。 TypeScriptではプレースホルダは逐一明示したほうが便利だ、という方針で、そのメリットは確かに大きいですが、こういう抽象度が高い概念になると、逆に見通しが悪くなるデメリットはありますね。 視覚的に表現するとこういう概念図になるでしょう。 mapFunctorfmap(f)FunctionFunctionmorphismmorphism

最終的には、このTypeScriptのコードをそのまま参考にして型のコードを書きますが、とりあえず概念のかんたんのために見通しをよくして、JavaScriptだけのコードから立ち上げることにします。 23.5. ReactiveFunctor のタイプコンストラクタ（型構築子）まずはタイプコンストラクタですが、mapFunctorの場合は、 a から [a]というように大変シンプルでした。 ReactiveFunctorのタイプコンストラクタであるIOはいったいどういう構造になるのでしょうか？ 要するに表計算ソフトのセルの実装そのものです。セルの挙動を考えると、

Aには、無限リストとして、[f, g, h, ..........]のように登録された関数が追加されていて

となっていて、素朴な感覚としては、時間軸で刻々と変化する可変長の無限リストの構造です。つまり、永続データ構造（Persistent data structure）　

永続データ構造（えいぞくデータこうぞう、英: Persistent data structure）は、変更される際に変更前のバージョンを常に保持するデータ構造である。このようなデータ構造は、更新の際に元のデータ構造を書き換えるのではなく、新たなデータ構造を生成すると考えられ、イミュータブルなデータ構造の構築に利用可能である。

ですね。 ただし実際に実装するとなると、これは履歴を全部保持するようなバージョニングのデータ構造にする合理性はあるのか？という強い疑念がでてきます。 つまり、表計算ソフトの操作履歴をGitのように全バージョンを保持しておく必要がどこにあるのだろう？ということです。 普通に考えてその必要はないので、最新の履歴、つまり直近の値だけを保持することにします。なんのことはない、Mutableなデータですが、あくまで概念的にはImmutableで最新、直近の値にアクセスしている、ということにします。 Mutableな値で問題となるのは、根本的に依存グラフを構成していないからです。依存グラフで「管理」もされていない値が時間軸で変化していくのは非常に良くないですが、最新の値が常に依存グラフの一部である場合は、なんの問題も発生しない、ということになります。 そしておそらくこういうトリックを使うのは、こういうIOのFunctorを実装するときに限られるでしょう。なぜならば、これ以降で同じことをしたい場合は、このIOのFunctorがすでに手元にあるので、それを使えば良くて、それでImmutableなデータ構造とみなせるからです。 今、時系列の方向の履歴の無限リストを考えていましたが、[f, g, h, ..........]のように登録された関数のリストそれ自体は、最新の値に限定したとしもリストになっているはずです。 ここで方法は２つ考えられて、ひとつめは、そのとおり素直に配列として実装する。ふたつめは、

セルAの値が更新されたら、Aのリストに登録されている関数を一斉に、その更新値をもって関数適用して、その結果はB,C,Dに送られる

ということなので、もうそのリストの関数を1つの関数に合成してしまって、その合成された関数1個だけを最新の値として保持する、ことが考えられます。 どちらが良いのか？実装に迷うところですが、おそらくデータのあり方としてシンプルで堅牢なのは、リストの保持ではなくて、1つだけの関数の保持でしょうし、関数合成というのは二項演算なので間違う要素が少ないし、間違ったらすぐ検出できそうです。リストの取り扱いで間違ったら原因究明で厄介なことになりそうだ、という直感が働きます。 ふたつめの、「リストの関数を1つの関数に合成してしまって、その合成された関数1個だけを最新の値として保持する」というアプローチを選択します。 reactiveFunctorのタイプコンストラクタ

const IO = () => P({ lastF: identity //mutable }); //now pipeline-operator available to IO

lastFという要素があるオブジェクトがReactive値で、それを生成するタイプコンストラクタIO関数です。まずは、極力シンプルに保つためにインプットもありません。 最初に保持している関数はidentityです。何もしない関数で、関数の単位元を保持していることになります。なにかを実装するときに、自然とこういう単位元が必要になってくるのは設計として良い兆候です。 reactiveFunctorのReactive値は、パイプライン演算が使えてほしいので、予めもうここでP関数でくるんでいます。今後もうreactiveFunctorのReactive値ならば自動的にパイプライン演算が使えます。 タイプコンストラクトして、セルAを作り出します。

const A = IO();

パイプライン演算が使えるはずなので確認しておきます。

A['>'](log);

{ lastF: [Function: identity] }

23.6. ReactiveFunctor の二項演算子を表すreactive関数①

B = A ⩾ fというのは、B = A > map(f)であったように、B = A > reactive(f)なので、ReactiveFunctorの実装としては、このreactive関数を実装することになります。

mapFunctorについてはすでにかなりよく調べており、実装についても詳細に判明しています。

Functorをもっと厳密にTypeScriptで定義していく type map = <A, B> // function => function (f: (a: A) => B) => (Fa: F<A>) => F<B>; const map: map = <A, B> (f: (a: A) => B) => (Fa: F<A>): F<B> => F(f(Fa[0])); 視覚的に表現するとこういう概念図になるでしょう。 mapFunctorfmap(f)FunctionFunctionmorphismmorphism

これが一番外側のアウトラインです。 JavaScriptのコードをみると、結構単純ではあって、

const map = f => Fa => F(f(Fa[0]));

mapFunctorは二項演算でmap演算子を定義する　mapの左右のオペランドがある左オペランドは Fa右オペランドは f両方のオペランドが満たされたときには、新しいFbをタイプコンスタクタ F で構築しながらアウトプットする そういうことです。これをreactiveFunctorに置き換えたいのですが、

AとBの2つのセルに注目します。ITリテラシがある現代人にとっては結構見慣れた光景かもしれません。Aのセルを更新すれば、自動的にBのセルも更新される、これはまさにリアクティブプログラミングそのものです。そして、1. Aはリアクティブ値2. Bに関数 f が入った結果、3. Bの値がリアクティブに更新されるということなので、これを数式で考えると、Aとfの間の二項演算となっているFunctorです。B = A ⩾ fつまり、配列でB = A.map(f)とやっているのと変わりません。

というアイデアを念頭において、 reactiveFunctorは二項演算でreactive演算子を定義する　reactiveの左右のオペランドがある左オペランドは セルA右オペランドは 登録したい関数 f両方のオペランドが満たされたときには、新しいセルBをタイプコンスタクタ IO で構築しながらアウトプットする 従って、

const reactive = f => A => IO()['>'](B => B); // new IO created // A['>'](reactive(f)) returns new B

？？となるかもしれませんが、

IO()['>'](B => B); // new IO created

IO() でタイプコンストラクトして、B⟹B のidentity関数をパイプライン演算で適用しているだけなので、そのままIO()が出てきます。 新しいセルBをタイプコンスタクタ IO で構築ということをやっており、そのBに関してAで関数fについて登録する、という作業はなにもやっておらず、(B => B)とだけやっています。ここはあとでやります。

const f = a => a * 2; const B = A['>'](reactive(f)) B['>'](log);

{ lastF: [Function: identity] }

新しいセルBが、Aとfのreactive二項演算によって生み出されて返ってきました。これで、とりあえず、• IOタイプコンストラクタと• reactive演算子とFunctorの構造をもって最低限の機能をすることが確認できました。　 まずはとりあえずエラーを出さずにちゃんと想定どおり機能するか確認して、そこから徐々に拡張するのが重要です。最初からいきなり複雑なことをやってエラーが出るのが当たり前の状況から削っていく、という開発手法ではうまくいきません。 23.7. ReactiveFunctor のトリガー関数 change() Demoコードで、

const b = IO(1);const c = IO(2); const a = allNoResetIO([b, c]) ['>='](([b, c]) => b + c); b['>'](next(10));const Log = a['>='](log); // 12b['>'](next(100)); // 102

12102

というのを出しましたが、この

b['>'](next(10));

という、reactive値をトリガーする関数を定義します。demoでは最終的なMonadバージョンを使っていて、このトリガー関数の名前が next となっているのですが、Functorバージョンではchangeという名前にしています。 セルAにたいして、

A['>'](change(10));

というように、 トリガー関数は、• セルに入る値つまりreactive値になる値• セル２つのインプットがあるカリー化された高階関数です。

const change = a => A => right (A.lastF(a)) //apply new a to the composed function (A);

最終的に、セルAがそのまま返ってきてほしいので、

　　　right (A.lastF(a)) //apply new a to the composed function (A);

right関数を利用してこのような形になっており、ほんとうにやりたいのは、

(A.lastF(a)) //apply new a to the composed function

で、Aに登録されている最新の関数である、A.lastFに対して、reactive値を適用しています。ここで注意したいのが、このA.lastF(a)関数適用の返り値はそのままright関数によって捨てられてしまう、ということです。Aに登録された関数のリストが合成されていて、そのすべてに a で適用したいというだけで、返り値は求めていません。これは

命令型では普通にやっている、文（Statement）の上下の羅列による順次実行と全く同じことです。たとえば、right関数を利用したlog関数 const log = a => 　　　　　　　right　　　　　　　　(console.log(a))　　　　　　　　(a); は、 const log = a => { console.log(a); return a;}; という命令型のコードを書いているのと全く同じです。関数型コードでも、たとえば、特に、本書であとからやるFRPの実装では、原理的にIOを弄り倒すので、そういうIOと関与しない範囲の関数型コードではアンチパターンである、このような命令型の列挙をしたくなる局面が非常に多いのです。そこで諦めて｛｝を使って、冗長なreturn文（Statement）などを書きたくない場合は、right関数を利用することで、あくまで式（Expression）としてスッキリと書き下すことが可能になります。

と一緒で、リストにあるすべての値について、同じ関数を適用させたい、それだけ、ということで、それぞれの返り値について、別途きちんと処理することにします。 23.8. ReactiveFunctor の二項演算子を表すreactive関数②一番外側の構造

const reactive = f => A => IO()['>'](B => B); // new IO created // A['>'](reactive(f)) returns new B

の続きです。

(B => B)

を

(B => // new IO created right (A.lastF = //mutable F(A.lastF)['.'] //function composition (a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions ) )(B))

で置き換えます。一気に複雑になりましたが、外側から説明していきます。

(B => // new IO created right (　 )(B))

で、最終的には、最初の設計どおりBを返しています。rightの左側は捨てられてしまいます。その捨てられるrichtの左側は、

　　　　　　　A.lastF = //mutable F(A.lastF)['.'] //function composition (a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions )

で、これも外側からいくと、

　　　A.lastF = F(A.lastF)['.'] (　 )　　//function composition

となっていて、A.lastF を 新しい関数

　　　　F(A.lastF)['.'] (　 )　　//function composition

で上書きしています。ここでは、既存のA.lastF という直近の関数と ( ) の中の関数を合成（連結）しています。この関数合成演算子は、ローカル関数合成演算子を与えるF関数により与えられています。

関数の合成演算はモノイドなので、F関数を使ったローカル拡張 F(f)['.'](g) となっているのは、結構気持ち悪くて、素直に、Function.prototypeのグローバル拡張 (f)['.'](g) とシンプルに表現しておきたいです。 ただし、あとから実装するFRPライブラリでは、ライブラリなのでグローバルスペースに干渉するのは良くないので、自己完結しておくために、このローカルアプローチを採用しています。（どうせ関数合成は1箇所しか使っていない）

この（どうせ関数合成は1箇所しか使っていない）というのがこの部分です。ここがちょうど、

ふたつめの、「リストの関数を1つの関数に合成してしまって、その合成された関数1個だけを最新の値として保持する」というアプローチを選択します。

に該当。( ) の中の関数は、　

　　　　　　　 (a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions )

ここも　right関数で、左のインプットは捨てられるので、外側は、

　　　　　　　 (a => a) 　

というidentity関数が合成されている、ということになります。A.lastFの値はもともとがidentity関数だったので、

　　　　F(identity)['.'](identity)　　//function composition

となっています。つまり、A.lastFは、タイプコンストラクタ

const IO = () => P({ lastF: identity //mutable }); //now pipeline-operator available to IO

の最初からずっと一貫して外側から見ると identity関数のまま、ということです。捨てられた左のインプットは、

　　　　　　　B['>'](change(f(a)))　//a applied to all reactive functions

で、ようやく一番内側までたどり着くことができました。これは、まさに、

ReactiveFunctor のトリガー関数 change()　セルAにたいして、 A['>'](change(10));

というトリガー関数で、セルBにむけてリアクティブ値をトリガーしろ、ということです。外側は、

　　　　　　　 (a => a) 　

というidentity関数だったのですが、実はこの a は、

　　　　　　　 (a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions )

のとおり、未来のreactive値なので、そういう構造が組み入れられた上で、関数合成されて新しいA.lastFという直近の合成関数として登録された、ということになります。たしかにrightの左側は捨てられるのですが、

最終的に、セルAがそのまま返ってきてほしいので、 　　　right (A.lastF(a)) //apply new a to the composed function (A); right関数を利用してこのような形になっており、ほんとうにやりたいのは、 (A.lastF(a)) //apply new a to the composed function で、Aに登録されている最新の関数である、A.lastFに対して、reactive値を適用しています。ここで注意したいのが、このA.lastF(a)関数適用の返り値はそのままright関数によって捨てられてしまう、ということです。Aに登録された関数のリストが合成されていて、そのすべてに a で適用したいというだけで、返り値は求めていません。これは 命令型では普通にやっている、文（Statement）の上下の羅列による順次実行と全く同じことです。たとえば、right関数を利用したlog関数 const log = a => 　　　　　　　right　　　　　　　　(console.log(a))　　　　　　　　(a); は、 const log = a => { console.log(a); return a;}; という命令型のコードを書いているのと全く同じです。関数型コードでも、たとえば、特に、本書であとからやるFRPの実装では、原理的にIOを弄り倒すので、そういうIOと関与しない範囲の関数型コードではアンチパターンである、このような命令型の列挙をしたくなる局面が非常に多いのです。そこで諦めて｛｝を使って、冗長なreturn文（Statement）などを書きたくない場合は、right関数を利用することで、あくまで式（Expression）としてスッキリと書き下すことが可能になります。 と一緒で、リストにあるすべての値について、同じ関数を適用させたい、それだけ、ということで、それぞれの返り値について、別途きちんと処理することにします。

これと全く同じ構造であることに注目してください。rightの左側は捨てられますが、逐次処理と一緒で「実行」はされるのです。 このような外側はidentity関数である関数が、reactive演算が行われるたびに、どんどん積み増される形で関数合成されて追加されていきます。これがこのreactiveFunctorのコアのコア、中枢であると言えます。 23.9. 初歩的なReactiveFunctor のコードこれで最初の初歩的なReactiveFunctorは完成しました。 ReactiveFunctor

const IO = () => P({ lastF: identity //mutable });//now pipeline-operator available to IO const reactive = f => A => IO()['>'](B => // new IO created right (A.lastF = //mutable F(A.lastF)['.'] //function composition (a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions ) )(B) );// A['>']reactive(f) returns B const change = a => A => right (A.lastF(a)) //apply new a to the composed function (A);

23.10. 初歩的なReactiveFunctor のテストテスト

{ const A = IO(); const B = A['>'](reactive(log)); A['>'](change(1)); }

1

成功カラのセルAを定義して、セルAに1を入れました。このセルAに何か値が入ったときに、値をlogしてくれるような新しいセル Bを定義しました。実際にセルAに1を入れたら、期待したとおり値1がlogされました。 テスト

{ const A = IO(); const B = A['>'](reactive(log)); const C = A['>'](reactive(log)); A['>'](change(5)); }

55

成功同じように、セルBとCを、Aに紐付ける形で定義しました。Aに5を入れたときに、セルBとCは双方とも、5をlogしました。 テスト

{ const A = IO(); A['>'](change(1)); const B = A['>'](reactive(log));}

失敗カラのセルAを定義して、その直後にセルAに1を入れました。その後から、Aに何か値が入ったときに、値をlogしてくれるような新しいセル Bを定義しました。結果なにもlogしてこなかったです。 しかし、最初のテスト

{ const A = IO(); const B = A['>'](reactive(log)); A['>'](change(1)); }

1

成功だったのです。 このように、同じ内容なのに、コードの順番が入れ替わっただけで、成功したり失敗するのはよくありません。コードの並び順そのもので依存グラフが変わってしまっている、ということになるからです。言い換えると、コードの並び順によってはFunctorの挙動が「等しくない」ということになり、複雑性が生じています。 従って、このreactiveFuncorの初期バージョンは安全な水準には到達していないと評価します。改善が必要です。 最後のテストが成功することを目指します。そうすれば、少なくともこの範囲においてコードの並び順に関わらずFunctorの挙動が「等しい」ことが確認され、このレベルの複雑性は消滅します。 24. より安全なReactiveFunctor version224.1. やはりReactive値を保持する必要があった初期バージョンが失敗した理由は、Reactive値を保持していなかったことが原因です。あえて過度にシンプルに設計したからです。 24.2. ReactiveFunctor version 2ReactiveFunctor ver.2

const IO = a => P({ lastF: identity, //mutable lastVal: a //mutable }); const reactive = f => A => IO(undefined)['>'](B => // new IO created right (A.lastF = //mutable F(A.lastF)['.']( //function composition a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions ) )(B['>'](change(f(A.lastVal)))) // instant );// A['>']reactive(f) returns B const change = a => A => right( right (A.lastVal = a) //mutable (A.lastF(a)) //apply new a to the composed function )(A);

24.3. タイプコンストラクタタイプコンストラクタは、

const IO = a => P({ lastF: identity, //mutable lastVal: a //mutable });

となりました。 新たに、lastValとしてreactive値が保持されるようになっています。そしてこれはまったく同じ理屈と理由でmutableです。同時に、タイプコストラクタは初期値をインプットとして受け入れるようになりました。24.4. reactive関数

const reactive = f => A => IO(undefined)['>'](B => // new IO created right (A.lastF = //mutable F(A.lastF)['.']( //function composition a => //a is the future reactive value right (B['>'](change(f(a)))) (a) //a applied to all reactive functions ) )(B['>'](change(f(A.lastVal)))) // instant );// A['>']reactive(f) returns B

reactive関数の一番外側のrightの右側では、単に B を返していたものが、

　(B['>'](change(f(A.lastVal)))) // instant

を返すように変更されました。change関数はトリガーしても、外側は同じくright関数によるidentity関数なので結局はBが返されます。左側で、返り値としては捨てられる、逐次処理は、

change(f(A.lastVal)) // instant

であり、これはreactive演算が行われて、新しいセルであるBが構成されると同時に、登録した関数 f はその場で即座にトリガーされる、という仕組みです。 24.5. change関数

const change = a => A => right( right (A.lastVal = a) //mutable (A.lastF(a)) //apply new a to the composed function )(A);

reactive値を保持するようになったのでトリガーされたときには、登録関数が実行される前に、まずはセルA自身のreactive値がA.lastVal = aと更新されます。 24.6. version2のテスト テスト

{ const A = IO(1); const B = A['>'](reactive(log)); }

1

成功初期値をもって定義したAに対して、二項演算を行ってBが生成されるのと同時に、右オペランドであるlogが即時トリガーされています。 テスト

{ const A = IO(1); const B = A['>'](reactive(log)); A['>'](change(5)); }

15

成功さらに5をトリガーすると、想定通りの挙動を示します。 テスト

{ const A = IO(1); A['>'](change(5)); const B = A['>'](reactive(log)); }

5

成功version1では失敗していたケースです。verison2の最初のテスト

{ const A = IO(1); const B = A['>'](reactive(log)); }

1

でも成功していたのですが、いずれにせよどのタイミングであっても、二項演算により新たなBが生成されると同時に、右オペランドの関数は即時トリガーされます。 ReactiveFunctor version2は直感的にも自然な振る舞いであり、version1の安全ではない問題点は解消されたので、水準を満たすと評価します。 25. ReactiveFunctor version3 (typed with None)25.1. Noneの導入version3ではversion2 にNoneを追加します。 ReactiveFunctorの二項演算対象となる左オペランドの集合に、新たにNoneが追加されます。 B = A ⩾ fA はReactiveFunctorの二項演算対象となる左オペランドの集合 • version2 A: JavaScriptの値すべて• version3 A: JavaScriptの値すべて + None となります。 なぜこんなことをするのか？というと、ReactiveFunctorは、表計算ソフトのセルをモデルとしているのですが、

セルには、JavaScriptの値すべてが入ることを想定しています。この前提で考えると、ではこのセルが空欄である状態は、どうやって表現するのか？という問題が生じます。 「JavaScriptの値すべて」が、セルの空欄でない値なのだから、セルが空欄であるJavaScriptの値は存在しません。従って、新たに1個、このReactiveFunctorの演算にとってReactive値はカラになっているという値を用意する必要があります。 念の為ですが、空の値とは単位元とは異なります。たとえば、flatMapMonadでは、空の値は [ ]　で、左右の単位元はタイプコンストラクタa ⟹ [a]でした。 こういう、演算と空の値については、パイプライン演算子の実装で論じました。

null問題とオプション型（OptionType） ただしいずれのケースにおいても任意のJavaScriptの値にパイプライン演算子を実装するには、undefinedとnullの問題があります。念の為ですが、言語組み込みでパイプライン演算子を実装する際には、コードで表記されているパイプラインを既存の関数適用のして解釈しなおせばよい、SyntaxSugaarでさえあればよい、Macroでも何でも良いですが要するに単にコード上の表記に限る問題なので、何の問題もありません。そういう言語ベースでの実装ならば何の問題もないものを言語ベースでないユーザランドで実装する際に問題が出るので厄介なわけです。 nullはJavaScriptにおいて例外的で特殊なオブジェクトですがメソッドを追加できません。エラーが出ます。またundefinedもオブジェクトで包むObject(undefined)としても、{}と空オブジェクトになり、意味が異なってしまいます。 実際これはソフトウェア開発でよく知られた問題で、一般的にはヌルポインタの問題が著名です。 2009年にアントニー・ホーアは、彼が1965年にALGOL Wの一部としてヌル参照を発明したと述べている。2009年のカンファレンスでホーアはこの発明を「10億ドルの誤り」と述べた。 それは10億ドルにも相当する私の誤りだ。null参照を発明したのは1965年のことだった。当時、私はオブジェクト指向言語 (ALGOL W) における参照のための包括的型システムを設計していた。目標は、コンパイラでの自動チェックで全ての参照が完全に安全であることを保証することだった。しかし、私は単にそれが容易だというだけで、無効な参照を含める誘惑に抵抗できなかった。これは、後に数え切れない過ち、脆弱性、システムクラッシュを引き起こし、過去40年間で10億ドル相当の苦痛と損害を引き起こしたとみられる。 ただしこれは空の値をプログラミング言語がどのように実装しているか？によって別にヌルポインタに限らず問題の出方は様々で、根本的には、実装されている演算子と特殊な空の値の親和性、互換性がなく、演算が破綻する、タイプの不一致の問題です。 では、どのようなアプローチが正解か？というと、空の値であっても明示的に、その演算が対象とするオペランドの型、あるいは集合、別の言い方では、その関数の定義域に含めれば良いわけです。 このアプローチは、オプション型（Option type）としてよく知られています。 In programming languages (especially functional programming languages) and type theory, an option type or maybe type is a polymorphic type that represents encapsulation of an optional value; e.g., it is used as the return type of functions which may or may not return a meaningful value when they are applied. It consists of a constructor which either is empty (often named None or Nothing), or which encapsulates the original data type A (often written Just A or Some A).A distinct, but related concept outside of functional programming, which is popular in object-oriented programming, is called nullable types (often expressed as A?). The core difference between option types and nullable types is that option types support nesting (Maybe (Maybe A) ≠ Maybe A), while nullable types do not (String?? = String?). プログラミング言語（特に関数型言語）や型理論において、オプション型またはmay型は、オプション値のカプセル化を表す多相型である。例えば、関数を適用したときに意味のある値を返すかどうかわからない関数の戻り値の型として使用される。この型は、空であるか（NoneまたはNothingと呼ばれることが多い）、または元のデータ型Aをカプセル化する（Just AまたはSome Aと呼ばれることが多い）コンストラクタで構成されます。関数型プログラミングとは別の概念ですが、オブジェクト指向プログラミングでよく使われる関連概念として、Nullable type（しばしば A? と表記される） オプション型とヌルアブル型の主な違いは、オプション型はネストをサポートしている（Maybe (Maybe A) ≠ Maybe A）のに対し、ヌルアブル型はサポートしていない（String??? = String?） JavaScriptにおいても、実は、オプショナルチェーン (?.) (optional chaining)なるものが実装されていて、 ?. 演算子の機能は . チェーン演算子と似ていますが、参照が nullish (null または undefined) の場合にエラーとなるのではなく、式が短絡され undefined が返されるところが異なります。関数呼び出しで使用すると、与えられた関数が存在しない場合、 undefined を返します。 と、JavaScriptオブジェクトのメソッドチェーンにおいて、それなりにオプション型（Option type）の機能もネイティブに存在していることがわかります。 ただし残念ながら今回のパイプライン演算子の実装には役立たないので、素のJavaScriptの値をオプション型に拡張すると見做し、Noneというパイプライン演算子と互換性のある値を新たに添加する方針で行きます。

ちょうど都合よく、パイプライン演算子でNoneを導入していますから、それを共有できます。 表計算ソフトのセルが空であるとき、なんの挙動も発生しないことは保証されています。ReactiveFunctor ver.3では、Noneが入力された際には演算は行わない、という保証がある仕様にします。 実際に、ReactiveFunctor ver.2では、

const reactive = f => A => IO(undefined)['>'](B => // new IO created

と新たにBを構成する際の初期値にとりあえずなんの理論的な後ろ盾もなく勝手にundefinedを入れていました。 version3では、ここにはNoneが入ります。 25.2. 型（Type）の導入version3はTypeScriptで記述されています。 ReactiveFunctor ver.3

const isNone = <A>(x: A | None): x is None => x === None; const optionMap = <A, B> (f: (a: A) => B) => (a: A) => isNone(a) ? None : f(a); const typeIO = Symbol("IO"); type IO<A> = { lastF: (a: A) => A;// identity Type in outer shape lastVal: A;} & P<any>//circular reference & { ">": <B>(f: (a: A) => B) => P<B> } & { ">>": <B>(f: (a: any) => B) => IO<B> }; const IO = <A>(a: A) => (P({ lastF: identity, //mutable lastVal: a //mutable }) ['>'](customType(typeIO)) ['>'](customOperator('>>')(reactive)) ) as IO<A>; const reactive = <A, B> (f: (a: A) => B) => (A: IO<A>) => IO(None)// new IO created ['>']((B: IO<B>) => //new B right (A.lastF = //mutable F(A.lastF)['.']( //function composition (a: A) => //a is the future reactive value right//type check of A done with optionMap (B['>'](change(optionMap(f)(a)))) (a)//a applied to all reactive functions ) ) (B['>']( change(optionMap(f)(A.lastVal)) )) // instant );// A['>']reactive(f) returns B const change = <A>(a: A) => (A: IO<A>) => right( right (A.lastVal = a) //mutable (optionMap(A.lastF)(a)) )(A); //apply new a to the composed function//return A

25.3. reactive演算子の追加　version2

const B = A['>'](reactive(log));

の表記方法はそのままversion3でも有効に継承されていますが、冗長なのでreactive演算子が追加されています。version3

const B = A['>>'](log);

と書けるようになります。簡潔な表記は大変重要です。 25.4. タイプコンストラクタ

const typeIO = Symbol("IO"); type IO<A> = { lastF: (a: A) => A;// identity Type in outer shape lastVal: A;} & P<any>//circular reference & { ">": <B>(f: (a: A) => B) => P<B> } & { ">>": <B>(f: (a: any) => B) => IO<B> }; const IO = <A>(a: A) => (P({ lastF: identity, //mutable lastVal: a //mutable }) ['>'](customType(typeIO)) ['>'](customOperator('>>')(reactive)) ) as IO<A>;

version2の構造をほぼそのまま継承してTypeScriptで書いているだけですが、上記のとおり、reactive演算子が追加されています。

['>'](customOperator('>>')(reactive))

さらに

['>'](customType(typeIO))

と、IO型であることを明示しました。

const typeIO = Symbol("IO");

const customType = (type: symbol) => <T>(set: T) => Object.defineProperty(set, type, { value: type });

これは、Monadにするための布石です。flatの機構を実装するためには、Typeの判定が必要になってくるからです。そして、実はこのcustomType関数は、パイプラインMonad演算子の実装でも使いました。 25.5. isNoneとoptionMap

const isNone = <A>(x: A | None): x is None => x === None; const optionMap = <A, B> (f: (a: A) => B) => (a: A) => isNone(a) ? None : f(a);

ReactiveFunctor ver.3では、Noneが入力された際には演算は行わない、という実装がここです。ver,3のすべての関数適用はoptionMapを通じて行われており、isNoneで判定しています。 reactive, change関数では、この該当部分だけoptionMap関数に置き換えられています。reactive, change関数は、それ以外の変更箇所はなく、typeをつけただけで特に追加の説明はありません。25.6. version3のテストテスト

{ const A = IO(None); const B = A['>>'](log); A['>'](change(7)); A['>'](change(None)); A['>'](change(undefined)); A['>'](change(null)); }

7undefinednull

成功reactive値がNoneでトリガーされたときだけ、Functorの演算はなされず出力されていません。初期値についても同様です。 その他の挙動についてはversion2と全く同じなのでテストは省略します。 26. ReactiveMonad26.1. flat機構の追加ReactiveMonadでは、ReactiveFunctor version3 にflat機構を追加します。

Monadの実装にはflatという概念が使われているflatMapMonadの実際の実装は、 const flatMap: flatMap = <A, B> (f: (a: A) => F<B>) => (Fa: F<A>): F<B> => Fa.map(f).flat() as F<B>; Fa.map(f) の値を、flat() している、と結構単純なものになっています。 Array.flatMapのタイプコンストラクタは const F = // type constructor a => [a]; こういう[]を積み増す方向の関数であり、逆にArray.flat()は、1階層分の構造を潰す（平坦化する）方向の関数です。Array.prototype.flat()からサンプルコードをそのまま引用すると、 const arr1 = [0, 1, 2, [3, 4]];console.log(arr1.flat());// expected output: [0, 1, 2, 3, 4] const arr2 = [0, 1, 2, [[[3, 4]]]];console.log(arr2.flat(2));// expected output: [0, 1, 2, [3, 4]] どういうMonadであっても、そのタイプコンストラクタで構築される構造があり、そのMonad演算の演算子の関数では、必ずその逆方向に平坦化する操作が行われます。 タイプコンストラクタは、unitと呼ばれることも多く、flatと合わせて語呂も良いので合わせて図式化してみると、 • unit(タイプコンストラクタ) は１階層だけ上げる。　• flat はネストしていれば１階層だけ下げる。 という構造になっていて、どんなMonadのflatに該当する操作でも、せっかく構築した型（Type）を破壊して、素の値がでてくるまでflatしてしまうことはありません。 [[7]].flat() // [7][7].flat() // [7] このように、Array.flat は、もし Array がネストしてたら、１階層下げて Array を返しますが、ネストしていなかったらそのままの Array を返します。最後の配列の皮を剥いで、裸の値 7 を返すようなことはありません。つまり、Array.flat の返り値は必ず Array タイプである、という基底が保証されている安全な関数です。

Array.flatMapというMonadが、Array.mapというFunctorにflat機構を加えて成されているのと同様に、IO.changeに change関数　 ReactiveFunctor ver.3 からそのまま継承

const change = <A>(a: A) => (A: IO<A>) => right( right (A.lastVal = a) //mutable (optionMap(A.lastF)(a)) )(A); //apply new a to the composed function

flatChange関数　ReactiveMonadで追加されたflat機構

const flatChange = <A>(a: A) => (A: IO<A>) => typeIO in Object(a) 　//flat TTX=TX ? A['>'](change((Object(a) as IO<A>).lastVal)) : A['>'](change(a));

flatChangeという名前が長いので next というショートカットを追加

const next = flatChange;

ここで、• flat はネストしていれば１階層だけ下げる。という実装が、

typeIO in Object(a) 　//flat TTX=TX ? A['>'](change((Object(a) as IO<A>).lastVal)) : A['>'](change(a));

です。 version3のタイプコストラクタで、

さらに ['>'](customType(typeIO)) と、IO型であることを明示しました。 const typeIO = Symbol("IO"); const customType = (type: symbol) => <T>(set: T) => Object.defineProperty(set, type, { value: type }); これは、Monadにするための布石です。flatの機構を実装するためには、Typeの判定が必要になってくるからです。そして、実はこのcustomType関数は、パイプラインMonad演算子の実装でも使いました。

と説明されている仕様に該当します。

typeIO in Object(a)

で、typeIOがオブジェクトのプロパティにあれば、それはIO型であるということが判定できます。IO型の値をそのままchangeでトリガーすると、ネストしたIO型になってしまうので、

? A['>'](change((Object(a) as IO<A>).lastVal))

IO型の中身であるlastValでchangeでトリガーします。もし、値がIO型ではない値であれば、

: A['>'](change(a));

そのままの値 a でchangeでトリガーします。 26.2. flatReactive関数と演算子の追加　ReactiveMonadでは、flatReactive関数と演算子が追加されます。

const B = A['>'](flatReactive(log));

これは追加で割り当てられた二項演算子で書けます。

const B = A['>='](log);

reactive関数　 ReactiveFunctor ver.3 からそのまま継承

const reactive = <A, B> (f: (a: A) => B) => (A: IO<A>) => IO(None)// new IO created ['>']((B: IO<B>) => //new B right (A.lastF = //mutable F(A.lastF)['.']( //function composition (a: A) => //a is the future reactive value right//type check of A done with optionMap (B['>'](change(optionMap(f)(a)))) (a)//a applied to all reactive functions ) ) (B['>']( change(optionMap(f)(A.lastVal)) )) // instant );// A['>']reactive(f) returns B

flatReactive関数　changeをflatChangeに置き換え

const flatReactive = <A, B> (f: (a: A) => B) => (A: IO<A>) => IO(None)// new IO created ['>']((B: IO<B>) => //new B right (A.lastF = //mutable F(A.lastF)['.']( //function composition (a: A) => //a is the future reactive value right//type check of A done with optionMap (B['>'](flatChange(optionMap(f)(a)))) (a)//a applied to all reactive functions ) ) (B['>']( flatChange(optionMap(f)(A.lastVal)) )) // instant );// A['>']flatReactive(f) returns B

26.3. タイプコンストラクタ

const typeIO = Symbol("IO"); type IO<A> = { lastF: (a: A) => A;// identity Type in outer shape lastVal: A;} & P<any>//circular reference & { ">": <B>(f: (a: A) => B) => P<B> } & { ">>": <B>(f: (a: any) => B) => IO<B> } & { ">=": <B>(f: (a: any) => IO<B> | B) => IO<B> }; const IO = <A>(a: A) => (P({ lastF: identity, //mutable lastVal: a //mutable }) ['>'](customType(typeIO)) ['>'](customOperator('>>')(reactive)) ['>'](customOperator('>=')(flatReactive)) ) as IO<A>;

ReactiveMonadはReactiveFunctorの上位互換なので、Fuctorの演算子も継承しており使う事ができます。 26.4. ReactiveMonad 結合性（Associativity）テスト関数とMonadの合成（連結）演算子をそれぞれ定義しておきます。

const compose = <B, C>(g: (b: B) => C) => <A>(f: (a: A) => B) => (a: A) => g(f(a)); const IOcompose = <B, C>(g: (b: B) => C) => <A>(f: (a: A) => B) => P((a: A) => IO(a)['>='](f)['>='](g)); P(Function.prototype)['>'] (customOperator('.') (compose)); P(Function.prototype)['>'] (customOperator('..') (IOcompose));

　テスト

{ const f1 = (a: number) => a * 2; const f2 = (a: number) => a + 1; { const A = IO(1)['>='](f1)['>='](f2); A['>='](log); } {//endofunctor associativity const A = IO(1)['>=']((x: number) => P(x)['>'](f1)['>'](f2)); A['>='](log); const B = IO(1)['>=']((f1)['.'](f2))//function composition B['>='](log); } {//monad associativity const A = IO(1)['>=']((x: number) => IO(x)['>='](f1)['>='](f2)); A['>='](log); const B = IO(1)['>=']((f1)['..'](f2));//monad composition B['>='](log); } }

3[Number: 3]333

成功 テスト

{ const f1 = (a: number) => IO(a * 2); const f2 = (a: number) => IO(a + 1); { const A = IO(1)['>='](f1)['>='](f2); A['>='](log); } { const A = IO(1)['>='](x => IO(x)['>='](f1)['>='](f2)); A['>='](log); const B = IO(1)['>=']((f1)['..'](f2)); B['>='](log); } }

333

成功　 テスト

{　 const f1 = <A>(a: IO<A>) => a['>=']((a: number) => IO(IO(a * 2))); const f2 = <A>(a: IO<A>) => a['>=']((a: number) => IO(IO(a + 1))); const a = IO(1); { const A = IO(a)['>='](f1)['>='](f2); A ['>='](log) ['>='](log); } { const A = IO(a)['>='](x => IO(x)['>='](f1)['>='](f2)); A ['>='](log) ['>='](log); const B = IO(a)['>=']((f1)['..'](f2)); B ['>='](log) ['>='](log); } }

{ lastF: [Function: identity], lastVal: 3 }3{ lastF: [Function: identity], lastVal: 3 }3{ lastF: [Function: identity], lastVal: 3 }3

成功 26.5. ReactiveMonad 左右の単位元（left & right Identity）テスト テスト

{ const f = (a: number) => IO(a * 2); //center f const center = P(1)['>'] ( f ); //left e * f = f const left = P(1)['>'] ( (IO)['..'](f) ); //right f * e = f const right = P(1)['>'] ( (f)['..'](IO) ); left['>='](log); //IO type center['>='](log); //IO type right['>='](log); //IO type }

222

成功 26.6. ReactiveMonad ES Modules（ESM）

import { None, P,//Pipe customType, customOperator, F//Function composition} from "./NonePcustomTypeOperator.js"; const obj = (() => { const identity = <A>(a: A) => a; const right = <A>(a: A) => <B>(b: B) => b; const log = <A>(a: A) => right (console.log(a)) (a); const isNone = <A>(x: A | None): x is None => x === None; const optionMap = <A, B> (f: (a: A) => B) => (a: A) => isNone(a) ? None : f(a); const typeIO = Symbol("IO"); type IO<A> = { lastF: (a: A) => A;// identity Type in outer shape lastVal: A; } & P<any>//circular reference & { ">": <B>(f: (a: A) => B) => P<B> } & { ">>": <B>(f: (a: any) => B) => IO<B> } & { ">=": <B>(f: (a: any) => IO<B> | B) => IO<B> }; const IO = <A>(a: A) => (P({ lastF: identity, //mutable lastVal: a //mutable }) ['>'](customType(typeIO)) ['>'](customOperator('>>')(reactive)) ['>'](customOperator('>=')(flatReactive)) ) as IO<A>; const reactive = <A, B> (f: (a: A) => B) => (A: IO<A>) => IO(None)// new IO created ['>']((B: IO<B>) => //new B right (A.lastF = //mutable F(A.lastF)['.']( //function composition (a: A) => //a is the future reactive value right//type check of A done with optionMap (B['>'](change(optionMap(f)(a)))) (a)//a applied to all reactive functions ) ) (B['>']( change(optionMap(f)(A.lastVal)) )) // instant ); const flatReactive = <A, B> (f: (a: A) => B) => (A: IO<A>) => IO(None)// new IO created ['>']((B: IO<B>) => //new B right (A.lastF = //mutable F(A.lastF)['.']( //function composition (a: A) => //a is the future reactive value right//type check of A done with optionMap (B['>'](flatChange(optionMap(f)(a)))) (a)//a applied to all reactive functions ) ) (B['>']( flatChange(optionMap(f)(A.lastVal)) )) // instant ); const change = <A>(a: A) => (A: IO<A>) => right( right (A.lastVal = a) //mutable (optionMap(A.lastF)(a)) )(A); const flatChange = <A>(a: A) => (A: IO<A>) => typeIO in Object(a) ? A['>'](change((Object(a) as IO<A>).lastVal)) //flat TTX=TX : A['>'](change(a)); const next = flatChange; return { IO, next, typeIO }; })(); type IO<A> = { lastF: (a: A) => A;// identity Type as outer frame lastVal: A;} & P<any>//circular reference & { ">": <B>(f: (a: A) => B) => P<B> } & { ">>": <B>(f: (a: any) => B) => IO<B> } & { ">=": <B>(f: (a: any) => IO<B> | B) => IO<B> }; const IO = obj.IO;const next = obj.next;const typeIO = obj.typeIO; export { IO, next, typeIO }

　 27. ReactiveMonadのエクステンション関数 27.1. DemoReactive programmingのWikipedia項目の前半部分に、FRPのDemoにちょうど良さそうなコードがあるので、それを活用します。コードを引用すると、

var b = 1var c = 2var a = b + cb = 10console.log(a) // 3 (not 12 because "=" is not a reactive assignment operator)

前半は普通の命令型のコードで、一旦、

var a = b + c

と定義というより「代入」したあとで、

b = 10

と、bを「破壊的代入」しても、a の値についてはすでに計算済みなので影響を受けません、という、まずまず命令型プログラマにとっては、常に考える対象となる事柄で、特に工夫のない関数型コードであっても、ある程度共有できるアイデアが説明されています。その後で、長いコメントがあり、

// now imagine you have a special operator "$=" that changes the value of a variable (executes code on the right side of the operator and assigns result to left side variable) not only when explicitly initialized, but also when referenced variables (on the right side of the operator) are changed

ここで、明示的に初期化されたときだけでなく、（演算子の右側で）参照される変数が変更されたときにも、変数の値を変更する（演算子の右側でコードを実行し、その結果を左側の変数に代入する）特殊な演算子「$=」があるとします。

と仮想的なリアクティブ演算子があるという説明があり、その後、その仮想リアクティブ演算子を利用したリアクティブプログラミングのコードがあります。

var b = 1var c = 2var a $= b + cb = 10console.log(a) // 12

まずまずリアクティブというアイデアは理解しやすい、特に命令型コードに慣れ親しんでいるプログラマにとっては、コードの上下のフローが逆行するようなありえないことが実現しているよう見えます。 この仮想的なリアクティブなコードを、今から実装するFRPの実際のコードに書き直します。

const b = IO(1);const c = IO(2); const a = allNoResetIO([b, c]) ['>='](([b, c]) => b + c); b['>'](next(10));const Log = a['>='](log); // 12b['>'](next(100)); // 102

12102

　 27.2. ReactiveMonadとエクステンション関数の関係 このFRP実装は、非常に強力です。逆にいくら関数型プログラミングの理論を突き詰めても、つまるところ、このようにログであるとか、実世界と時間依存するようなコードが書けなければ、事実上実用的なアプリケーションは何一つ書くことはできないでしょう。まさに関数型プログラミングが机上の空論で終わってしまいます。 そしてこのFRP実装は極めてシンプルで、使い方は極めてシンプルです。その理由は、このFRPが、あるひとつのFunctorあるいはMonadで、ただの代数構造でしかないからです。 このFRPはたかだかひとつのFunctorとして実装されていて、同時にMonadとしても実装されています。二項演算であり、二項演算子は>=というシンボルで表現されています。タイプコンストラクタは、IOであり、

const b = IO(1);const c = IO(2);

このように、リアクティブ値を構築します。Monadなので、このタイプコンストラクタ IO は、この二項演算の左右の単位元としても機能します。 二項演算の左のオペランドは、リアクティブ値、つまり、a,b,c,Logとここで定義されている全ての値で

const Log = a['>='](log);

右オペランドは、Functor/Monadなので、当然こういうLogなどの関数です。

['>='](([b, c]) => b + c);

というように、リアクティブに演算を行う関数の場合もあります。このオリジナルの仮想コード

var a $= b + c

に該当する

const a = allNoResetIO([b, c]) ['>='](([b, c]) => b + c);

は、2つのリアクティブ値が更新されたときに、まとめて更新されるリアクティブ値をアウトプットにする関数で、このコードでは、二項演算の左のオペランドになっています。 allNoResetIOと長ったらしい命名にしているのは、この「リアクティブ値をまとめる」というやりかたは別にひとつでなく複数のパターンがあり、他にも、allAndResetIOがあります。これらの長い名前の、まとめる系の関数は、ReactiveMonadとは別の関数として実装されています。こういうシンプルなDemoでも、リアクティブ値をまとめる系の関数はかなり必要となるので、別途実装しています。 コアとなるReactiveFunctorとReactiveMonadはその名の通りの二項演算でしかないので、原理的に複雑になりようもありませんが、別途このようにプラグイン的に必要な関数があれば、コアとなるReactiveMonadを利用して、目的の用途に応じて実装していきます。 実際に、allNoResetIOallAndResetIO関数は、ReactiveMonadを利用して実装されています。 その意味では、ReactiveMonadに依存するFRPライブラリを構成すると言えなくもないですが、別に誰かが発明した仕様が難解なAPIがズラリとそろっている学習するのが困難なFRPフレームワークではありません。 そして、もしその必要を感じるのであれば、多数の関数を準備することで高度なFRPフレームワークぽくすることも可能です。究極的には依存しているのは、ReactiveMonadひとつだけ、というシンプルでミニマルでありながら強力なFRPです。 27.3. エクステンション関数の実装allNoResetIO

import { None, P,//Pipe customType, customOperator, F//Function composition} from "./NonePcustomTypeOperator.js"; import { IO, next } from "./reactive-monad.js"; const identity = <A>(a: A) => a;const right = <A>(a: A) => <B>(b: B) => b; type flag = [IO<unknown>, IO<number>]; const allNoResetIO = (As: IO<any>[]): IO<unknown> => IO(None)['>'] ((result: IO<unknown>) => right (P(As.map((A: IO<unknown>) => [A, IO(0)] as flag))['>'] ((flags: flag[]) => flags.map ((flag: flag) => flag[0]['>='](//reactive A () => right (flag[1]['>'](next(1))) ((checkFlags(As)(result)(flags))) ) ) ) ) (result) ); const checkFlags = (As: IO<unknown>[]) => (result: IO<unknown>) => (flags: flag[]): any => (flags .map( (flag: flag) => flag[1].lastVal) .reduce((a, b) => a * b) === 1) //all flags are 1 && // None is not accepted to fill the result !(As.map((A: IO<unknown>) => A.lastVal) .includes(None)) ? result['>'](next( // return As lastVals As.map((A: IO<unknown>) => A.lastVal) )) : None;　export { allNoResetIO }

　allAndResetIO

import { None, P,//Pipe customType, customOperator, F//Function composition} from "./NonePcustomTypeOperator.js"; import { IO, next } from "./reactive-monad.js"; const identity = <A>(a: A) => a;const right = <A>(a: A) => <B>(b: B) => b; type flag = [IO<unknown>, IO<number>]; const allAndResetIO = (As: IO<any>[]): IO<unknown> => IO(None)['>'] ((result: IO<unknown>) => right (P(As.map((A: IO<unknown>) => [A, IO(0)] as flag))['>'] ((flags: flag[]) => flags.map ((flag: flag) => flag[0]['>='](//reactive A () => right (flag[1]['>'](next(1))) ((checkFlags(As)(result)(flags))) ) ) ) ) (result) ); const checkFlags = (As: IO<unknown>[]) => (result: IO<unknown>) => (flags: flag[]): any => (flags .map( (flag: flag) => flag[1].lastVal) .reduce((a, b) => a * b) === 1) //all flags are 1 && // None is not accepted to fill the result !(As.map((A: IO<unknown>) => A.lastVal).includes(None)) ? right (//reset all flags to 0 flags .map((flag: flag) => flag[1]['>'](next(0))) )( // return As lastVals result['>'](next( As.map((A: IO<unknown>) => A.lastVal) )) ) : None; export { allAndResetIO }

28. ReactのためのFRP（ReactiveMonad）のDemo その他

CodeSandbox上にUPしたDemoを外部ページに埋め込んで掲載しています。 関数型プログラミングが『銀の弾丸』であるという非常識な常識2022 Demo 最初のコードについてだけ解説します。

import { P } from "./NonePcustomTypeOperator.js";import { IO } from "./reactive-monad.js"; window.run = () => { const right = (a) => (b) => b; const log = (a) => right(console.log(a))(a); const pipe = P("Hello Pipe")[">"](log); // Hello Pipe const io = IO("Hello IO")[">="](log); // Hello IO};

• パイプライン演算子のためのP関数で実現されているパイプラインの式• ReactiveMonadのためにIO関数で実現されているFRPの式 双方ともがまったく同じ構造の式であることに注目してください。 前者は、パイプライン演算、f(x)という関数適用なので、1度きりのlogですが、後者は、FRPなので、IOのリアクティブ値に新しい値が入るたびにlogされていきます。その様子はDemoページでご覧になれます。29. MIT LicenseCopyright (c) 2021 Ken Okabe 以下に定める条件に従い、本ソフトウェアおよび関連文書のファイル（以下「ソフトウェア」）の複製を取得するすべての人に対し、ソフトウェアを無制限に扱うことを無償で許可します。これには、ソフトウェアの複製を使用、複写、変更、結合、掲載、頒布、サブライセンス、および/または販売する権利、およびソフトウェアを提供する相手に同じことを許可する権利も無制限に含まれます。 上記の著作権表示および本許諾表示を、ソフトウェアのすべての複製または重要な部分に記載するものとします。 ソフトウェアは「現状のまま」で、明示であるか暗黙であるかを問わず、何らの保証もなく提供されます。ここでいう保証とは、商品性、特定の目的への適合性、および権利非侵害についての保証も含みますが、それに限定されるものではありません。 作者または著作権者は、契約行為、不法行為、またはそれ以外であろうと、ソフトウェアに起因または関連し、あるいはソフトウェアの使用またはその他の扱いによって生じる一切の請求、損害、その他の義務について何らの責任も負わないものとします。 30. フリー／購入本書はMITライセンスにより無償で提供されていますが、フリーミアムコンテンツです。

有償版の特典 1. 本書で掲載しているコードについて、あらかじめディレクトリ構成されており、ESModules（ESM）ライブラリ群を含む、そのまま動作検証が可能なTypeScriptとJavaScriptのフルコードその他を含むGitHubのプライベートレポジトリへの個人アクセストークン（PAT）が付与されます。1. GitHubレポジトリを git clone することでWindows/Mac/Linuxのローカル環境にダウンロードでき、コードが実行できるようになります。 初心者にむけても利用方法が解説されています。2. 自身の関心事や取り組んでいるプロジェクトに役立つ関数型コード（FRP含む）を筆者がサンプルコードの実装をするリクエストが可能になります。すべてのリクエストに応じられるわけではありませんが、本書の最終目標としても、関数型プログラミングが机上の空論ではなくリアルワールドのコードとして役立つことを示す、という目的があるので、リアルワールドのサンプルコードとして本書に追加され公開されます。これはあくまでサンプルコード実装のリクエストであり、納期などがある業務委託ではないことはあらかじめご留意ください。

• 技術者としてキャリアと十分な収入があって本書で得られた知見をご自身の業務に活用しようとするプロの方々にはご購入をお願いしています。• 駆け出しの技術者あるいは社会人ではあるが、これから本格的なプロになろうとしていて、本書をプログラミングの入門に役立てようという方々についてはそのプロ版の販売価格の半額で提供いたします。• 学生、教育関係者の方々については有償版を無償で提供いたします。ある程度の身分や活動を確認可能なメールアドレスや有効なSNSアカウント等を、メール等でお知らせくだされば、有償版をお送りいたします。• ブログやQiitaなどのドキュメント共有サービスその他のSNSで本書をレビューしていただいた方については有償版を無償で提供いたします。Twitter/はてなブックマークなどの短文SNSでも問題ありませんが、ただの拡散ではなくコメントをお願いいたします。メール等でお知らせくだされば、有償版をお送りいたします。 関数型プログラミングが『銀の弾丸』であるという非常識な常識 2022販売サイト

https://tutorialbook.theshop.jp * Amazon PayとPayPal決済はWebページからの購入のみ

31. Contact　インスタフォロー/DM　シェアコメント　 mail : kentutorialbook@gmail.comInstagram : @ken.okabe Tweet